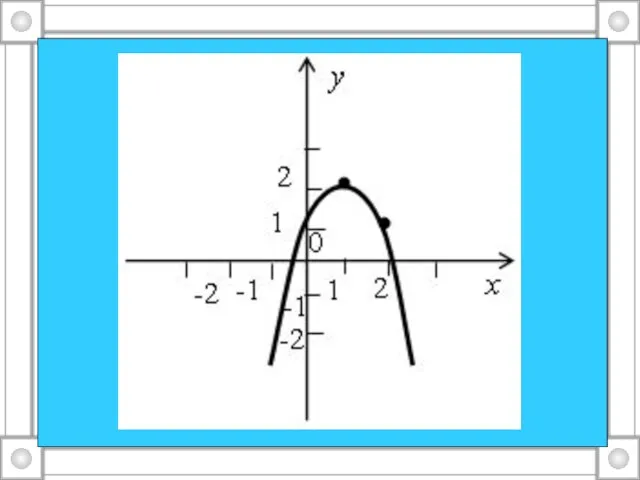
Слайд 2Определите, график какой функции изображен на рисунке:
у = х² – 2х –
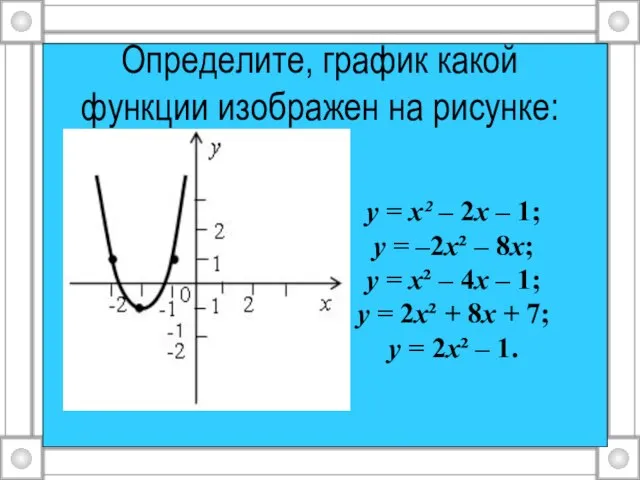
1;
у = –2х² – 8х;
у = х² – 4х – 1;
у = 2х² + 8х + 7;
у = 2х² – 1.
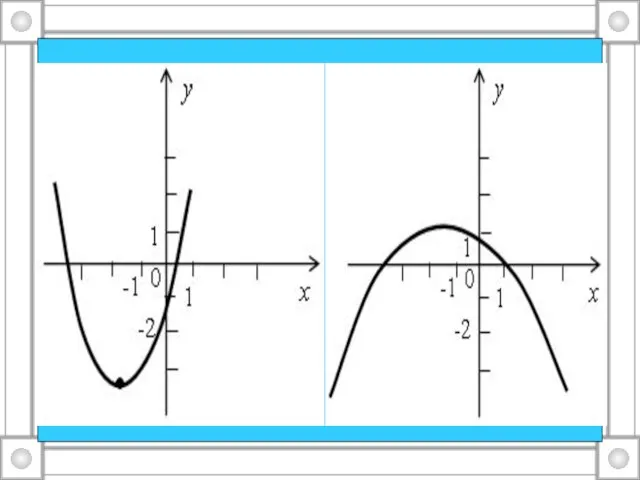
Слайд 3у = ½х² – 2х;
у = –½х² + 4х + 1;
у =
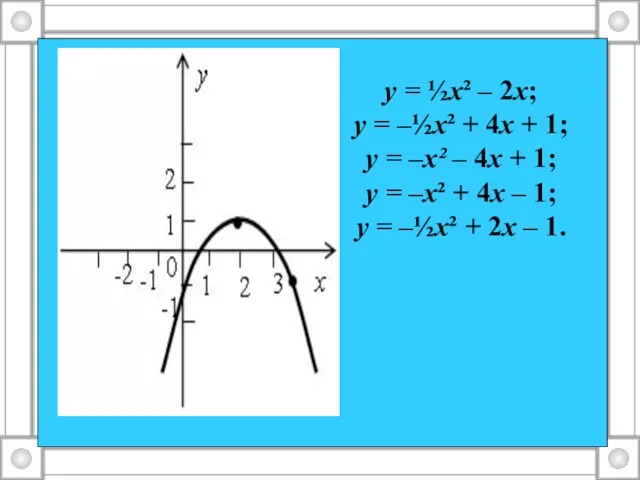
–х² – 4х + 1;
у = –х² + 4х – 1;
у = –½х² + 2х – 1.
Слайд 4 Влияние коэффициентов а, b и с на расположение графика функции у

= ах2 + bх + с.
Слайд 5Коэффициент а влияет на направление ветвей параболы:
при а > 0 –

ветви направлены вверх,
при а < 0 – вниз.
2) Коэффициент b влияет на расположение вершины параболы.
При b = 0 вершина лежит на оси ОУ.
3) Коэффициент с показывает точку пересечения параболы с осью ОУ.
Слайд 7Определите, график какой функции изображен на рисунке, опираясь на значение коэффициентов а,

b и с.
Слайд 8у = –х² + 2х;
у = ½х² + 2х + 2;
у =
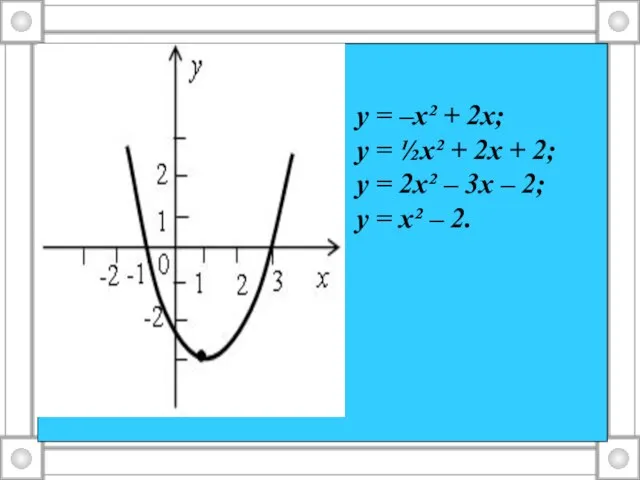
2х² – 3х – 2;
у = х² – 2.
Слайд 9у = х² – 2х;
у = –2х² + х + 3;
у =
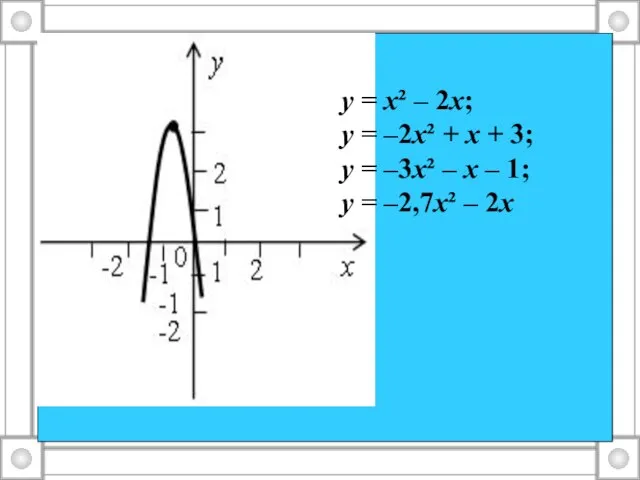
–3х² – х – 1;
у = –2,7х² – 2х
Слайд 11Итоги урока.
– Опишите алгоритм построения квадратичной функции.
– Перечислите свойства функции у

= ах2 + bх + с при а > 0 и при а < 0.
– Как влияют коэффициенты а, b и с на расположение графика квадратичной функции?








 Земноводные (2 класс)
Земноводные (2 класс) «Оскольчанка»
«Оскольчанка» Заседание ученого советаПОИПКРО
Заседание ученого советаПОИПКРО Презентация на тему Портфолио ученика (для учащихся 10-11 классов)
Презентация на тему Портфолио ученика (для учащихся 10-11 классов) What are you afraid of
What are you afraid of «Я – учитель Нашей новой школы»
«Я – учитель Нашей новой школы» Наверное, ты знаешь фильм "Кин-дза-дза". Жители планеты Кин-дза-дза обходились для всех случаев одним словом "ку". А если бы алфавит
Наверное, ты знаешь фильм "Кин-дза-дза". Жители планеты Кин-дза-дза обходились для всех случаев одним словом "ку". А если бы алфавит  SLS
SLS Экзаменационная работа
Экзаменационная работа Презентация на тему знаки препинания в конце предложения 2 класс
Презентация на тему знаки препинания в конце предложения 2 класс  Дом моей мечты
Дом моей мечты Ирина Андреевна Федосова
Ирина Андреевна Федосова Профессия Врача
Профессия Врача Satellite A110
Satellite A110 Love Story by Erich Segal
Love Story by Erich Segal  V&B_ванны до 30.04.19 0000000054
V&B_ванны до 30.04.19 0000000054 InMind: ИССЛЕДОВАНИЕ ИНТЕРНЕТ РЕСУРСОВOpinion Software Media©
InMind: ИССЛЕДОВАНИЕ ИНТЕРНЕТ РЕСУРСОВOpinion Software Media© Рыбинский полиграф колледж
Рыбинский полиграф колледж Тромбоэмболия легочной артерии
Тромбоэмболия легочной артерии Типы химических реакций
Типы химических реакций Это волшебное слово - театр
Это волшебное слово - театр Педагогический коллектив
Педагогический коллектив Модерн
Модерн Презентация на тему Географическое положение и периоды истории Древнего Египта
Презентация на тему Географическое положение и периоды истории Древнего Египта  Япония
Япония «Мама, папа, я- спортивная семья»
«Мама, папа, я- спортивная семья» Что делать если вы заблудились в тайге?
Что делать если вы заблудились в тайге? Нормализация отношений
Нормализация отношений