Параллельность прямых и плоскостей

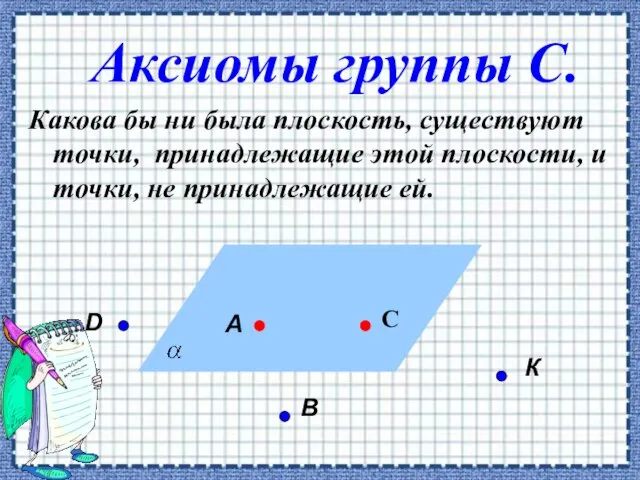
Аксиомы группы С.
Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не принадлежащие ей.
А
К
D
B
С

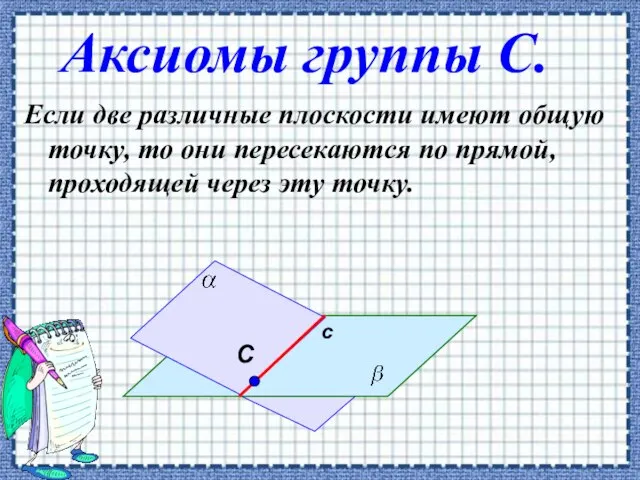
Аксиомы группы С.
Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.
С
с

Аксиомы группы С.
Если две различные прямые имеют общую точку, то через них можно провести плоскость, и притом только одну.
a
b
С

Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.

М
Следствия из аксиом
Т1

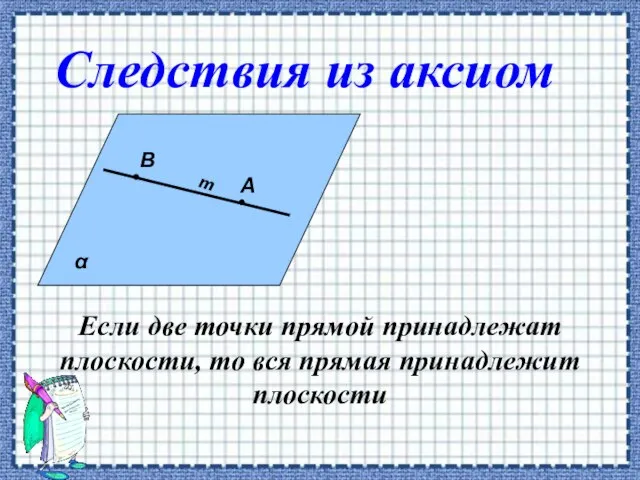
Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости

А
В
Следствия из аксиом

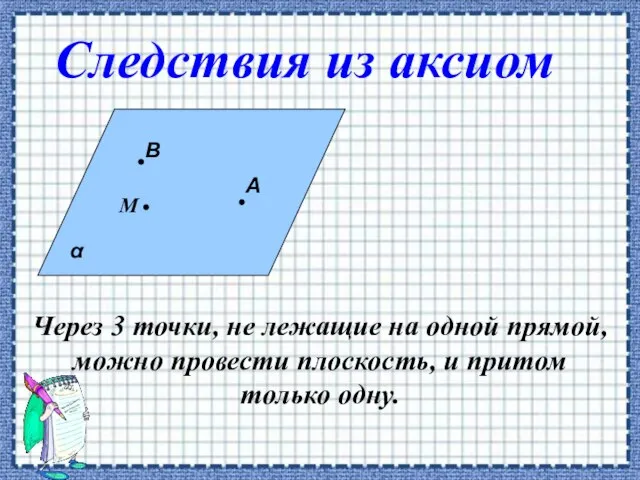
Через 3 точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

М
А
В
Следствия из аксиом

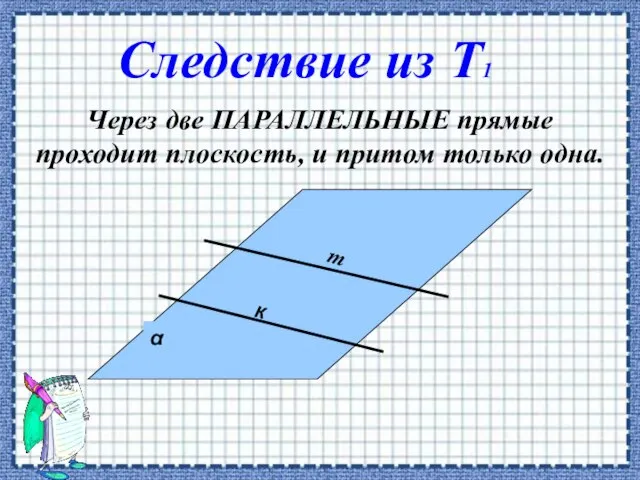
Через две ПАРАЛЛЕЛЬНЫЕ прямые проходит плоскость, и притом только одна.
к
Следствие из Т1

Вывод
Как в пространстве можно однозначно задать плоскость?
1. По трем точкам
2. По прямой и не принадлежащей ей точке.
3. По двум пересекающимся прямым.
4. По двум параллельным прямым.

Сколько существует способов задания плоскости?
Сколько плоскостей можно провести через выделенные элементы?
а)
б)
в)
г)
д)
е)
Ответьте на вопросы

Нет
Да
Нет
Да
Нет
Да
Определите: верно, ли утверждение?

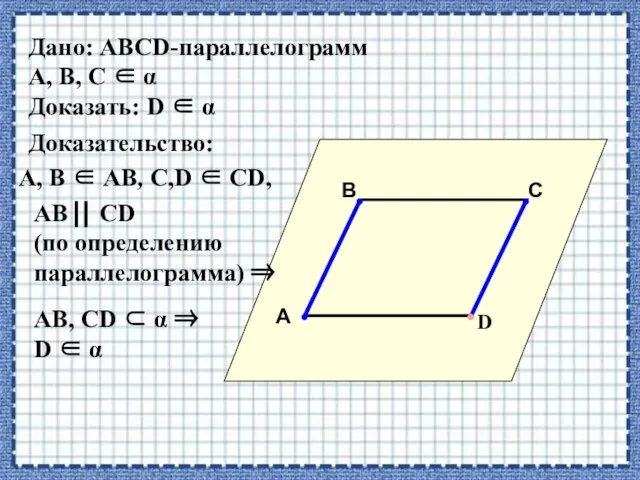
Дано: АВСD-параллелограмм
А, В, С  α
Доказать: D  α
А
В
С
D
•
•
•
•
Доказательство:
А, В  АВ, С,D  СD,
АВ  СD
(по определению параллелограмма) 
АВ, СD  α 
D  α

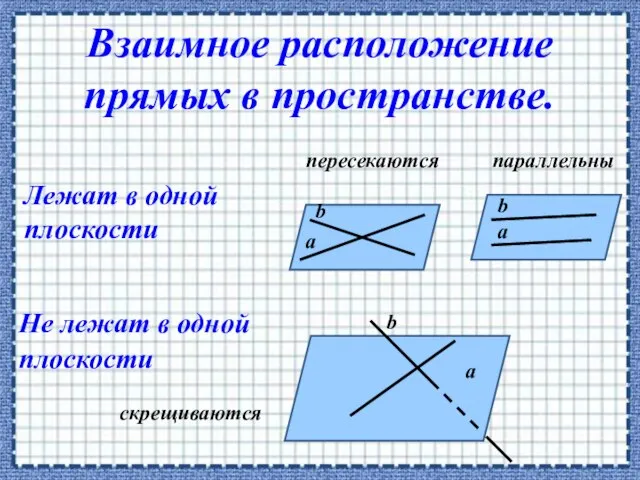
пересекаются
параллельны
а
а
а
b
b
b
скрещиваются
Лежат в одной плоскости
Не лежат в одной плоскости
Взаимное расположение прямых в пространстве.

Доказательство:
а
с
в1
в
β
α

В
1 случай. а, в, с α рассмотрен в планиметрии
2 случай. а, в  α; а, с  β
1. Возьмем т.В, В  в
Через т.В и с проведем плоскость 
  α = в1
2. Если в1  β = Х,  Х  а, в1  α,
но Х  с, т.к. в1   , а т.к. а с  в1  β
3. в1  α, в1  а  в1  а  в1 = в (А параллельных прямых)
4.  в с
Теорема доказана.
•
Две прямые, параллельные третьей прямой, параллельны

Теорема о параллельных прямых.
К
a
b
Дано: К  a
Доказать:
 ! b: К  b, b  a
Доказательство:
1.Проведем через прямую a и точку К плоскость α.
2.Проведем через т. К α прямую b, b a.(А планиметрии)
Единственность (от противного)
1.Пусть  b1: К  b1 , b1 a .Через прямые a и b1 можно провести плоскость α1.
2. a , К  α1;  α1 и α (Т о точке и прямой в пространстве).
3.  b = b1 (А параллельных прямых). Теорема доказана.

Задание 1 Вставьте пропущенные слова
Единственную плоскость можно задать через три точки, при этом они на одной прямой.
2) Если точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.
3) Две различные плоскости могут иметь только одну общую
4) Прямые являются в пространстве, если они не пересекаются и в одной плоскости.
5) Если прямая a лежит в плоскости α, прямая b не лежит в плоскости α, но пересекает ее в точке
В
α, то прямые а и b
не лежат
две
прямую
параллельными
лежат
скрещивающиеся

Задание 2 Определите: верно, ли утверждение?
Нет
Нет
Да
Да
Нет

Задание 2 Определите: верно, ли утверждение?
Нет
Нет
Нет
Да

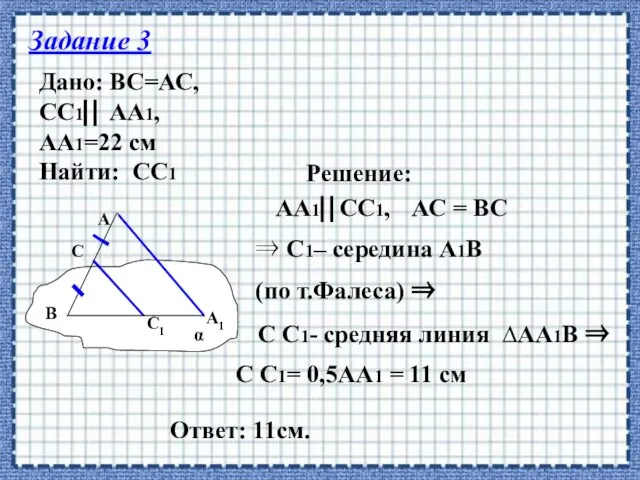
Задание 3
Дано: ВС=АС,
СС1 АА1,
АА1=22 см
Найти: СС1
Решение:
АА1СС1,
АС = ВС
 С1– середина А1В
(по т.Фалеса) 
С С1- средняя линия ∆АА1В 
С С1= 0,5АА1 = 11 см
Ответ: 11см.

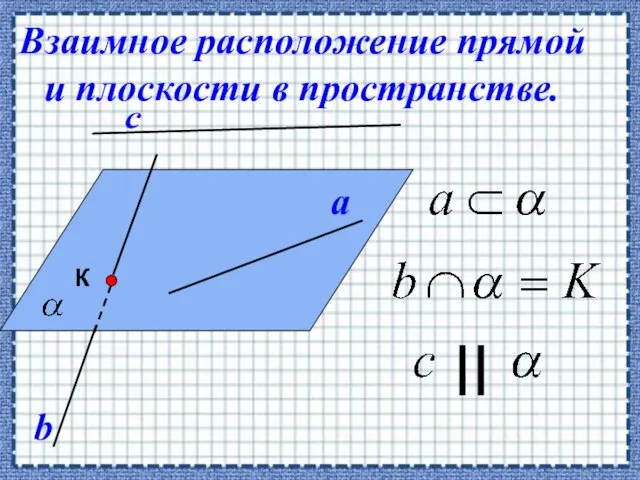
Взаимное расположение прямой и плоскости в пространстве.

Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой,
лежащей в этой плоскости , то
она параллельна и самой плоскости.
Дано:
Доказать:

1.Через прямые a и b проведем плоскость α
Пусть , , α
2. α  β = b
Если a  β = Х, то Х  b, это невозможно, т.к. α  b
 a  β
 a  β
Теорема доказана.

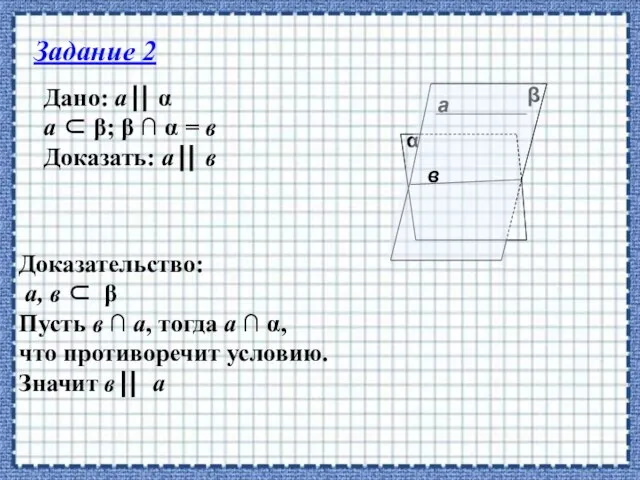
Дано: а  α
а  β; β ∩ α = в
Доказать: а  в
Доказательство:
а, в  β
Пусть в ∩ а, тогда а ∩ α,
что противоречит условию.
Значит в  а
Задание 2
α
β
а
в

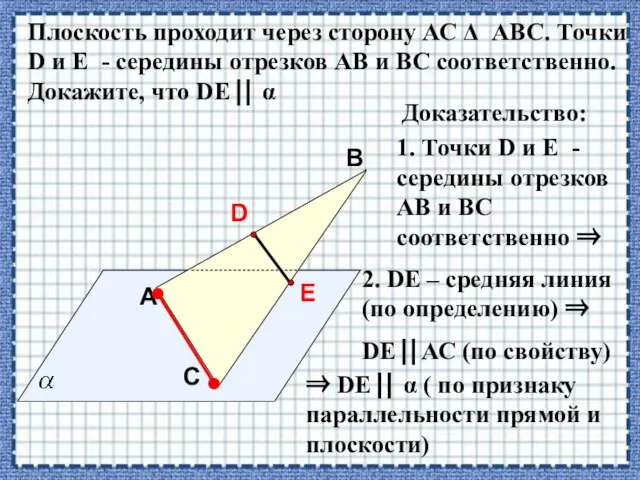
A
В
С
Плоскость проходит через сторону АС  АВС. Точки D и E - середины отрезков АВ и BC соответственно. Докажите, что DE  α
Доказательство:
1. Точки D и E - середины отрезков АВ и BC соответственно 
2. DE – средняя линия (по определению) 
DE АС (по свойству)
 DE  α ( по признаку параллельности прямой и плоскости)

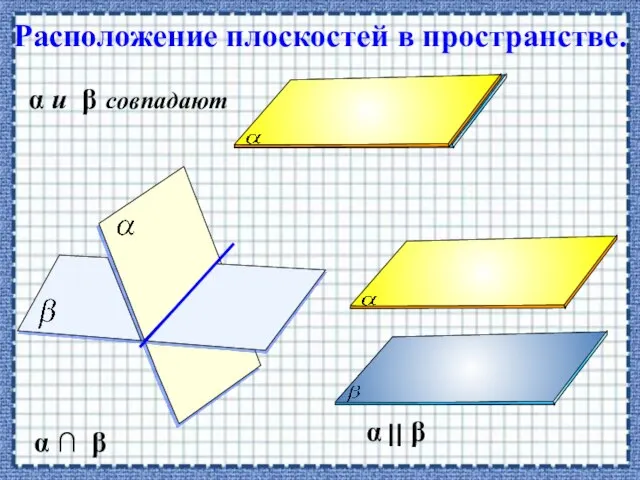
Расположение плоскостей в пространстве.
α  β
α и β совпадают
α  β

Признак параллельности двух плоскостей.
Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
пересекающимся прямым другой плоскости, то эти
плоскости параллельны.
Дано: а b = M, a , b .
a₁ b₁, a₁ , b₁ . a  a₁, b  b₁.
Доказать:  


а
а₁
b
b₁
M
c
Доказательство:
Тогда а  , а  ,    = с, значит а  с.
2. b  , b  ,    = с, значит b  с.
3. Имеем, что через точку М проходят две прямые а и b, параллельные прямой с, чего быть на может.
Значит    .
1. Пусть    = с.

Теорема
Через точку вне данной плоскости можно провести плоскость, параллельную данной, причём единственную.
β
а1
•
А
α
плоскость α,
в1
в
а
Доказать:
Доказательство.
Дано:
точка А вне плоскости α.
существует плоскость β║α, проходящая через точку А
1. В плоскости α проведём прямые а∩в.
Через точку А проведём
а1║а
и в1║в.
По признаку параллельности плоскостей прямые а1 и в1 задают плоскость β║α.
Существование плоскости β доказано.

β
•
А
α
Докажем единственность плоскости β методом от противного.
•
С
•
В
в
с
β1

Допустим, что существует плоскость β1, которая проходит через т. А и β1  α.
Отметим в плоскости β1 т. С β.
Отметим произвольную т. В  α.
Через точки А, В и С проведем γ.
γ ∩ α = в,
γ ∩ β1 = с.
γ ∩ β = а,
а
а и с не пересекают плоскость α,
значит они не пересекают прямую в,
 а  в и с  в
Получили, что через т. А проходят две прямые, параллельные прямой в, чего быть не может.
 наше предположение ложное.
Единственность β доказана.

Если две параллельные плоскости
пересечены третьей, то линии их пересечения параллельны.
Свойство параллельных плоскостей.
Дано:
α  β, α   = a
β   = b
Доказать: a  b
Доказательство:
1. a  , b  
2. Пусть a  b,
тогда a  b = М
3. M  α, M  β
 α  β = с (А2)
Получили противоречие с условием.
Значит a  b ч. т.д.

Отрезки параллельных прямых,
заключенные между параллельными
плоскостями, равны.
Свойство параллельных плоскостей.
Доказать: АВ = СD
Дано:
α  β, АВ СD
АВ  α = А, АВ  β = В,
СD  α = С, СD  β = D
Доказательство:
1. Через АВ СD проведем 
2. α β, α   = a, β   = b
3.  АС В D,
4. АВ СD (как отрезки парал. прямых)
5.  АВСД – параллелограмм (по опр.)
 АВ = СD ( по свойству параллелограмма)

1. если плоскости не пересекаются, то они параллельны.
2. плоскости параллельны, если прямая лежащая в
одной плоскости, параллельна другой плоскости?
3. если две прямые, лежащие в одной плоскости, параллельны двум прямым другой плоскости,
то эти плоскости параллельны?
4. если прямая перпендикулярна одной из двух параллельных плоскостей, то она
перпендикулярна и другой плоскости.
5. прямые, по которым две параллельные плоскости пересечены третьей плоскостью, параллельны.
6. Если прямая пересекает одну из двух плоскостей, то
она пересекает и другую.
7. Две плоскости, параллельные третьей, параллельны.
8. Отрезки прямых, заключенные между
параллельными плоскостями, равны.
Определите: верно, ли утверждение?
ДА
НЕТ
ДА
НЕТ
ДА
НЕТ
НЕТ
ДА

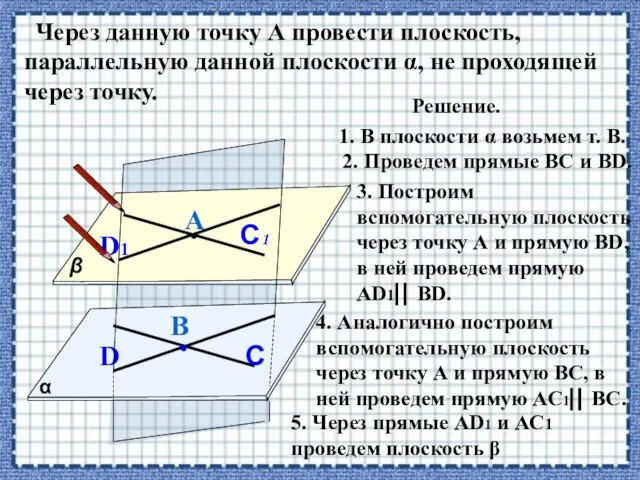
Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку.
α
β
А
Решение.
1. В плоскости α возьмем т. В.
2. Проведем прямые ВС и ВD.
В
•
С1
D1
D
С
3. Построим вспомогательную плоскость через точку А и прямую ВD, в ней проведем прямую АD1 ВD.
4. Аналогично построим вспомогательную плоскость через точку А и прямую ВС, в ней проведем прямую АС1 ВС.
•
5. Через прямые АD1 и АС1 проведем плоскость β

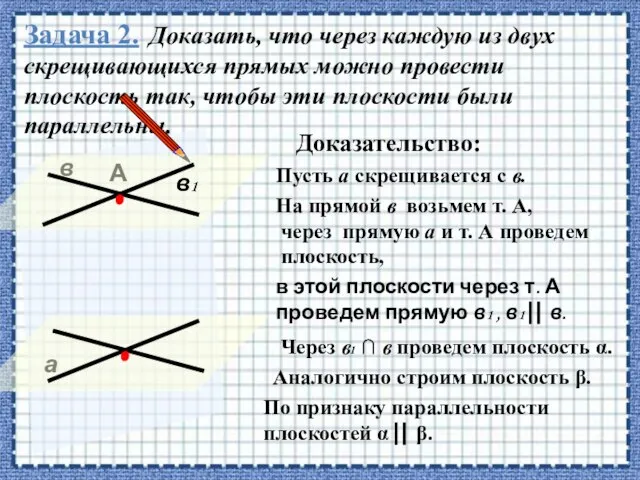
Задача 2. Доказать, что через каждую из двух скрещивающихся прямых можно провести плоскость так, чтобы эти плоскости были параллельны.
а
в
Пусть а скрещивается с в.
Доказательство:
На прямой в возьмем т. А,
А
через прямую а и т. А проведем плоскость,
в этой плоскости через т. А проведем прямую в1 , в1  в.
Через в1  в проведем плоскость α.
.
в1
Аналогично строим плоскость β.
По признаку параллельности плоскостей α  β.
.