Содержание
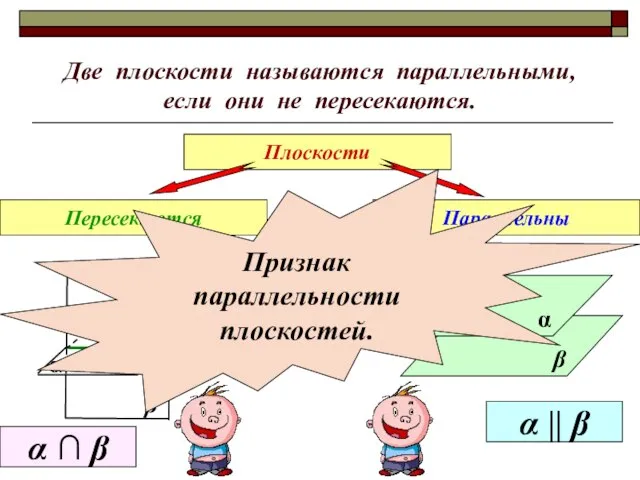
- 2. Две плоскости называются параллельными, если они не пересекаются. Плоскости Пересекаются Параллельны β α α || β
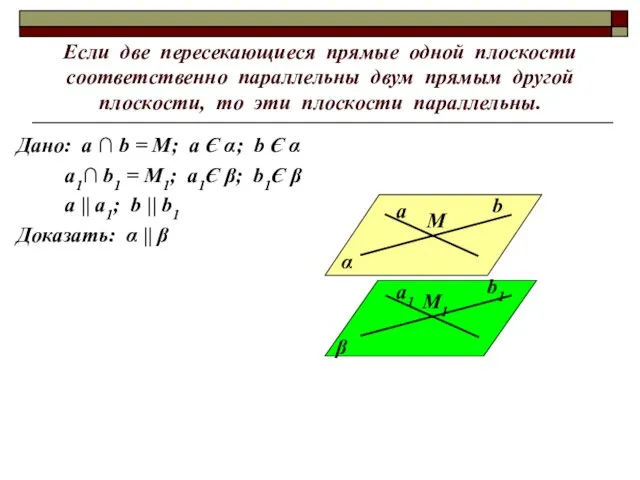
- 3. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
- 4. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
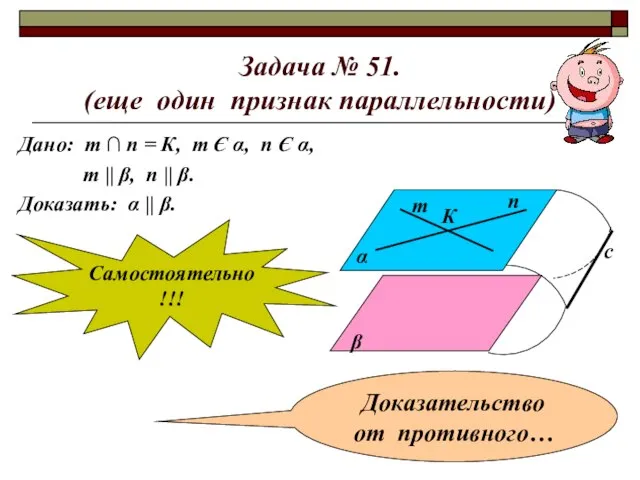
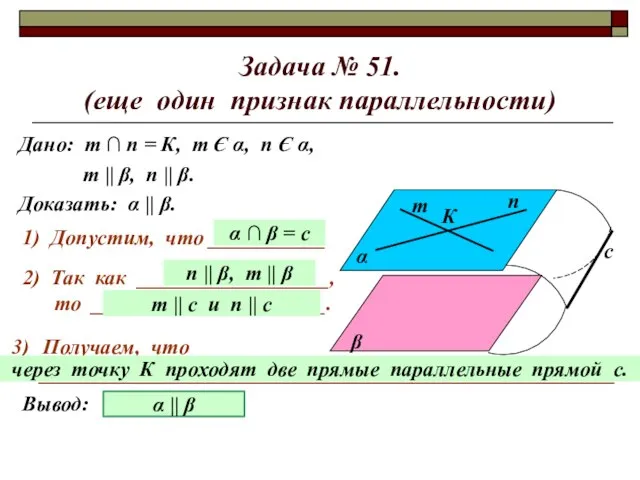
- 5. Задача № 51. (еще один признак параллельности) Дано: т ∩ п = К, т Є α,
- 6. Задача № 51. (еще один признак параллельности) Дано: т ∩ п = К, т Є α,
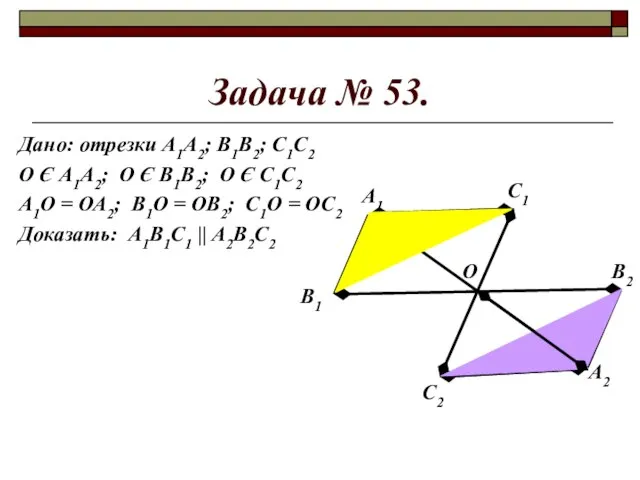
- 7. Задача № 53. Дано: отрезки А1А2; В1В2; С1С2 О Є А1А2; О Є В1В2; О Є
- 8. Задача № 53. Дано: отрезки А1А2; В1В2; С1С2 О Є А1А2; О Є В1В2; О Є
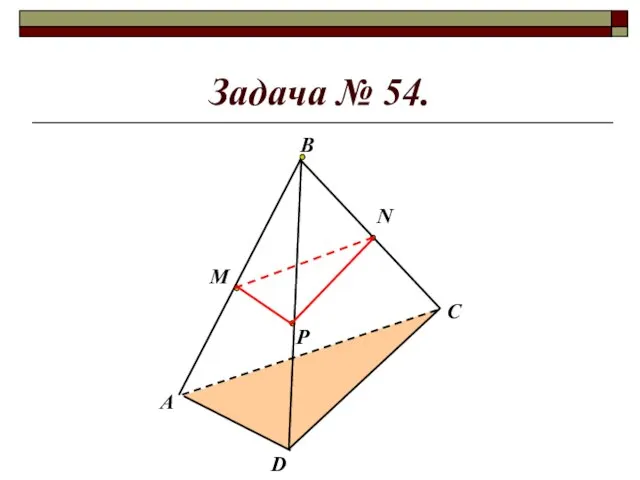
- 9. Задача № 54. М Р N А В D C
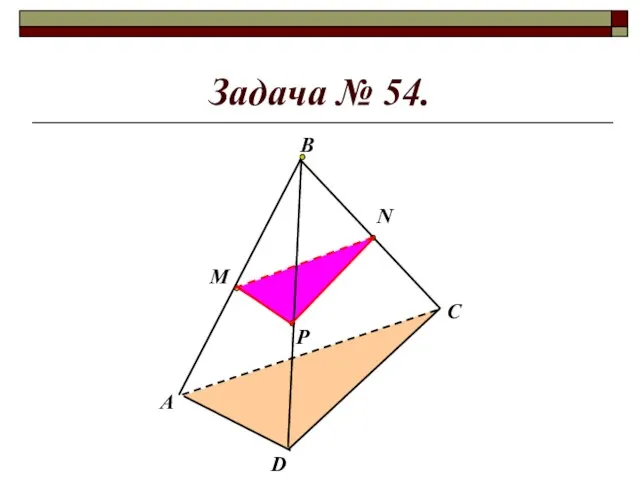
- 10. Задача № 54. М Р N А D C В
- 11. Ответьте на вопросы: Могут ли прямая и плоскость не иметь общих точек? Верно ли, что если
- 13. Скачать презентацию



 Занятие 1
Занятие 1 Пролегомены к теории языка
Пролегомены к теории языка Метод проектов в работе учителя
Метод проектов в работе учителя Искусство и власть: их влияние друг на друга и взаимодействие
Искусство и власть: их влияние друг на друга и взаимодействие Орфографическая диктовка
Орфографическая диктовка "О вреде курения"
"О вреде курения" Изменения 2012 в трудовом законодательстве
Изменения 2012 в трудовом законодательстве Россия в XVII веке
Россия в XVII веке Что_будет_с_рынком_недвижимости_часть_2
Что_будет_с_рынком_недвижимости_часть_2 Ваш текст. Шаблон
Ваш текст. Шаблон Покрытия Caparol для промышленных полов со специальными требованиями
Покрытия Caparol для промышленных полов со специальными требованиями ПРЕЗЕНТАЦИЯ ПО ПСИХОЛОГИИ
ПРЕЗЕНТАЦИЯ ПО ПСИХОЛОГИИ ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕНЛИТЕРАТУРА2 часть
ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕНЛИТЕРАТУРА2 часть Создание мультимедийных презентаций
Создание мультимедийных презентаций Стиль Luxe purism
Стиль Luxe purism Живые существа. Группы живых существ (3 класс)
Живые существа. Группы живых существ (3 класс) Макроэкономическая политика
Макроэкономическая политика Белорусская жемчужина в коллекции Козелл-Поклевских
Белорусская жемчужина в коллекции Козелл-Поклевских Организация деятельности социально-педагогического и медико-психологического центра на основе народных традиций
Организация деятельности социально-педагогического и медико-психологического центра на основе народных традиций Презентация на тему Подтип Позвоночные Рыбы
Презентация на тему Подтип Позвоночные Рыбы  Семантика орнаментальных узоров ханты и манси
Семантика орнаментальных узоров ханты и манси HYDE PARK
HYDE PARK Тамбовский вклад в русскую культуру в первой половине 19 века
Тамбовский вклад в русскую культуру в первой половине 19 века Краткая информация по рынку агрострахования в 2010 годуwww.agroins.com.ua Ирина ГринюкЗаместитель руководителя Проекта“Развитие агро
Краткая информация по рынку агрострахования в 2010 годуwww.agroins.com.ua Ирина ГринюкЗаместитель руководителя Проекта“Развитие агро Творческий проект «Сердце из роз»
Творческий проект «Сердце из роз» Классный час «Поговорим о доброте»
Классный час «Поговорим о доброте» Бизнес-симулятор
Бизнес-симулятор Портфолио – профессиональный портрет библиотекаря образовательного учреждения
Портфолио – профессиональный портрет библиотекаря образовательного учреждения