Содержание
- 2. Параметрическое линейное программирование представляет собой один из разделов математического программирования, изучающий задачи, в которых целевая функция
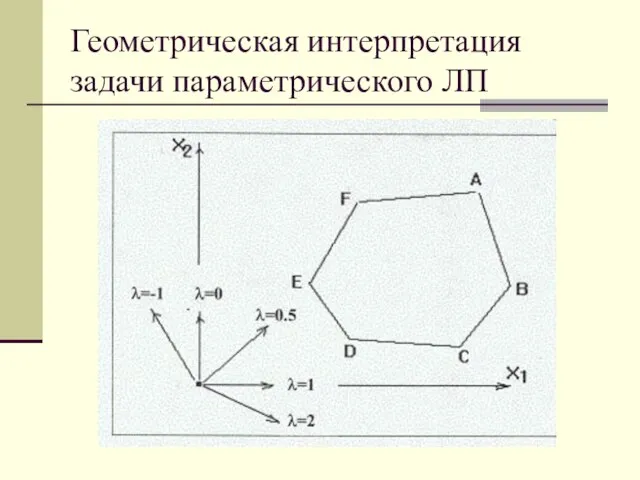
- 3. Геометрическая интерпретация задачи параметрического ЛП Если обратиться к геометрической интерпретации задачи, то можно заметить, что вектор-градиент
- 4. Геометрическая интерпретация задачи параметрического ЛП
- 5. Алгоритм решения задачи параметрического ЛП Считая значение параметра равным некоторому числу , находим оптимальный план Х*
- 6. Пример задачи параметрического ЛП Предприятие должно выпустить два вида продукции А и В, для изготовления которых
- 7. Решение задачи: Строим систему ограничений, находим целевую функцию:
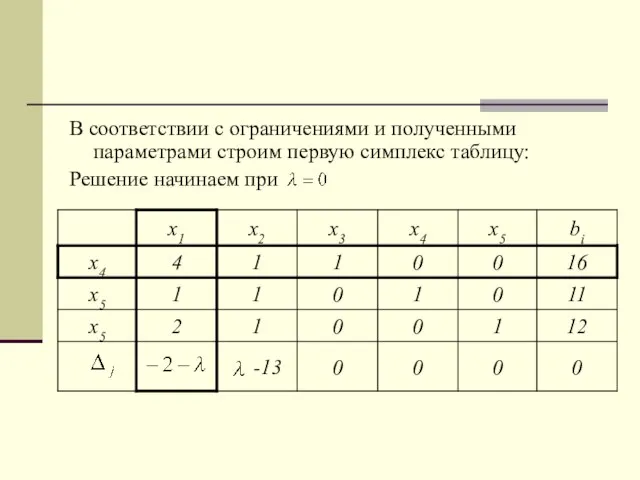
- 8. В соответствии с ограничениями и полученными параметрами строим первую симплекс таблицу: Решение начинаем при
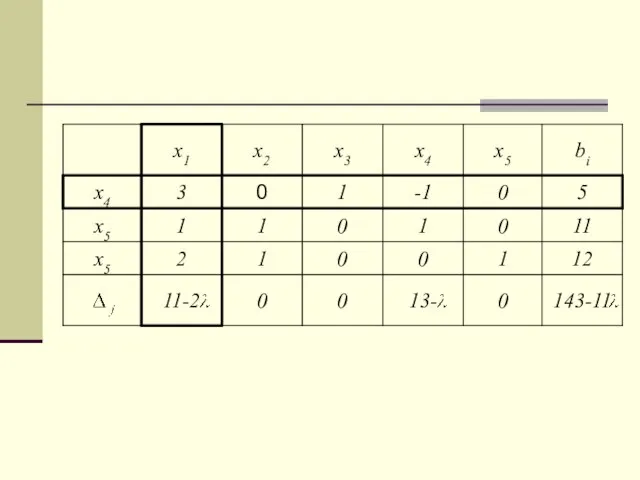
- 10. При решение найдено. Найдем интервал изменения , при котором решение будет оставаться оптимальным. При > выбранный
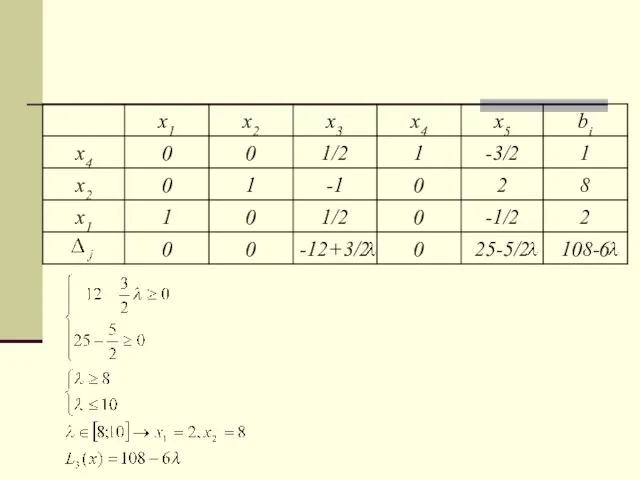
- 12. Ищем решение при
- 15. Скачать презентацию








 Презентация на тему Основные инфекционные заболевания и их профилактика
Презентация на тему Основные инфекционные заболевания и их профилактика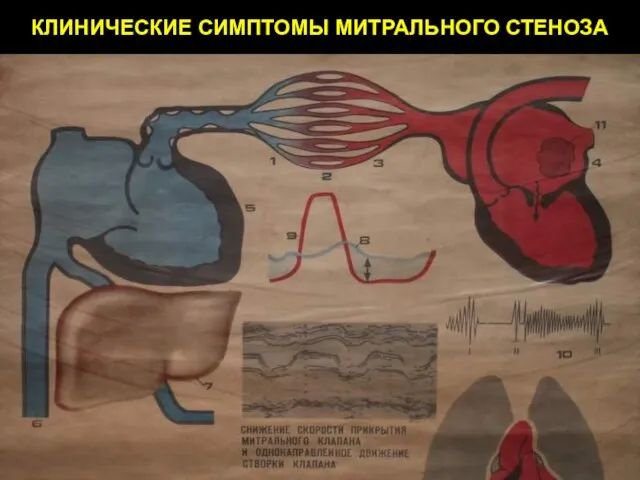 Митральные пороки
Митральные пороки  Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости
Влияние компьютерных игр на здоровье младших школьников и определение компьютерной зависимости Презентация на тему Пальчиковая гимнастика
Презентация на тему Пальчиковая гимнастика  “Мастерская для инноваций”
“Мастерская для инноваций” В каких странах говорят на английском языке?
В каких странах говорят на английском языке? В ожидании Рождества. Фотоальбом
В ожидании Рождества. Фотоальбом В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:
В.Б. Тарасов МГТУ им. Н.Э.Баумана, Кафедра «Компьютерные системы автоматизации производства» e-mail:  Административная ответственность
Административная ответственность МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,
МЕХАНИЗМЫ ВЗАИМОДЕЙСТВИЯ ВЕРБАЛЬНЫХ И НЕВЕРБАЛЬНЫХ ЕДИНИЦ В ДИАЛОГЕ II Б. ДЕЙКТИЧЕСКИЕ ЖЕСТЫ И РЕЧЕВЫЕ АКТЫ Крейдлин Г. Е. (РГГУ,  Технология как часть общечеловеческой культуры
Технология как часть общечеловеческой культуры Коммуникационные технологии
Коммуникационные технологии  Атмосфера: значение, строение, изучение
Атмосфера: значение, строение, изучение Презентация на тему Вода в природе 3 класс
Презентация на тему Вода в природе 3 класс  Презентация на тему Фалес Милетский
Презентация на тему Фалес Милетский Реки
Реки Блинчики-Мск. Проект
Блинчики-Мск. Проект Презентация на тему Чтобы путь был счастливым (3 класс)
Презентация на тему Чтобы путь был счастливым (3 класс) Развитие социальной психологии
Развитие социальной психологии проект ккт
проект ккт Установка коннектора компрессора на новых корейских компрессорах!
Установка коннектора компрессора на новых корейских компрессорах! Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ
Я РАДА ПРИВЕТСТВОВАТЬ ВАС НА УРОКЕ ФИЗИКИ общая характеристика растений
общая характеристика растений Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация
Новогодний хороводНам очень веселоВозьмёмся за руки.. - презентация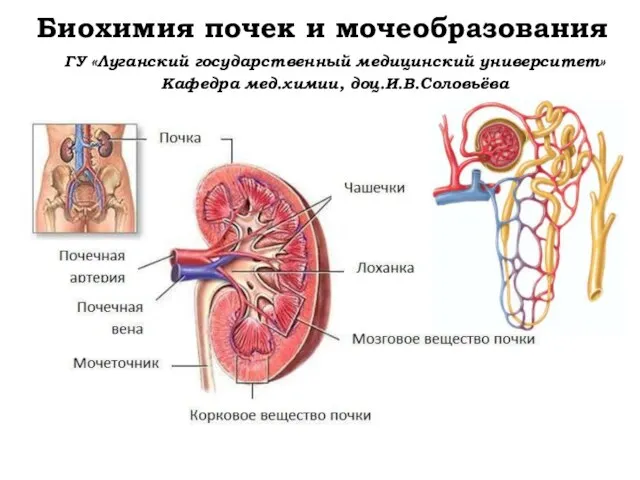 Биохимия почек и мочеобразования
Биохимия почек и мочеобразования Сертификация систем качества
Сертификация систем качества Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы
Презентация на тему Экологические факторы. Антропогенное воздействие на экосистемы Птичья азбука
Птичья азбука