Пересечение линии и поверхности

Линия и поверхность пересекаются в одной или нескольких точках.
Точки пересечения линии и поверхности принадлежат одновременно обеим фигурам.
Если одна из пересекающихся фигур - проецирующая, то проекция точки пересечения фигур принадлежит следу проецирующей фигуры, вторую проекцию точки строят из условия ее принадлежности непроецирующей фигуре

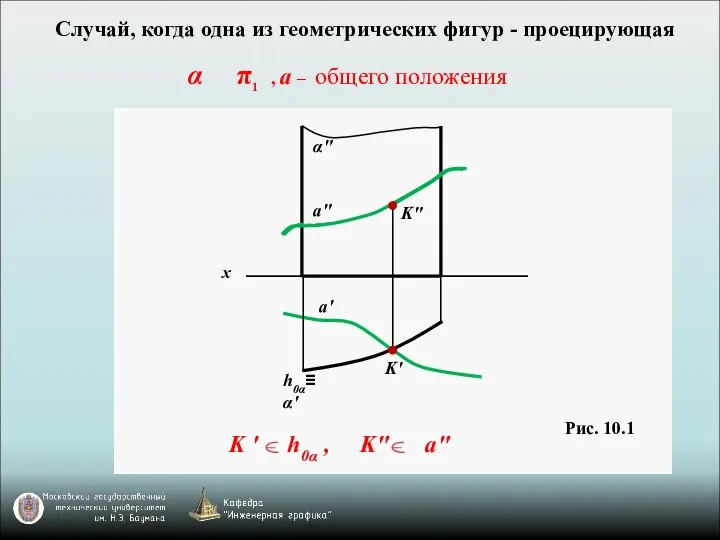
Случай, когда одна из геометрических фигур - проецирующая
α π1 , а – общего положения
Рис. 10.1
K ' h0α , K" а"
K"
a"
α"
x
K'
a'
h0α≡ α'

Случай, когда одна из геометрических фигур - проецирующая
а π1 , α - общего положения
Рис. 10.2
K '≡ а' , K" α"
l'
≡ K'
α'
x
K"
l"
α"
a'
a"

Случай, когда обе геометрические фигуры – общего положения
Алгоритм решения:
Заключить линию а во вспомогательную поверхность ϒ
Построить линию l пересечения вспомогательной поверхности ϒ с заданной поверхностью
Отметить искомую точку К на пересечении заданной линии а с построенной линией l
Рис. 10.3

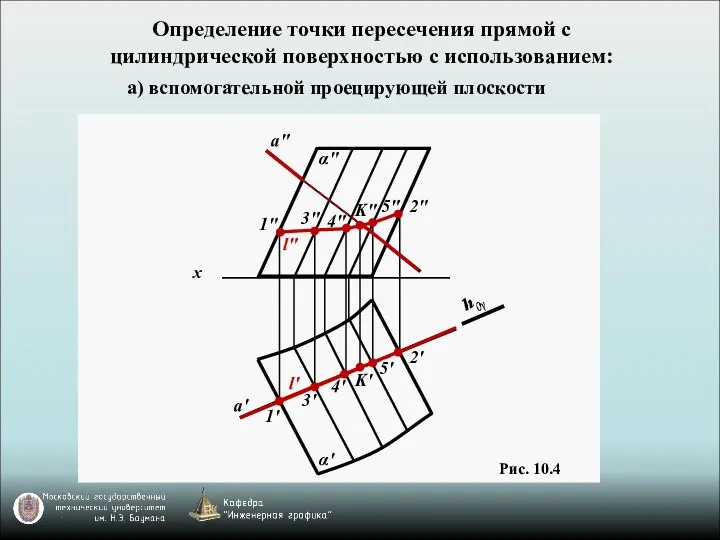
Определение точки пересечения прямой с цилиндрической поверхностью с использованием:
а) вспомогательной проецирующей плоскости
Рис. 10.4
K"
1"
2"
3"
a"
α"
x
α'
2'
K'
a'
1'
3'
h0γ
l'
l"
4'
5'
4"
5"

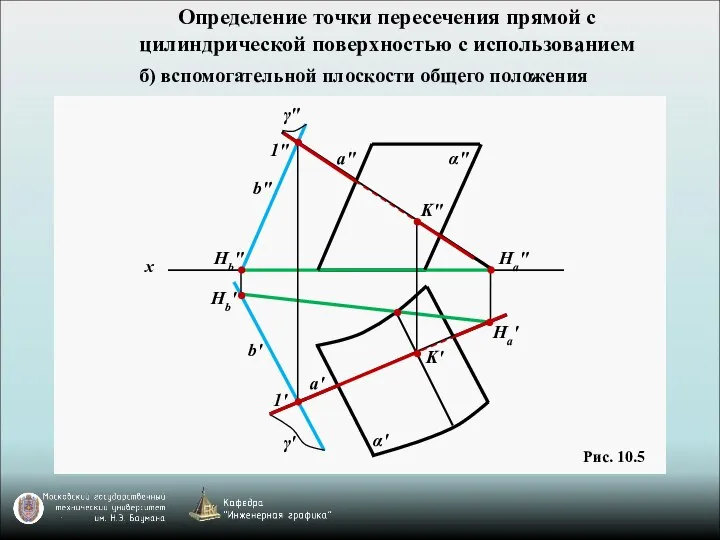
Определение точки пересечения прямой с цилиндрической поверхностью с использованием
б) вспомогательной плоскости общего положения
Рис. 10.5
1"
b"
α"
K"
Hb"
Ha"
x
γ"
a'
b'
α'
K'
γ'
1'
Ha'
Hb'
a"

Касательная плоскость
и
нормаль к поверхности
Горячкина А.Ю.

Рис. 9.1
Плоскость, касательная к поверхности в заданной точке – есть множество касательных, проведенных к поверхности через заданную точку
Касательная t к поверхности – прямая, касательная к какой-либо линии, принадлежащей поверхности
Нормаль n к поверхности в заданной точке – перпендикуляр к касательной плоскости к поверхности в заданной точке
Линию пересечения поверхности с плоскостью, проходящей через нормаль, называют нормальным сечением

Задание плоскости, касательной к поверхности в заданной точке
Т.к. плоскость определяется двумя пересекающимися прямыми, то для задания плоскости, касательной к поверхности в заданной точке, проводят две линии, принадлежащие поверхности и к ним строят касательные
Алгоритм построения плоскости,
касательной к поверхности в точке А:
Провести линии-посредники а и в, принадлежащие поверхности,
и проходящие через точку А (линии-посредники на данной поверхности следует выбирать так, чтобы они проецировались как простейшие (прямые, окружности)
Построить прямые t1 и t2 , касательные к линиям а и в в точке А
3. Плоскость τ , заданная прямыми t1 и t2 , будет касательной к поверхности в заданной точке А

Рис. 9.2
Точка А – эллиптическая точка:
- касание в точке;
поверхность расположена по одну сторону от касательной плоскости
Поверхности, состоящие только из эллиптических точек, являются выпуклыми и
называются поверхностями положительной кривизны (сфера, эллипсоид, параболоид)

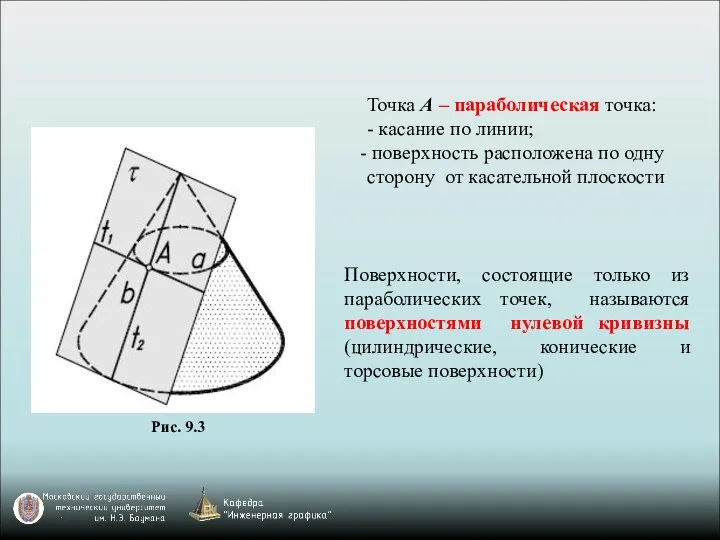
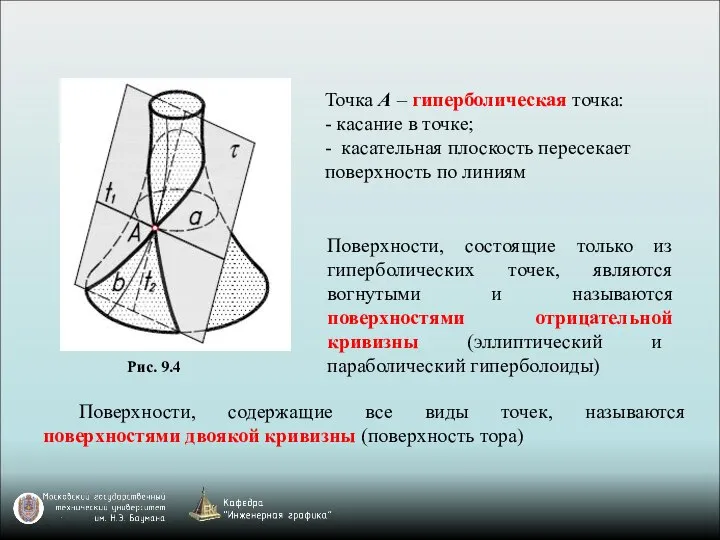
Поверхности, состоящие только из параболических точек, называются поверхностями нулевой кривизны (цилиндрические, конические и торсовые поверхности)
Точка А – параболическая точка:
- касание по линии;
поверхность расположена по одну сторону от касательной плоскости
Рис. 9.3

Точка А – гиперболическая точка:
- касание в точке;
- касательная плоскость пересекает поверхность по линиям
Поверхности, состоящие только из гиперболических точек, являются вогнутыми и называются поверхностями отрицательной кривизны (эллиптический и параболический гиперболоиды)
Поверхности, содержащие все виды точек, называются поверхностями двоякой кривизны (поверхность тора)
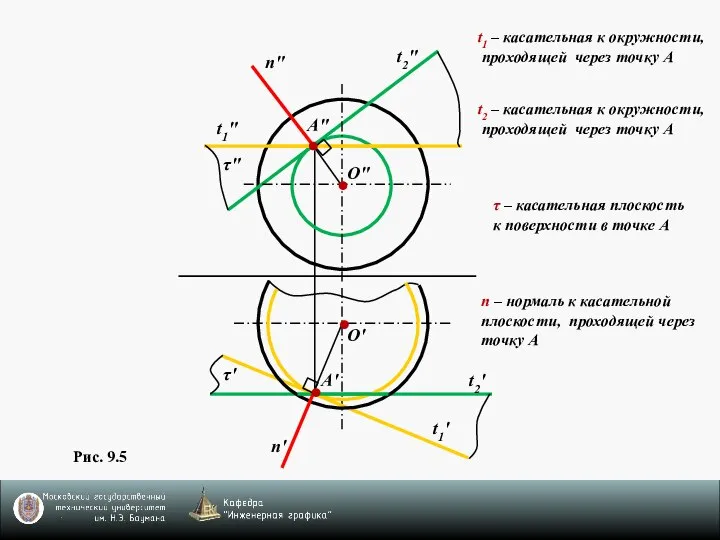
Рис. 9.4

Рис. 9.5
t1'
n'
O'
A'
t2'
O"
A"
n"
t1"
t2"
n – нормаль к касательной плоскости, проходящей через
точку А
t1 – касательная к окружности,
проходящей через точку А
t2 – касательная к окружности,
проходящей через точку А
τ – касательная плоскость
к поверхности в точке А
τ'
τ"

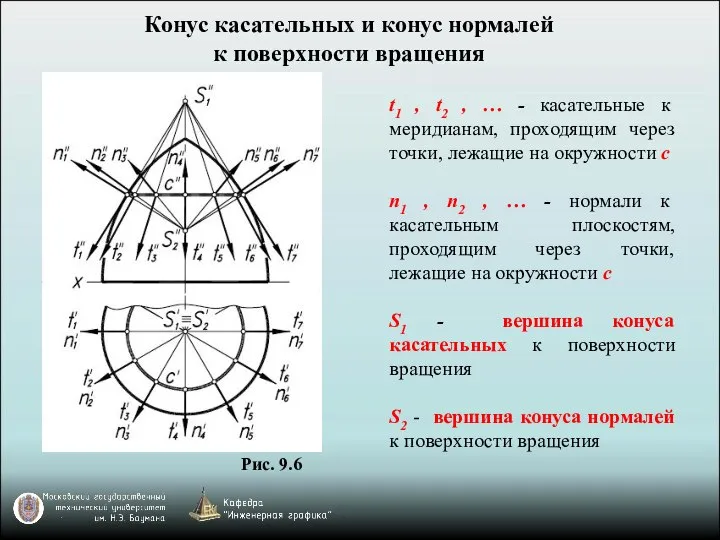
Рис. 9.6
Конус касательных и конус нормалей
к поверхности вращения
t1 , t2 , … - касательные к меридианам, проходящим через точки, лежащие на окружности с
п1 , n2 , … - нормали к касательным плоскостям, проходящим через точки, лежащие на окружности с
S1 - вершина конуса касательных к поверхности вращения
S2 - вершина конуса нормалей к поверхности вращения