Содержание
- 2. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) метод сфер-посредников (способ вспомогательных секущих сфер)
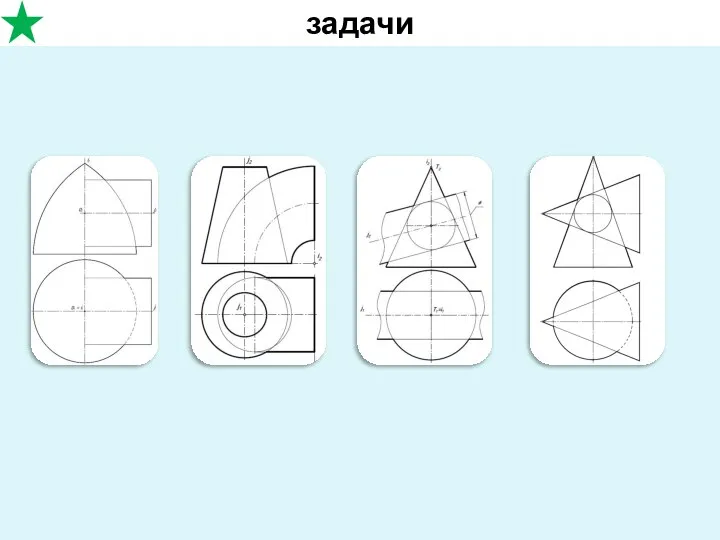
- 3. задачи
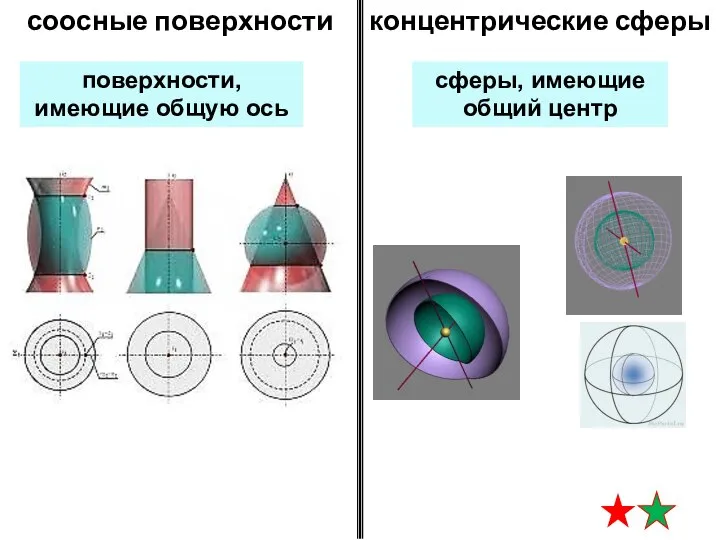
- 4. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
- 5. сферы, имеющие общий центр концентрические сферы соосные поверхности поверхности, имеющие общую ось
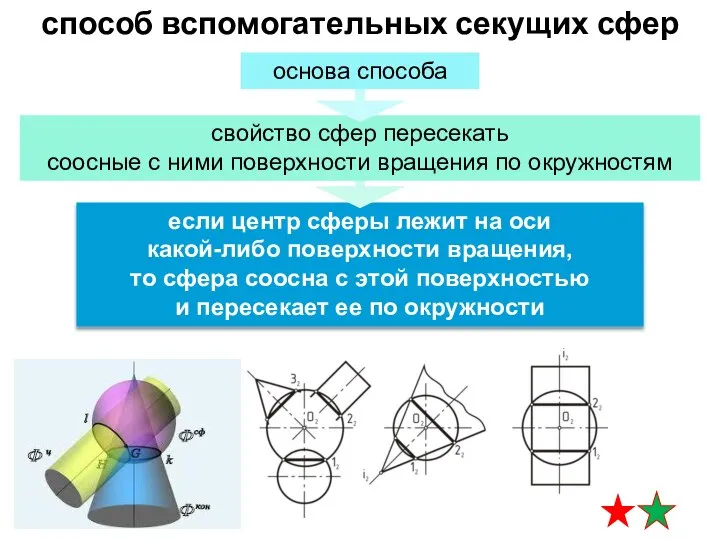
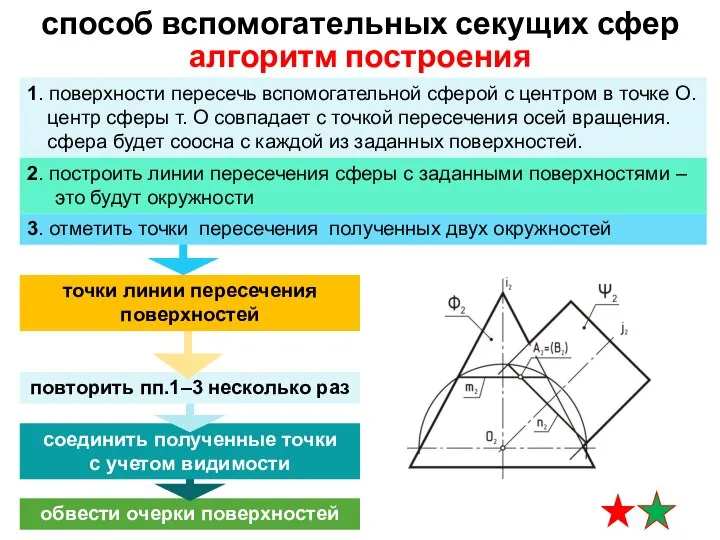
- 6. способ вспомогательных секущих сфер если центр сферы лежит на оси какой-либо поверхности вращения, то сфера соосна
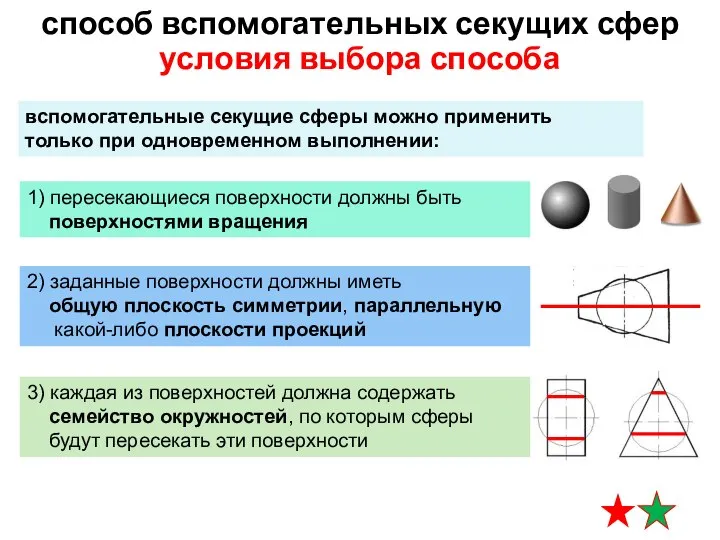
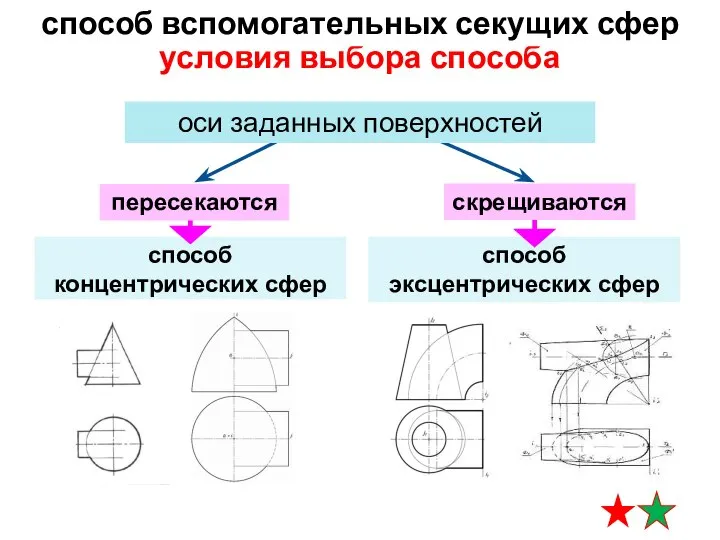
- 7. вспомогательные секущие сферы можно применить только при одновременном выполнении: условия выбора способа способ вспомогательных секущих сфер
- 8. способ эксцентрических сфер способ концентрических сфер условия выбора способа способ вспомогательных секущих сфер пересекаются скрещиваются оси
- 9. обвести очерки поверхностей соединить полученные точки с учетом видимости повторить пп.1–3 несколько раз алгоритм построения способ
- 10. содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
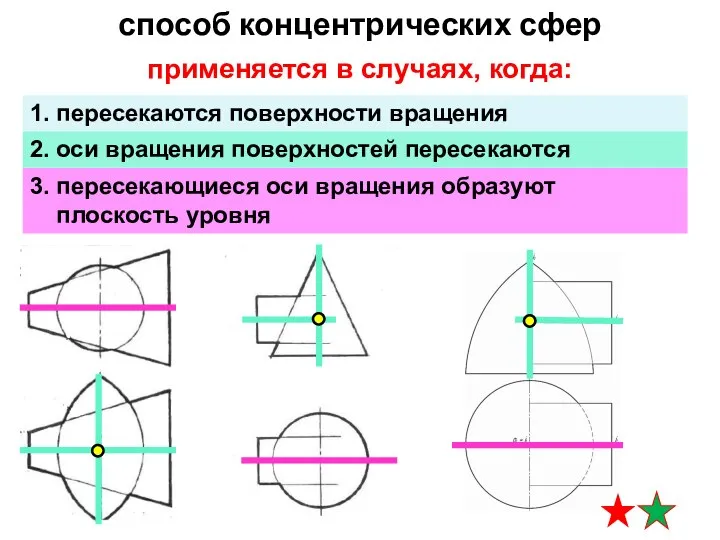
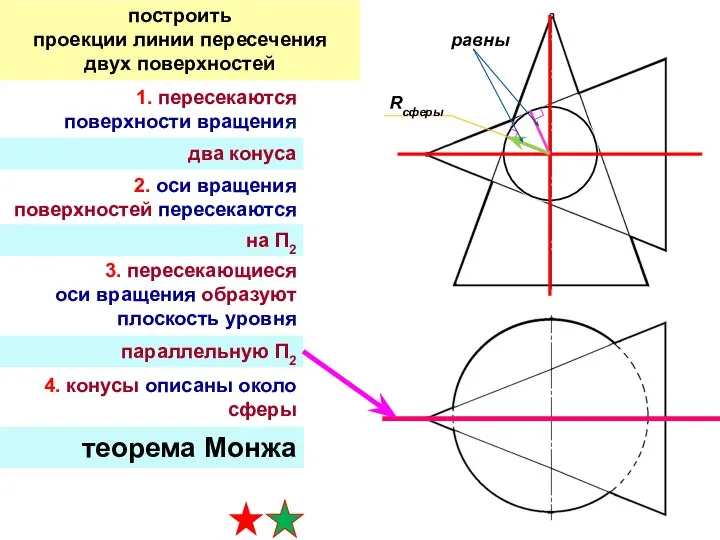
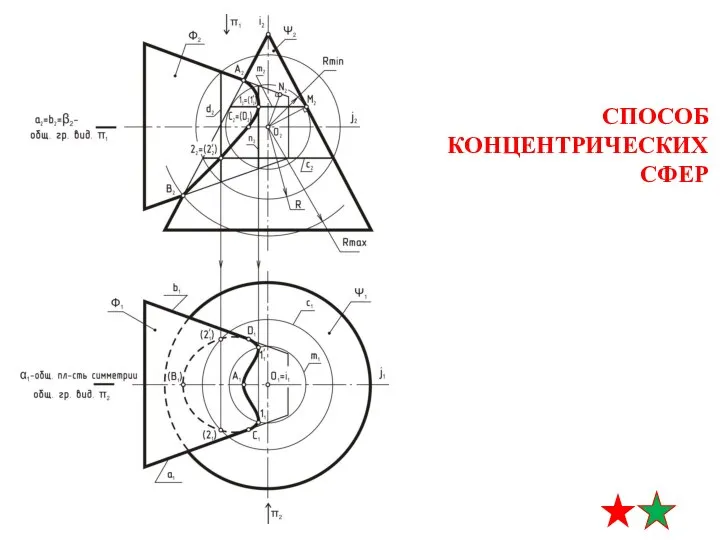
- 11. способ концентрических сфер 1. пересекаются поверхности вращения 2. оси вращения поверхностей пересекаются 3. пересекающиеся оси вращения
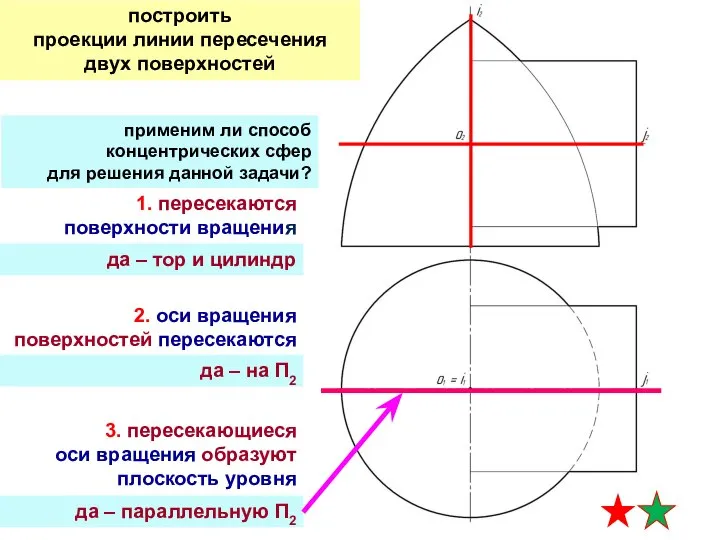
- 12. применим ли способ концентрических сфер для решения данной задачи? 1. пересекаются поверхности вращения 2. оси вращения
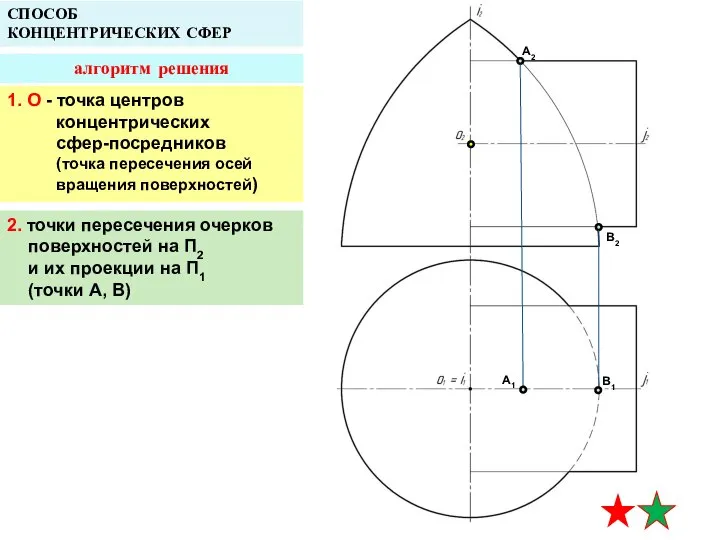
- 13. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 1. О - точка центров концентрических сфер-посредников (точка пересечения осей вращения
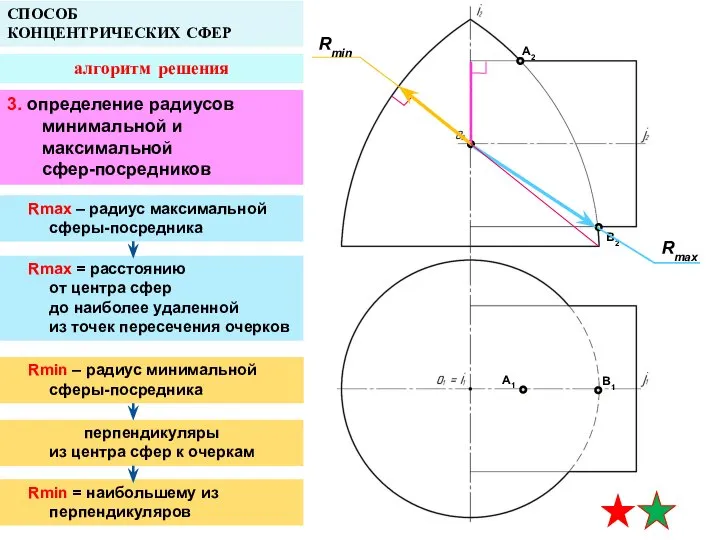
- 14. A2 B2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 3. определение радиусов минимальной и максимальной сфер-посредников
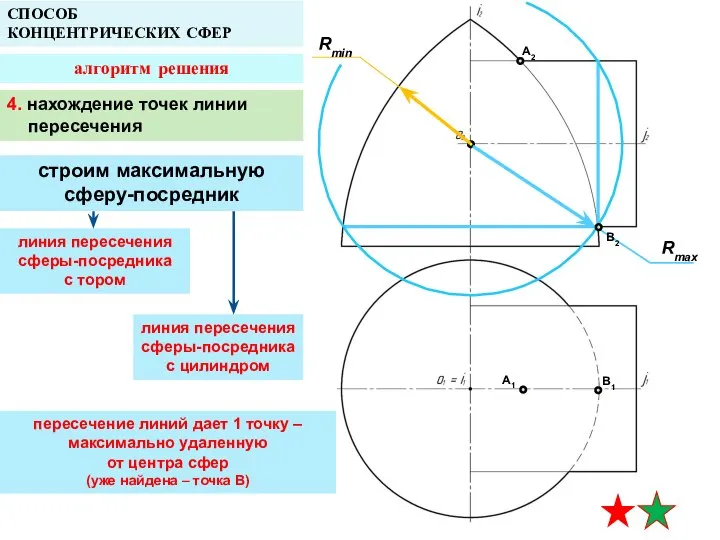
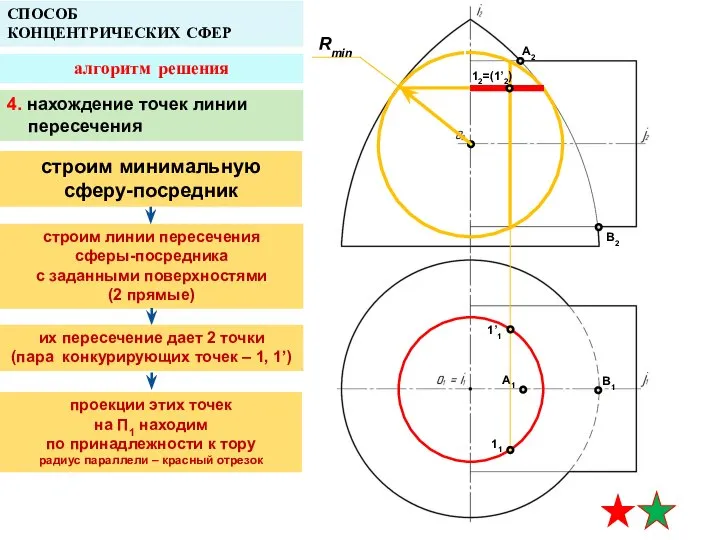
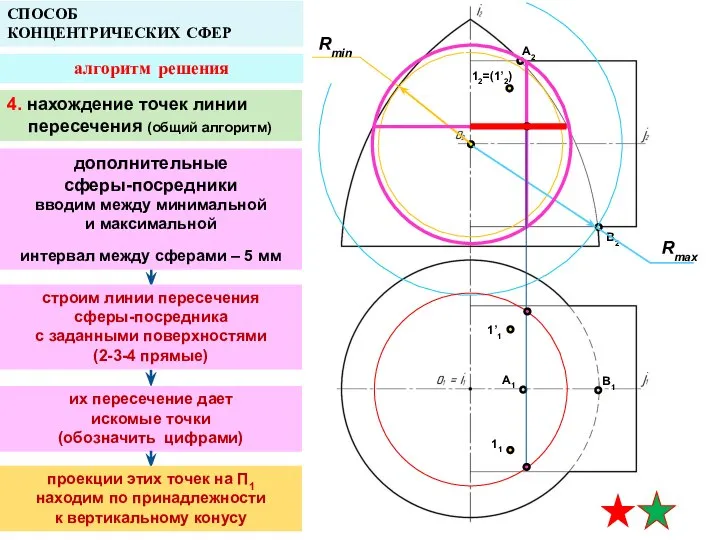
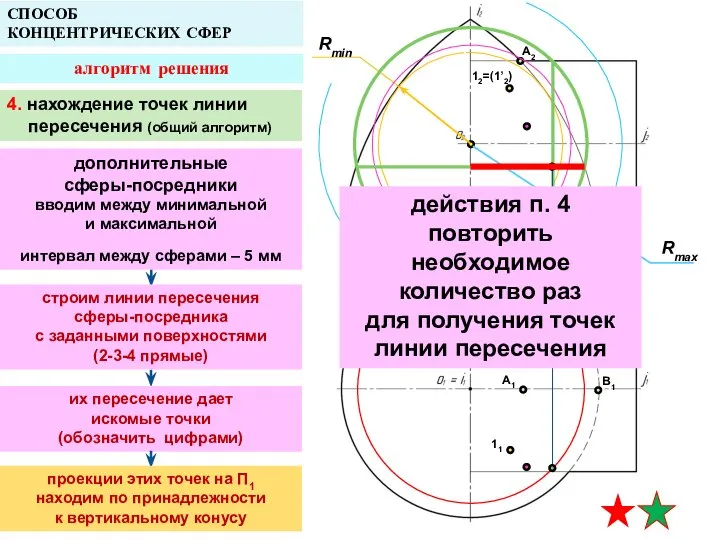
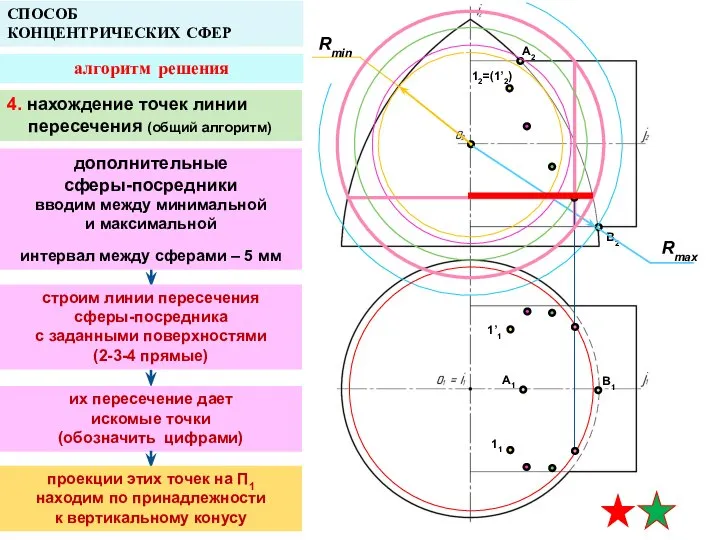
- 15. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmax Rmin 4. нахождение точек линии пересечения строим
- 16. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 4. нахождение точек линии пересечения строим
- 17. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
- 18. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
- 19. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Rmin B2 12=(1’2) 1’1 11 Rmax 4. нахождение
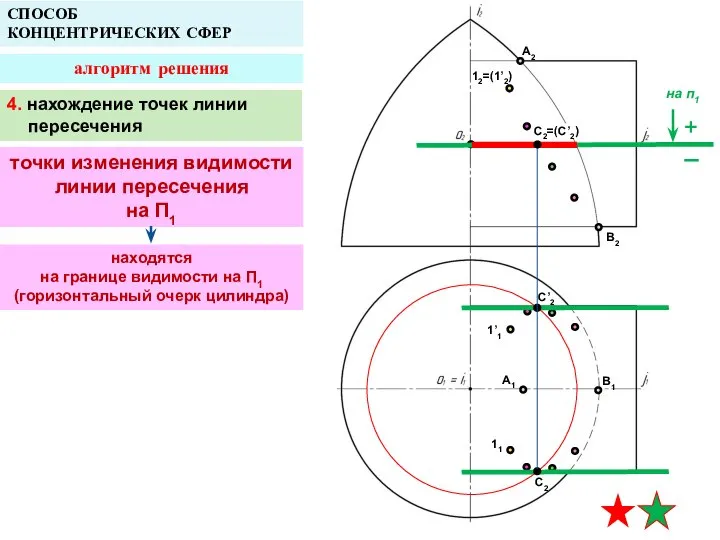
- 20. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 находятся на границе видимости
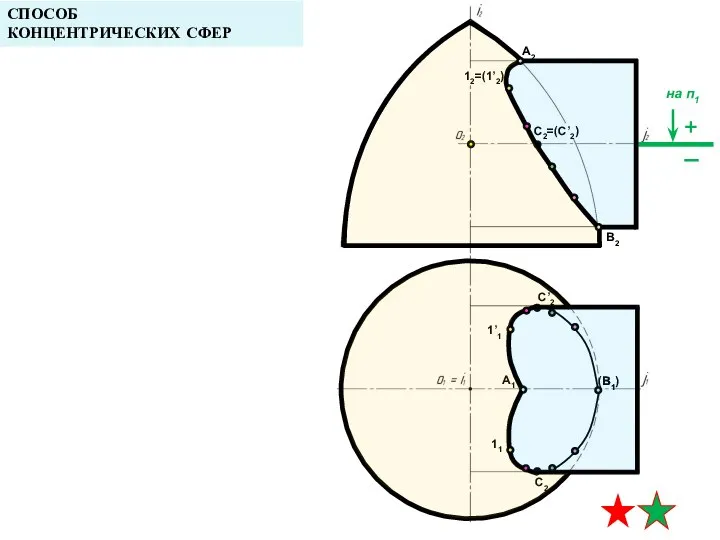
- 21. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 5.
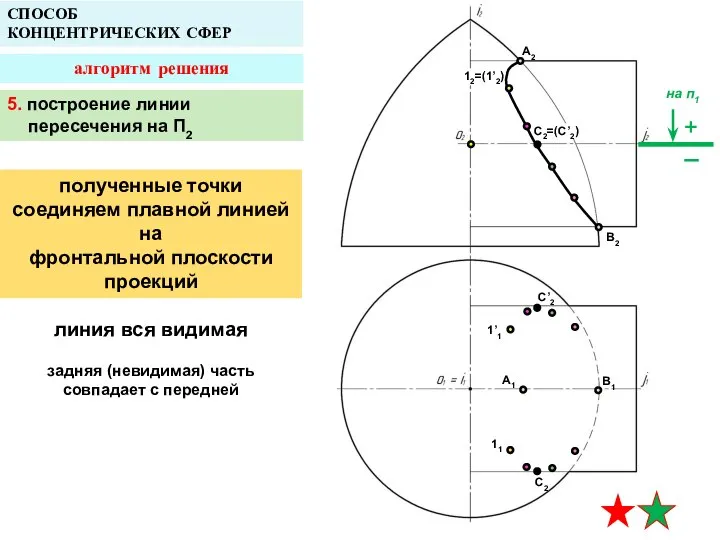
- 22. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 6.
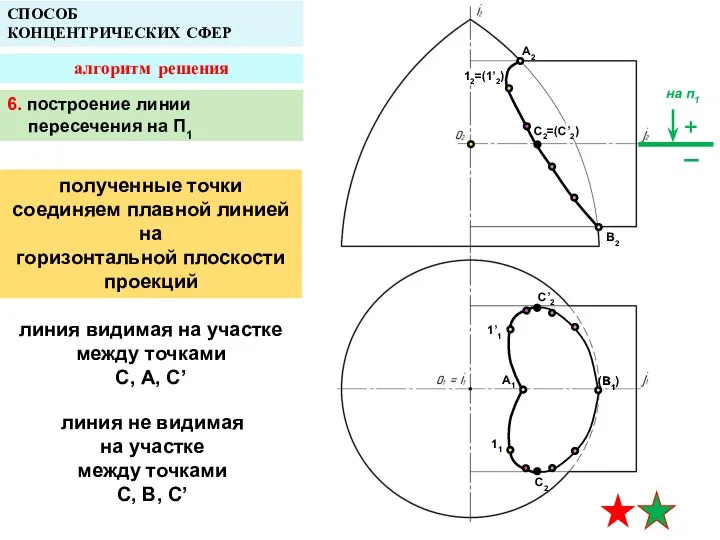
- 23. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР алгоритм решения B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 (B1)
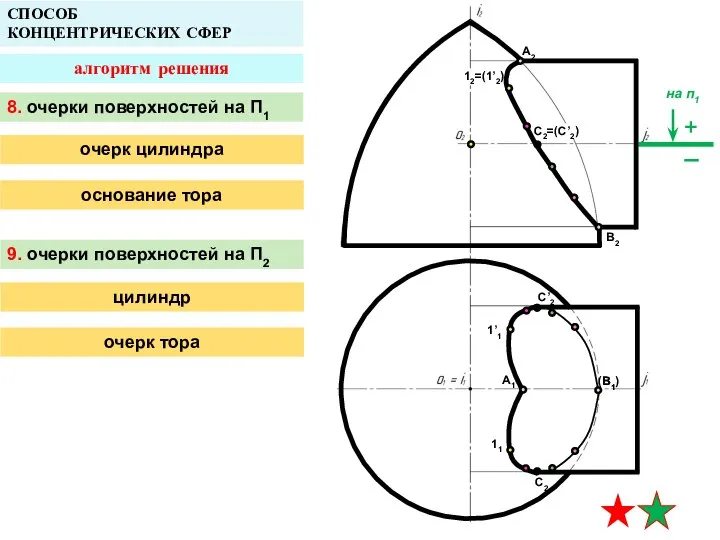
- 24. A2 A1 B1 СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР B2 12=(1’2) 1’1 11 C2=(C’2) C’2 C2 (B1)
- 25. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
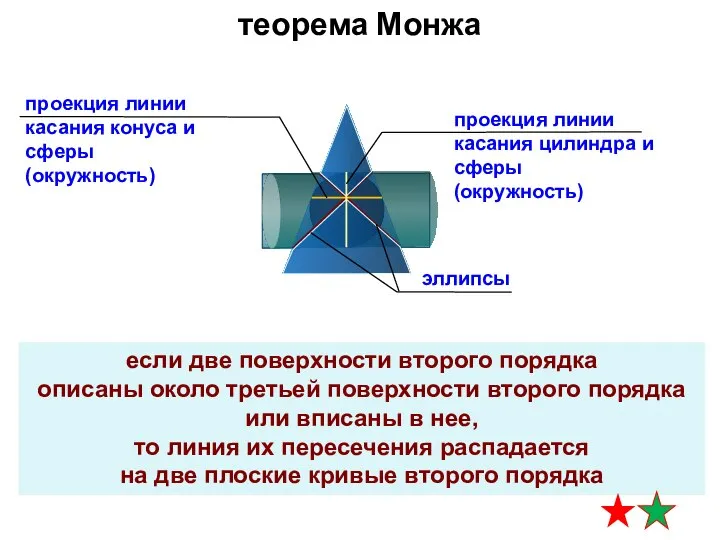
- 26. если две поверхности второго порядка описаны около третьей поверхности второго порядка или вписаны в нее, то
- 27. 1. пересекаются поверхности вращения 2. оси вращения поверхностей пересекаются 3. пересекающиеся оси вращения образуют плоскость уровня
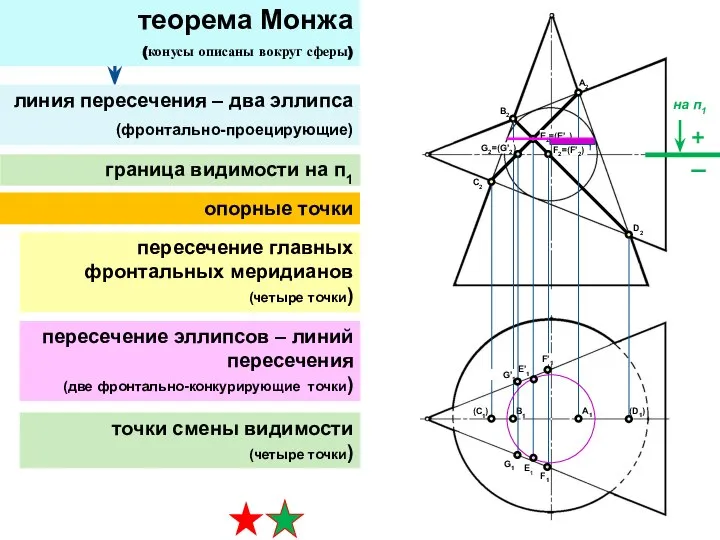
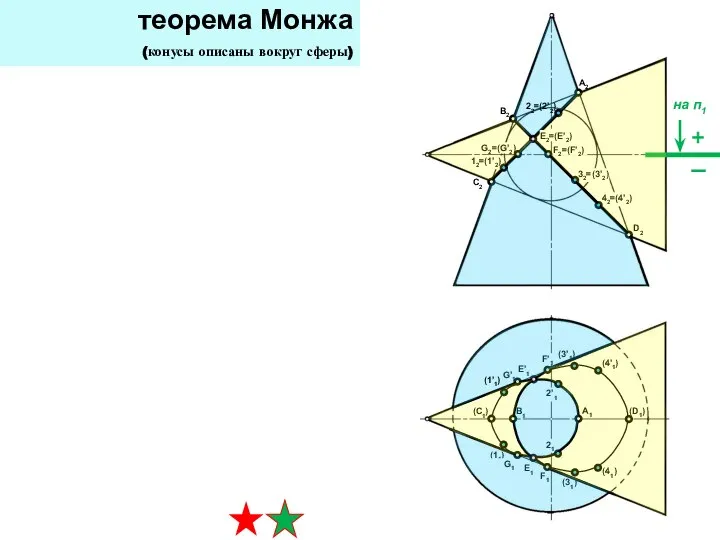
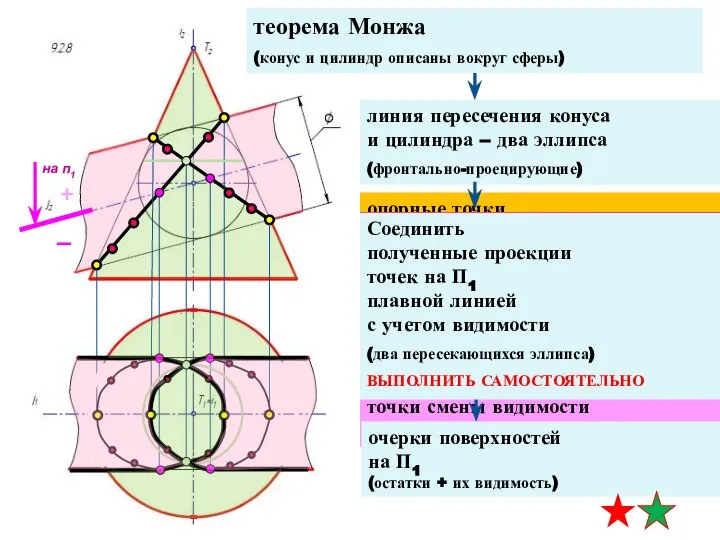
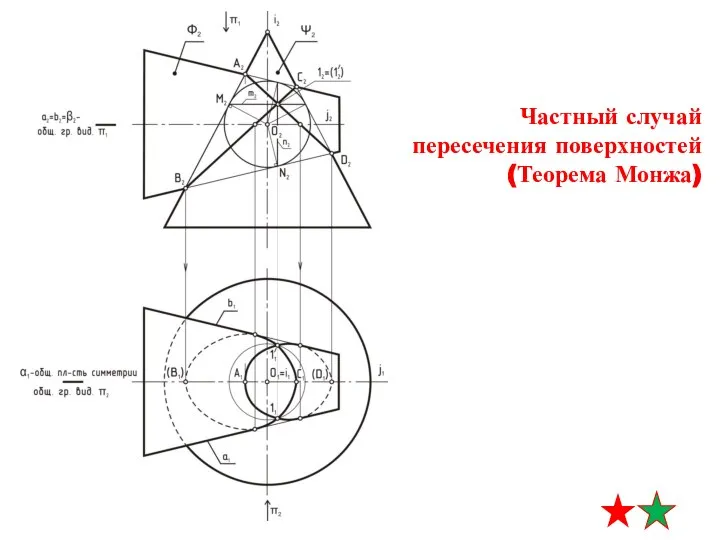
- 28. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) опорные точки пересечение главных
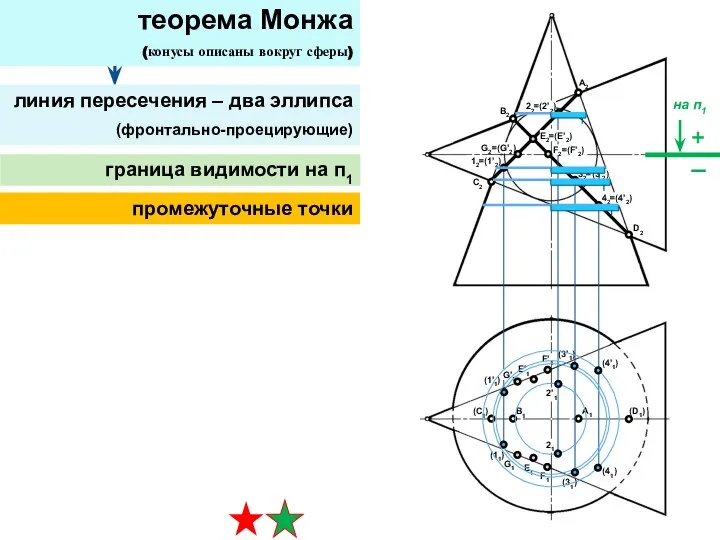
- 29. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) промежуточные точки граница видимости
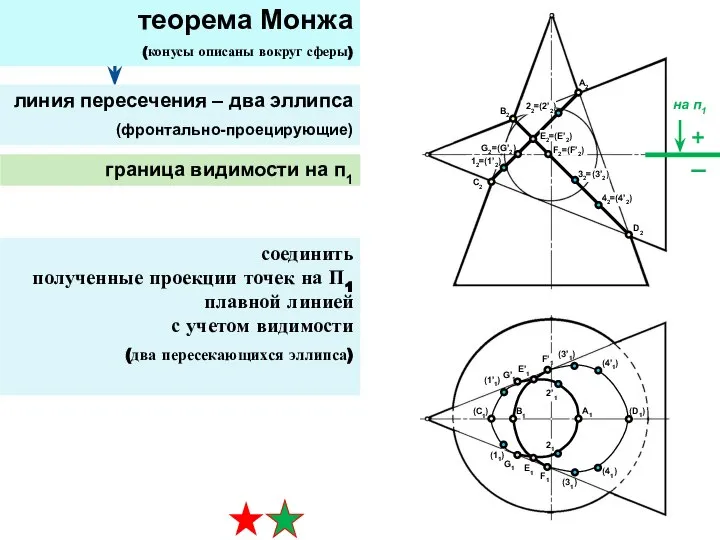
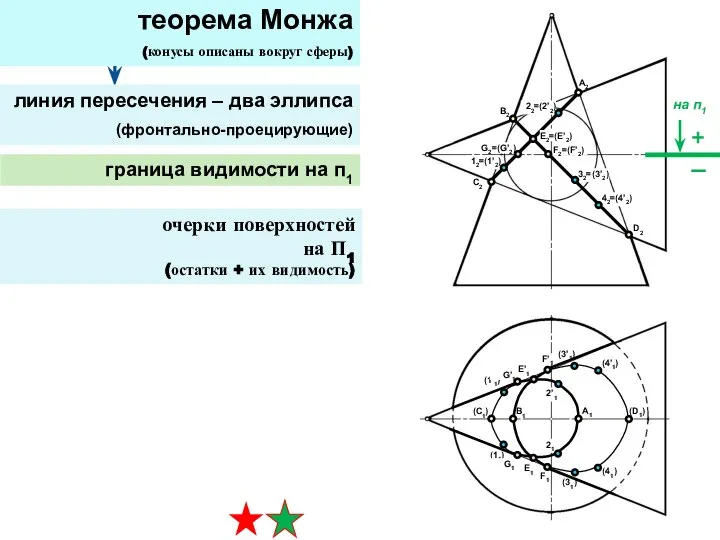
- 30. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) граница видимости на п1
- 31. теорема Монжа (конусы описаны вокруг сферы) линия пересечения – два эллипса (фронтально-проецирующие) граница видимости на п1
- 32. теорема Монжа (конусы описаны вокруг сферы)
- 33. построить на П1 по принадлежности к конусу (САМОСТОЯТЕЛЬНО) пересечение главных фронтальных меридианов (четыре точки) теорема Монжа
- 34. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
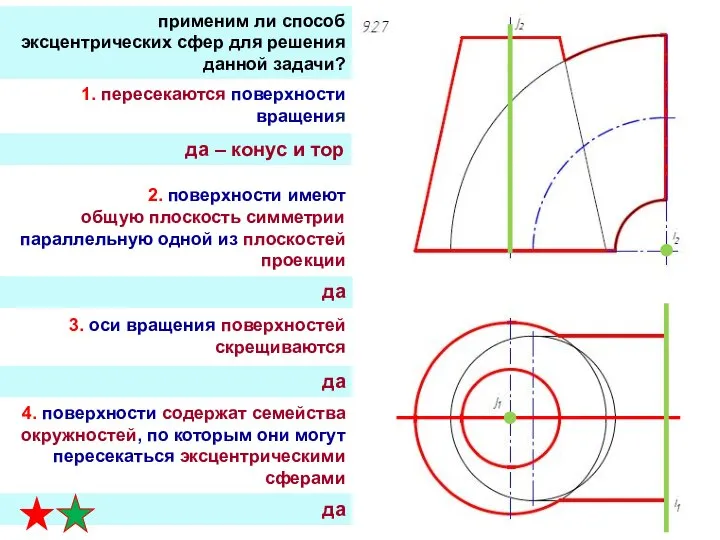
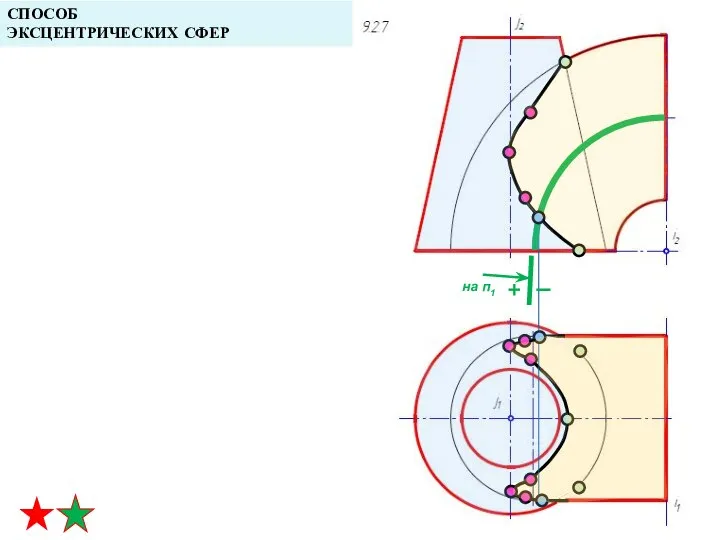
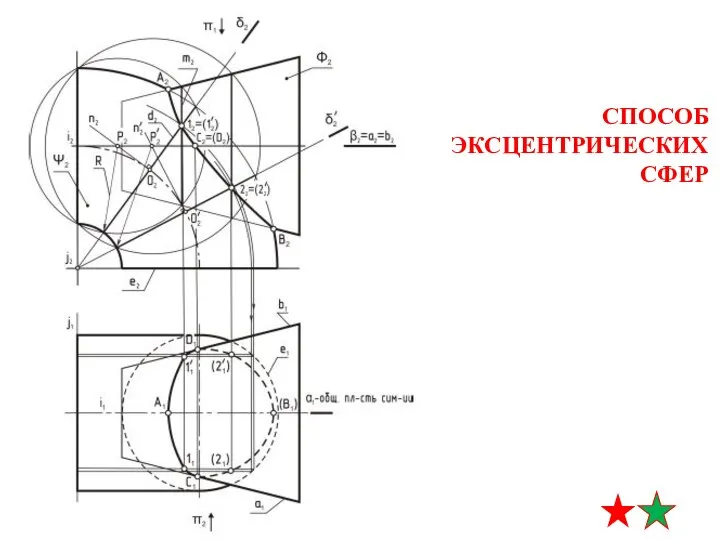
- 35. применим ли способ эксцентрических сфер для решения данной задачи? 1. пересекаются поверхности вращения 3. оси вращения
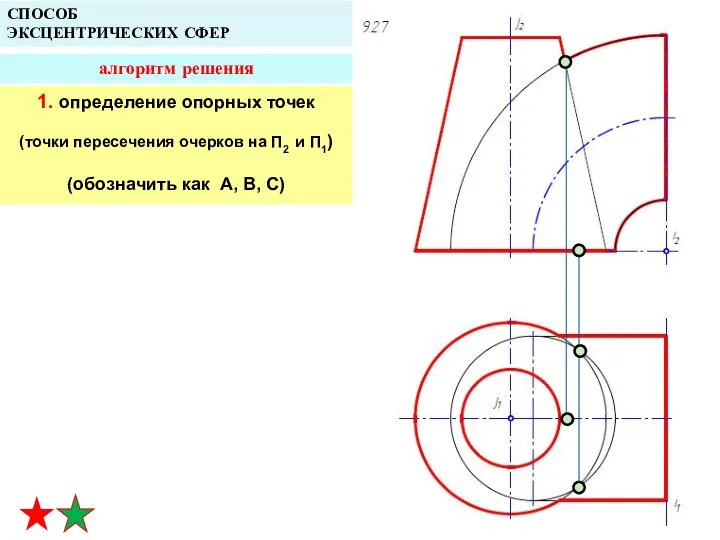
- 36. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 1. определение опорных точек (точки пересечения очерков на П2 и П1)
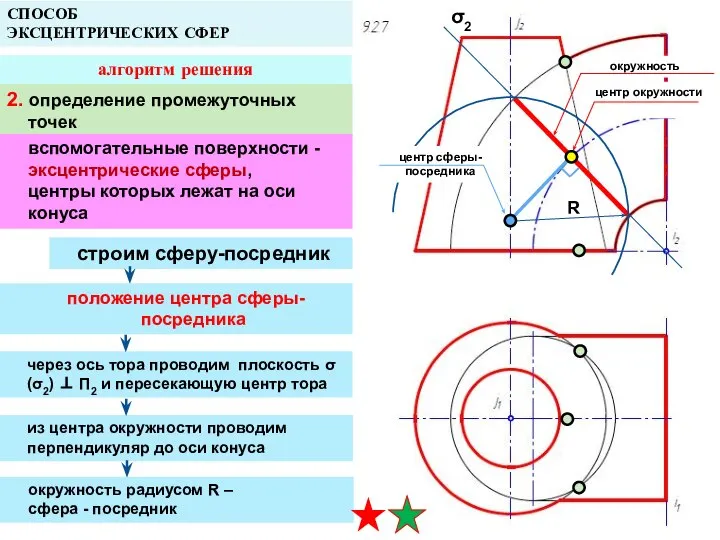
- 37. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 2. определение промежуточных точек вспомогательные поверхности - эксцентрические сферы, центры которых
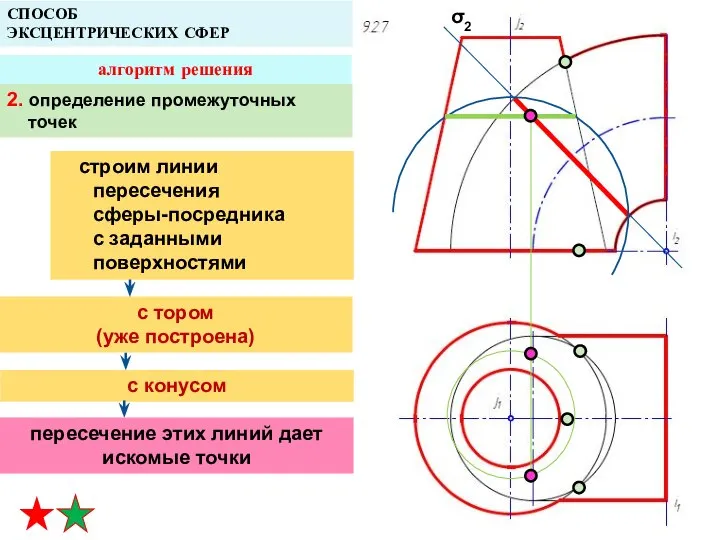
- 38. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения 2. определение промежуточных точек строим линии пересечения сферы-посредника с заданными поверхностями
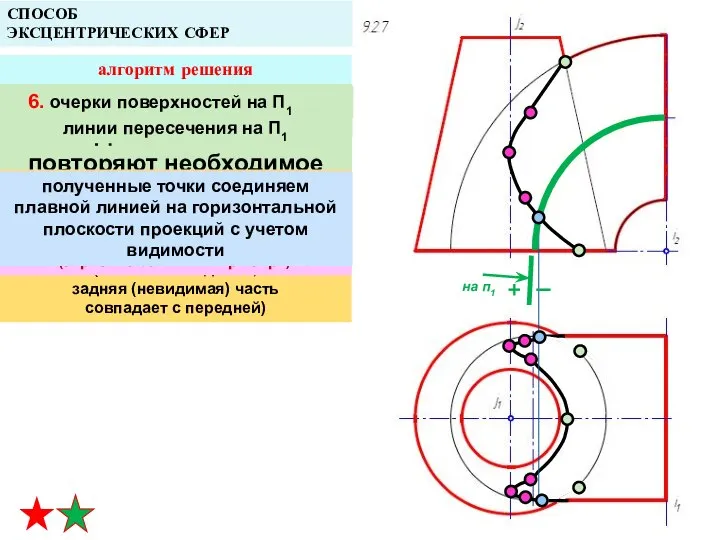
- 39. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР алгоритм решения Действия п. 2 повторяют необходимое количество раз для получения точек линии
- 40. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР на п1
- 41. Содержание лекции методы построения линии пересечения двух поверхностей (Часть 2) способ концентрических сфер частный случай пересечения
- 42. СПОСОБ КОНЦЕНТРИЧЕСКИХ СФЕР
- 43. СПОСОБ ЭКСЦЕНТРИЧЕСКИХ СФЕР
- 44. Частный случай пересечения поверхностей (Теорема Монжа)
- 46. Скачать презентацию


 Нетарифное регулирование ВЭД
Нетарифное регулирование ВЭД Инвестиционная деятельность предприятия
Инвестиционная деятельность предприятия Основные направления деятельности студенческих отрядов
Основные направления деятельности студенческих отрядов -sE dE bile
-sE dE bile НОВЫЕ ПОСТУПЛЕНИЯ ЛИТЕРАТУРЫ
НОВЫЕ ПОСТУПЛЕНИЯ ЛИТЕРАТУРЫ Афиша bts: bring the Soul
Афиша bts: bring the Soul Воды суши
Воды суши Презентация на тему Растительность пойм
Презентация на тему Растительность пойм  ВИХОВНИЙ ЗАХІД“СВЯТО ПОКРОВИ”
ВИХОВНИЙ ЗАХІД“СВЯТО ПОКРОВИ” СПО в России
СПО в России «Работа социально-психологической службыГОУ СОШ № 236 СОУО ДО г. Москвы».Зам. директора по соц. защите: Лисюкова Е.А.Социальный пед
«Работа социально-психологической службыГОУ СОШ № 236 СОУО ДО г. Москвы».Зам. директора по соц. защите: Лисюкова Е.А.Социальный пед ООО Корзина Севастополь
ООО Корзина Севастополь Полярные пустыни и тундры
Полярные пустыни и тундры ИСТОЧНИКОВЕДЕНИЕ И ИСТОРИЯ КНИГИ
ИСТОЧНИКОВЕДЕНИЕ И ИСТОРИЯ КНИГИ О компании БЕЛТАНК
О компании БЕЛТАНК Казимир Малевич
Казимир Малевич Оптимизация химико-технологических процессов
Оптимизация химико-технологических процессов синдром Марфана 11 класс
синдром Марфана 11 класс Новые лекарственные формы и системы доставки лекарственных средств
Новые лекарственные формы и системы доставки лекарственных средств МОУ – СОШ №5 учитель химии Харитонова Марина Вячеславовна I квалификационная категорияСтаж работы 21 год
МОУ – СОШ №5 учитель химии Харитонова Марина Вячеславовна I квалификационная категорияСтаж работы 21 год ОПЕРАЦИЮ ОТРЯД ОСОБОГО НОВОГОДНЕГО НАЗНАЧЕНИЯ «ОСНН-2012»
ОПЕРАЦИЮ ОТРЯД ОСОБОГО НОВОГОДНЕГО НАЗНАЧЕНИЯ «ОСНН-2012» Полупроводниковые лазеры
Полупроводниковые лазеры Основные виды композиции
Основные виды композиции Сибирская хаска
Сибирская хаска Классицизм 17-19 вв
Классицизм 17-19 вв Презентация на тему Как живут растения (1 класс)
Презентация на тему Как живут растения (1 класс) Универсальный Вакуумный Насос
Универсальный Вакуумный Насос Ecological problems
Ecological problems