Перпендикуляр и наклонная

На одном из предыдущих уроков вы познакомились с понятием проекции точки на данную плоскость параллельно данной прямой.
На этом уроке вы продолжите изучение прямых и плоскостей; узнаете, как находится угол между прямой и плоскостью. Вы познакомитесь с понятием ортогональной проекции на плоскость и рассмотрите ее свойства. На уроке будут даны определения расстояния от точки до плоскости и от точки до прямой, угла между прямой и плоскостью. Будет доказана знаменитая теорема о трех перпендикулярах.

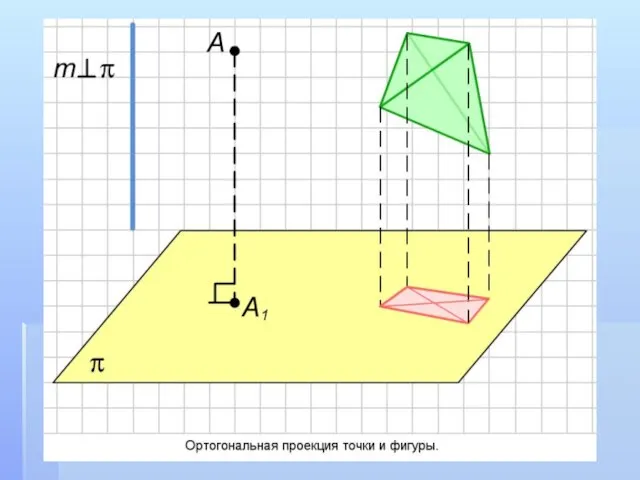
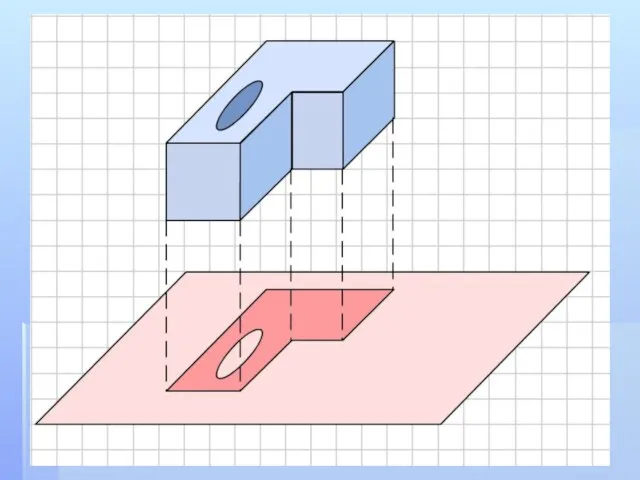
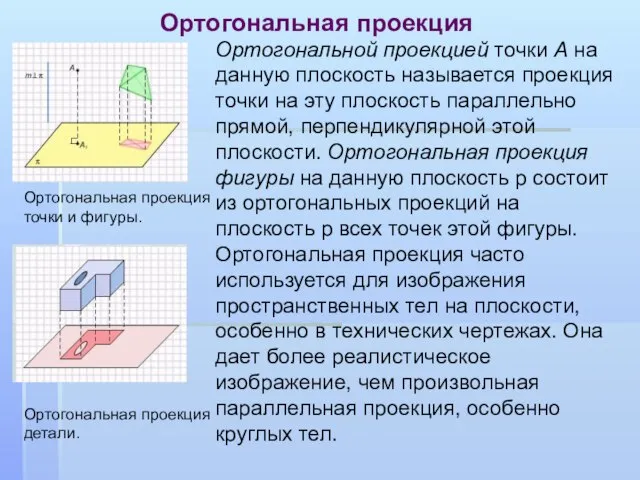
Ортогональной проекцией точки А на данную плоскость называется проекция точки на эту плоскость параллельно прямой, перпендикулярной этой плоскости. Ортогональная проекция фигуры на данную плоскость p состоит из ортогональных проекций на плоскость p всех точек этой фигуры.
Ортогональная проекция часто используется для изображения пространственных тел на плоскости, особенно в технических чертежах. Она дает более реалистическое изображение, чем произвольная параллельная проекция, особенно круглых тел.
Ортогональная проекция
Ортогональная проекция
точки и фигуры.
Ортогональная проекция
детали.

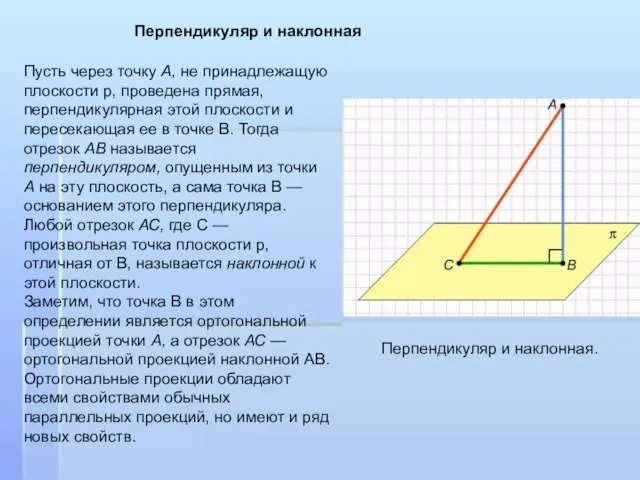
Пусть через точку А, не принадлежащую плоскости p, проведена прямая, перпендикулярная этой плоскости и пересекающая ее в точке В. Тогда отрезок АВ называется перпендикуляром, опущенным из точки А на эту плоскость, а сама точка В — основанием этого перпендикуляра. Любой отрезок АС, где С — произвольная точка плоскости p, отличная от В, называется наклонной к этой плоскости.
Заметим, что точка В в этом определении является ортогональной проекцией точки А, а отрезок АС — ортогональной проекцией наклонной AВ. Ортогональные проекции обладают всеми свойствами обычных параллельных проекций, но имеют и ряд новых свойств.
Перпендикуляр и наклонная
Перпендикуляр и наклонная.

Свойства ортогональной проекции
Пусть из одной точки к плоскости проведены перпендикуляр и несколько наклонных. Тогда справедливы следующие утверждения.
1. Любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость.
2. Равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны.
3. Одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной.

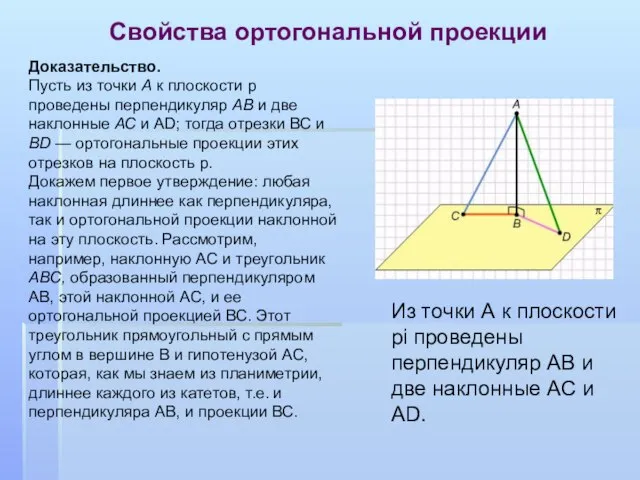
Свойства ортогональной проекции
Доказательство.
Пусть из точки А к плоскости p проведены перпендикуляр АВ и две наклонные АС и AD; тогда отрезки ВС и BD — ортогональные проекции этих отрезков на плоскость p.
Докажем первое утверждение: любая наклонная длиннее как перпендикуляра, так и ортогональной проекции наклонной на эту плоскость. Рассмотрим, например, наклонную AС и треугольник ABC, образованный перпендикуляром AВ, этой наклонной AС, и ее ортогональной проекцией ВС. Этот треугольник прямоугольный с прямым углом в вершине В и гипотенузой AС, которая, как мы знаем из планиметрии, длиннее каждого из катетов, т.е. и перпендикуляра AВ, и проекции ВС.
Из точки А к плоскости pi проведены перпендикуляр АВ и две наклонные AC и AD.

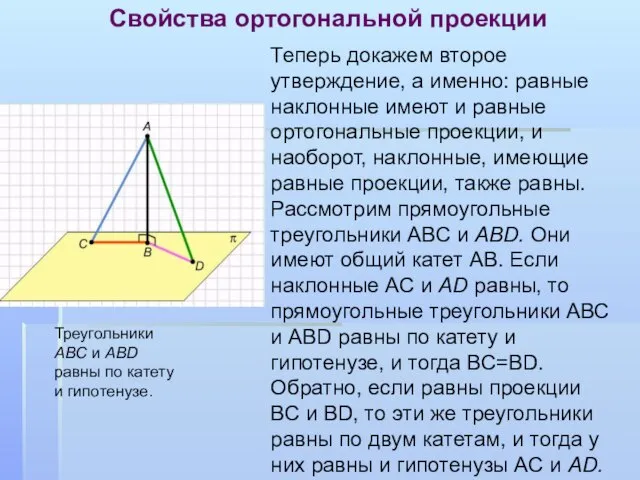
Свойства ортогональной проекции
Теперь докажем второе утверждение, а именно: равные наклонные имеют и равные ортогональные проекции, и наоборот, наклонные, имеющие равные проекции, также равны.
Рассмотрим прямоугольные треугольники AВС и ABD. Они имеют общий катет AВ. Если наклонные AС и AD равны, то прямоугольные треугольники AВС и AВD равны по катету и гипотенузе, и тогда BC=BD. Обратно, если равны проекции ВС и BD, то эти же треугольники равны по двум катетам, и тогда у них равны и гипотенузы AС и AD.
Треугольники ABC и ABD равны по катету и гипотенузе.

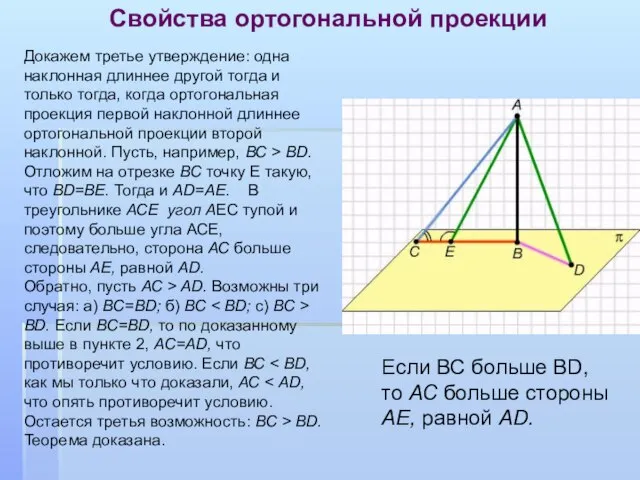
Свойства ортогональной проекции
Докажем третье утверждение: одна наклонная длиннее другой тогда и только тогда, когда ортогональная проекция первой наклонной длиннее ортогональной проекции второй наклонной. Пусть, например, ВС > BD. Отложим на отрезке ВС точку Е такую, что BD=BE. Тогда и AD=AE. В треугольнике АСЕ угол AEC тупой и поэтому больше угла ACE, следовательно, сторона АС больше стороны АЕ, равной AD.
Обратно, пусть АС > AD. Возможны три случая: a) BC=BD; б) ВС < BD; с) ВС > BD. Если BC=BD, то по доказанному выше в пункте 2, AC=AD, что противоречит условию. Если ВС < BD, как мы только что доказали, АС < AD, что опять противоречит условию. Остается третья возможность: ВС > BD. Теорема доказана.
Если ВС больше BD, то АС больше стороны АЕ, равной AD.

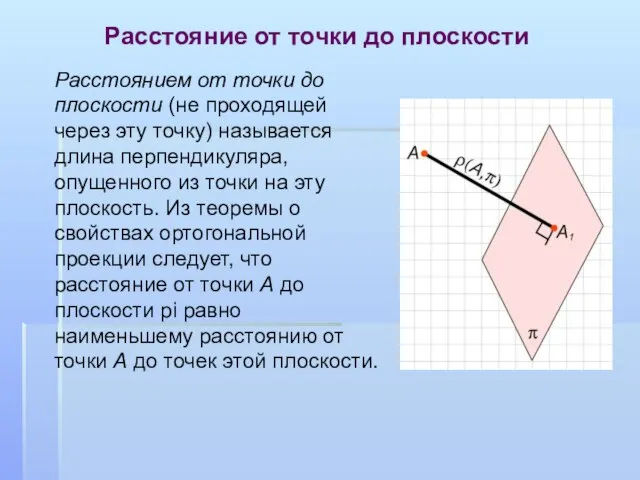
Расстояние от точки до плоскости
Расстоянием от точки до плоскости (не проходящей через эту точку) называется длина перпендикуляра, опущенного из точки на эту плоскость. Из теоремы о свойствах ортогональной проекции следует, что расстояние от точки А до плоскости pi равно наименьшему расстоянию от точки А до точек этой плоскости.

Свойство расстояний
от разных точек до плоскости
Замечание 1 (свойство расстоянии от разных точек до плоскости). Пусть две точки А и В не принадлежат плоскости pi, а прямая АВ пересекает плоскость pi в точке С. Тогда расстояния от точек А и В до плоскости pi относятся как отрезки АС и ВС:

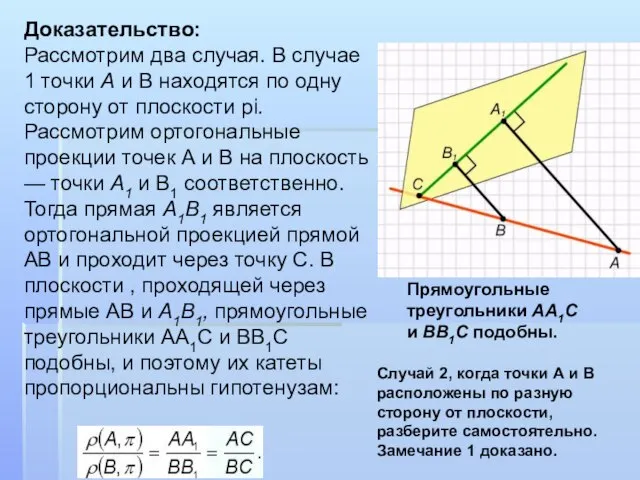
Доказательство:
Рассмотрим два случая. В случае 1 точки А и В находятся по одну сторону от плоскости pi. Рассмотрим ортогональные проекции точек А и В на плоскость — точки А1 и B1 соответственно. Тогда прямая A1B1 является ортогональной проекцией прямой AВ и проходит через точку С. В плоскости , проходящей через прямые AВ и А1В1, прямоугольные треугольники AA1С и BB1C подобны, и поэтому их катеты пропорциональны гипотенузам:
Прямоугольные треугольники AA1C и ВВ1С подобны.
Случай 2, когда точки А и В расположены по разную сторону от плоскости, разберите самостоятельно. Замечание 1 доказано.

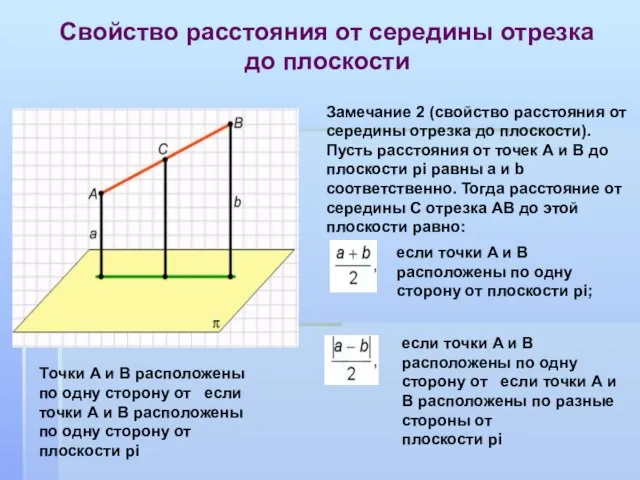
Замечание 2 (свойство расстояния от середины отрезка до плоскости).
Пусть расстояния от точек А и B до плоскости pi равны а и b соответственно. Тогда расстояние от середины С отрезка АВ до этой плоскости равно:
Свойство расстояния от середины отрезка
до плоскости
Tочки A и B расположены по одну сторону от если точки А и B расположены по одну сторону от плоскости pi
если точки A и B расположены по одну сторону от плоскости pi;
если точки A и B расположены по одну сторону от если точки А и B расположены по разные стороны от
плоскости pi

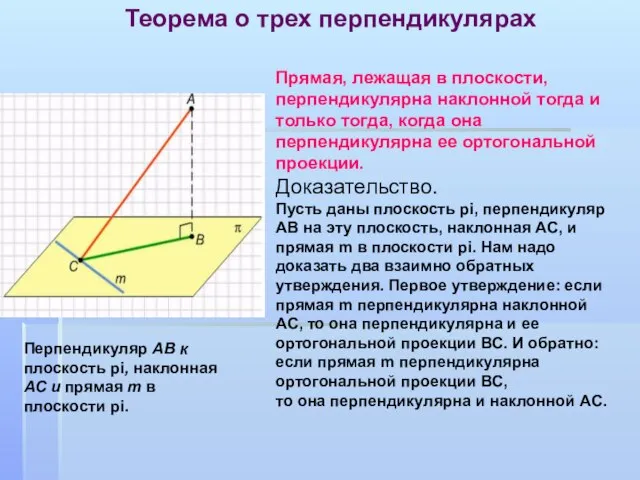
Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна ее ортогональной проекции.
Доказательство.
Пусть даны плоскость pi, перпендикуляр АВ на эту плоскость, наклонная АС, и прямая m в плоскости pi. Нам надо доказать два взаимно обратных утверждения. Первое утверждение: если прямая m перпендикулярна наклонной АС, то она перпендикулярна и ее ортогональной проекции ВС. И обратно: если прямая m перпендикулярна ортогональной проекции ВС,
то она перпендикулярна и наклонной АС.
Перпендикуляр АВ к плоскость pi, наклонная АС и прямая т в плоскости pi.
Теорема о трех перпендикулярах

Прямая m перпендикулярна плоскости АВС.

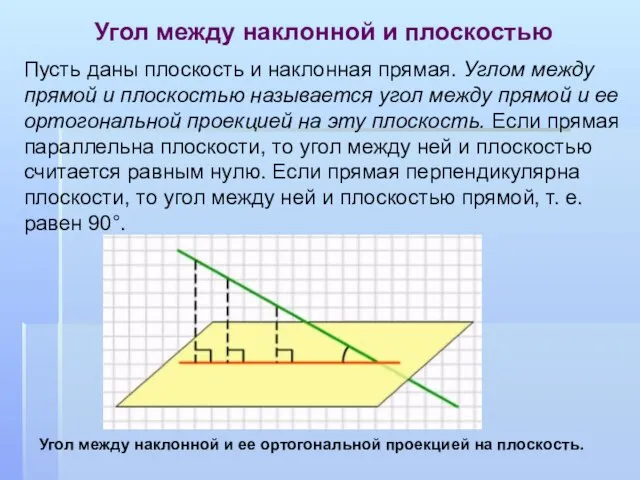
Пусть даны плоскость и наклонная прямая. Углом между прямой и плоскостью называется угол между прямой и ее ортогональной проекцией на эту плоскость. Если прямая параллельна плоскости, то угол между ней и плоскостью считается равным нулю. Если прямая перпендикулярна плоскости, то угол между ней и плоскостью прямой, т. е. равен 90°.
Угол между наклонной и плоскостью
Угол между наклонной и ее ортогональной проекцией на плоскость.

Перпендикуляр, наклонная и ее
ортогональная проекция образуют
прямоугольный треугольник.