Слайд 2ЗАДАНИЕ
1. Выполнить чертёж
2. Внимательно изучить определения
3. Запиать все определения буквами, например:ВС -

перпендикуляр, АВ -наклонная, А - основание перпендкуляра ...( пять определений)
4. Рассмотреть решение задачи №1 внимательно и решить подобную задачу №2
Слайд 3Пусть дана плоскость α и не лежащая на ней точка А
α
А
В
С
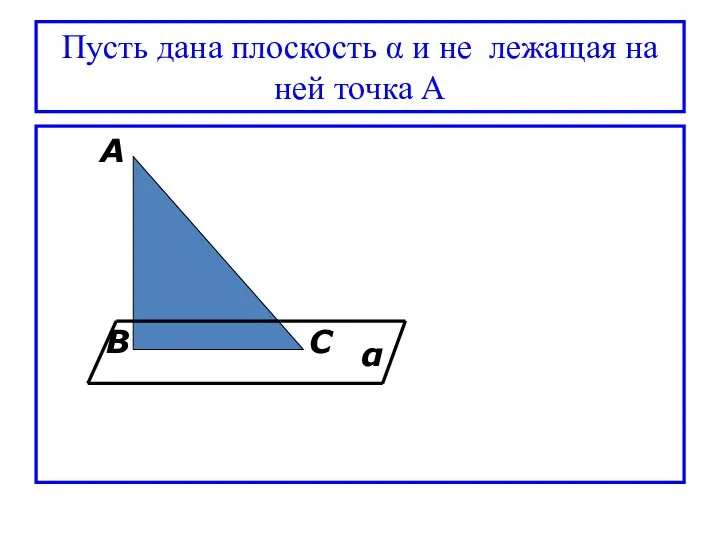
Слайд 4Перпендикуляром, опущенным из данной точки на данную плоскость называется отрезок соединяющий данную

точку с точкой на плоскости и лежащий на прямой, перпендикулярной плоскости
Слайд 5Основанием перпендикуляра
называется точка пересечения перпендикуляра с плоскостью

Слайд 6Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий

данную точку с точкой на плоскости , не являющийся перпендикуляром к плоскости
Слайд 7Основанием наклонной
называется точка пересечения наклонной с плоскостью
Слайд 8Проекцией наклонной называется отрезок, соединяющий основание перпендикуляра и наклонной, проведенных из одной

точки
Слайд 9Задача №1
Верхние концы двух вертикально стоящих столбов, удаленных на расстояние 3,4 м,

соединены перекладиной. Высота одного столба 5,8 м, а другого 3,9м.
Найдите длину перекладины
Слайд 10 Дано:
АВ = 5,8 м
СД = 3,9 м
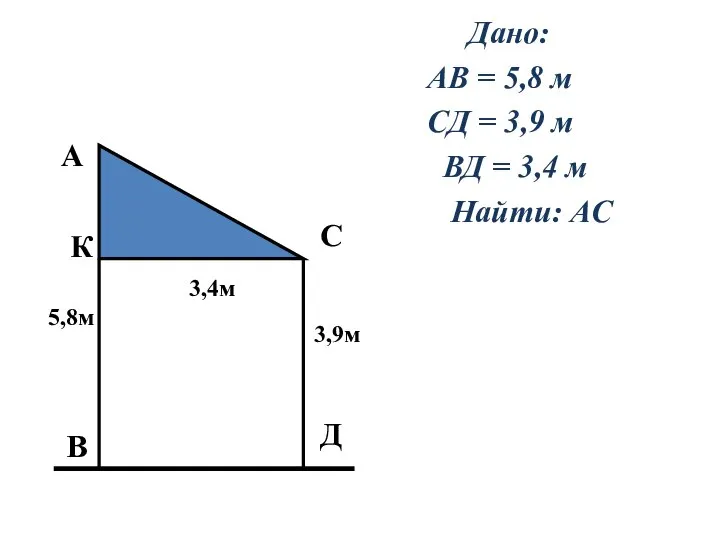
ВД = 3,4 м
Найти: АС
С
В
Д
К
3,4м
5,8м
3,9м
А
Слайд 11Образец решения задачи№1
∆ АКС: По теореме Пифагора
АС2 = АК 2+ КС2
Находим

АК = АВ - СД
АК = 5,8 - 3,9 = 1,9(м)
КС = ВД = 3,4(м) (видно из рисунка, по построению)
АС2 = 1,9 2+ 3,42
АС2 = 3,61+ 11, 56
АС2 = 15,17
АС = √15,17 ≈ 3,9 (м) Ответ: АС ≈ 3,9 м
Слайд 12РЕШИТЬ САМОСТОЯТЕЛЬНО. Задача №2
Верхние концы двух вертикально стоящих столбов, удаленных на расстояние

3м, соединены перекладиной. Высота одного столба 18 м, а другого 14м.
Найдите длину перекладины
Слайд 13Задача №3
Телефонная проволока длиной 15м. протянута от телефонного столба, где она прикреплена

на высоте 8 м.
от поверхности земли, к дому
на высоте 20м. Найдите расстояние между домом и столбом
Слайд 14Задача №4
Из точки к плоскости проведены две наклонные, равные 17 и 10

см. Разность проекций наклонных равна 9 см. Найти проекции наклонных
Слайд 15 Дано:
АВ = 17 см
ВС = 10 см
АД -
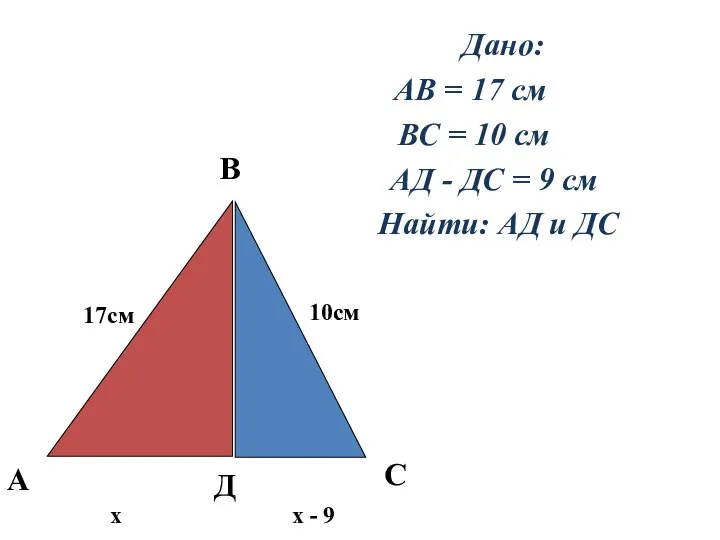
ДС = 9 см
Найти: АД и ДС
А
В
С
Д
17см
10см
х
х - 9
Слайд 16Образец решения задачи № 4
Пусть АД = х, тогда ДС = х
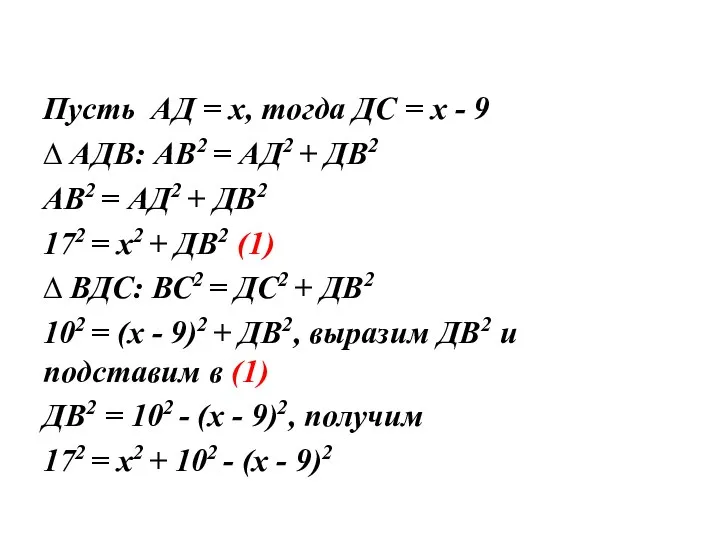
- 9
∆ АДВ: АВ2 = АД2 + ДВ2
АВ2 = АД2 + ДВ2
172 = х2 + ДВ2 (1)
∆ ВДС: ВС2 = ДС2 + ДВ2
102 = (х - 9)2 + ДВ2, выразим ДВ2 и подставим в (1)
ДВ2 = 102 - (х - 9)2, получим
172 = х2 + 102 - (х - 9)2
Слайд 17172 = х2 + 102 - (х - 9)2
289 = х2 +
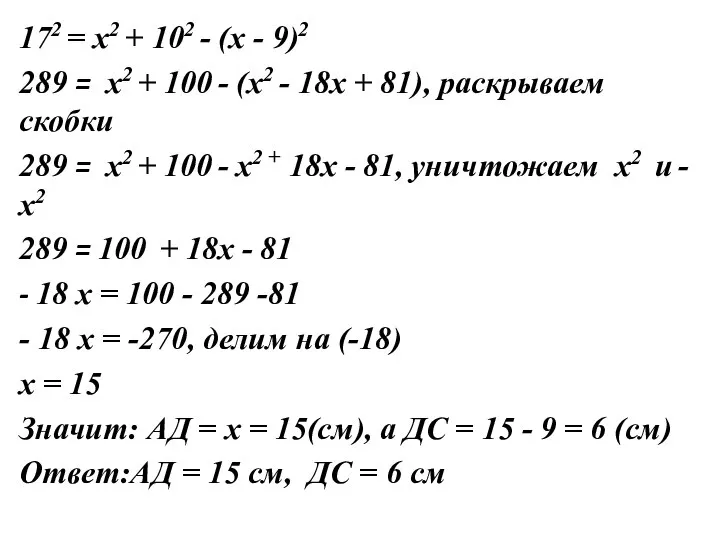
100 - (х2 - 18х + 81), раскрываем скобки
289 = х2 + 100 - х2 + 18х - 81, уничтожаем х2 и - х2
289 = 100 + 18х - 81
- 18 х = 100 - 289 -81
- 18 х = -270, делим на (-18)
х = 15
Значит: АД = х = 15(см), а ДС = 15 - 9 = 6 (см)
Ответ:АД = 15 см, ДС = 6 см














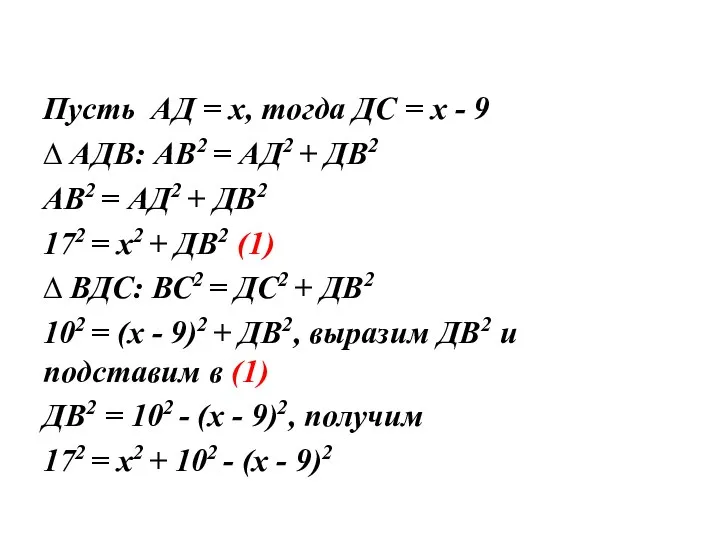
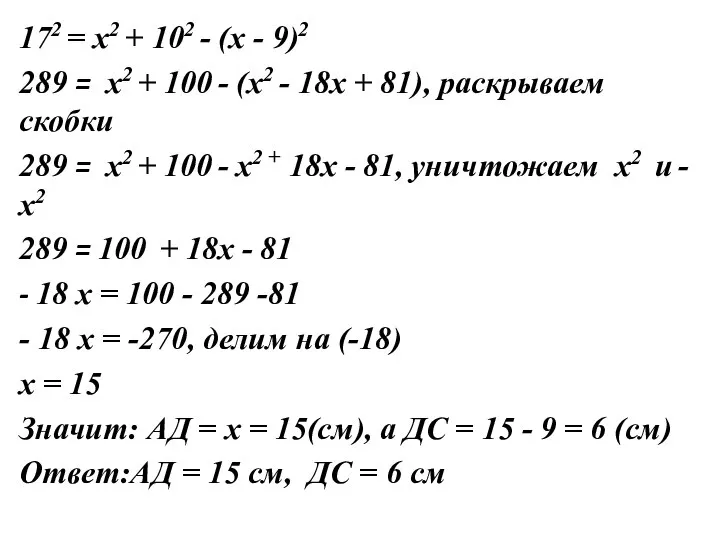
 Бессмертная комедия А. С. Грибоедова «Горе от ума»
Бессмертная комедия А. С. Грибоедова «Горе от ума» Урок коллективного посещения в 5 классе
Урок коллективного посещения в 5 классе ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы.
ПЕДАГОГИЧЕСКИЙ СОВЕТОДАРЁННЫЕ ДЕТИ: реалии, проблемы, перспективы. Ранения. Первая медицинская помощь
Ранения. Первая медицинская помощь Совершенствование сервисно-транспортной инфраструктуры придомовых территорий
Совершенствование сервисно-транспортной инфраструктуры придомовых территорий СТЕКЛЯННЫЕ ТОВАРЫ
СТЕКЛЯННЫЕ ТОВАРЫ Применение электролиза. Основная химическая промышленность
Применение электролиза. Основная химическая промышленность Маршрут прогулки по городу Борисоглебск
Маршрут прогулки по городу Борисоглебск Региональный студенческий хакатон ООО АИС город
Региональный студенческий хакатон ООО АИС город Берегите зрение
Берегите зрение Конкурентные преимущества и перспективы развития казахстанского фондового рынка
Конкурентные преимущества и перспективы развития казахстанского фондового рынка Древние восточные церкви. Православие за рубежом в xх – xxi вв
Древние восточные церкви. Православие за рубежом в xх – xxi вв Pro-психологов: психологическая служба образовательной организации
Pro-психологов: психологическая служба образовательной организации ST Main Page
ST Main Page Лекарственная аллергия
Лекарственная аллергия Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация Развитие координационных способностей у юных борцов вольного стиля
Развитие координационных способностей у юных борцов вольного стиля Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони
Диплом партнёра центра спортивного комплексного обучения по хоккею г. Сморгони МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ
МЕТОДИКА ПРОВЕДЕНИЯ КОРРЕКЦИОННЫХ ЗАНЯТИЙ Политический конфликт
Политический конфликт Чемпионат и первенство города Ярославля по зимнему триатлону
Чемпионат и первенство города Ярославля по зимнему триатлону AI автомобиля в изменчивом мире на примере Ex Machina
AI автомобиля в изменчивом мире на примере Ex Machina Восприятие речи
Восприятие речи Конаково
Конаково Сударыня - Масленица
Сударыня - Масленица Візуальний контакт під час ділової комунікації
Візуальний контакт під час ділової комунікації Технологии проведения избирательной кампании
Технологии проведения избирательной кампании Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»
Общественная организацияг.Балаково Саратовской области«Попечительский совет средней школы №11»