Перпендикулярность

План урока
Немного теории
Полезные упражнения
Составление плана решения задач
Решение задач по готовым чертежам
Тест «Перпендикулярность»
Итог урока
Домашнее задание

Немного теории
Дайте понятие угла между двумя плоскостями.
Сформулируйте определение перпендикулярности двух плоскостей.
Сформулируйте признак перпендикулярности двух плоскостей.
Какая фигура называется двугранным углом? Линейным углом двугранного угла?
Каково взаимное расположение граней двугранного угла и плоскости двугранного угла?
Какой угол образует ребро двугранного угла с любой прямой, лежащей в плоскости его линейного угла?
Можно ли утверждать, что две плоскости перпендикулярные третьей параллельны?
Верно- ли , что прямая и плоскость перпендикулярные другой плоскости, параллельны между собой?
Где лежит высота тупоугольного треугольника, проведенная из вершины острого угла?
В какую трапецию можно вписать окружность?
Свойство касательной и радиуса, проведенного в точку касания.
Свойство высоты прямоугольного треугольника, проведенной к гипотенузе.

Полезные упражнения

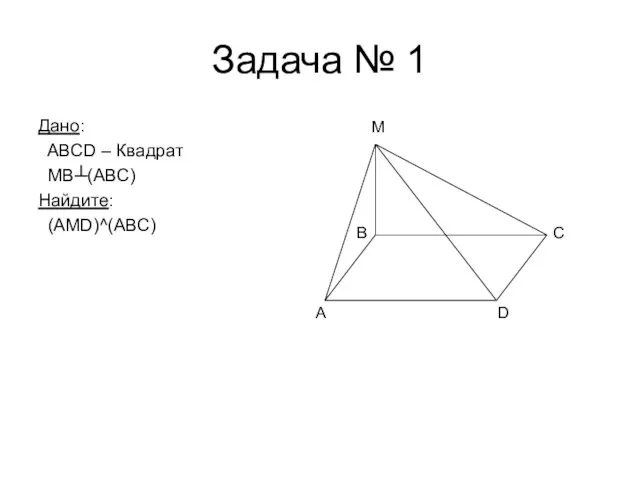
Задача № 1
Дано:
ABCD – Квадрат
MB┴(ABC)
Найдите:
(AMD)^(ABC)
A
D
C
M
B

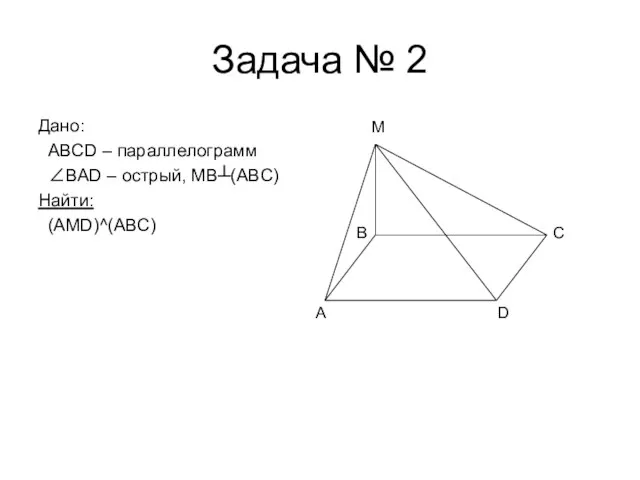
Задача № 2
Дано:
ABCD – параллелограмм
∠BAD – острый, MB┴(ABC)
Найти:
(AMD)^(ABC)
A
D
C
M
B

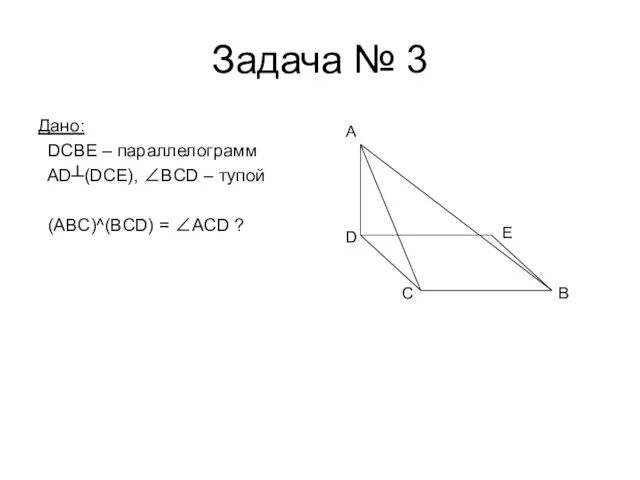
Задача № 3
Дано:
DCBE – параллелограмм
AD┴(DCE), ∠BCD – тупой
(ABC)^(BCD) = ∠ACD ?
C
A
D
E
B

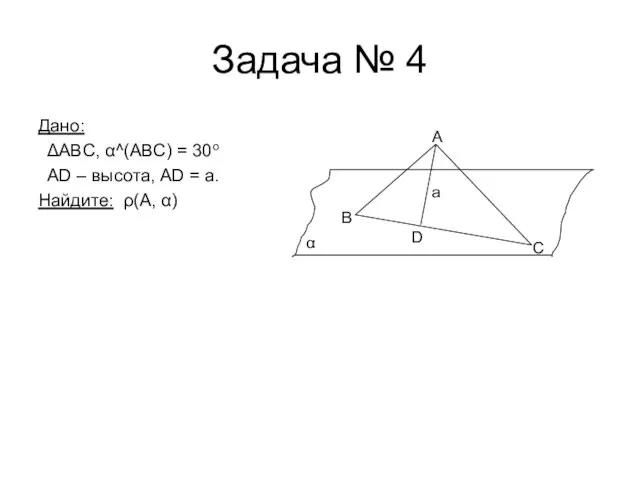
Задача № 4
Дано:
ΔABC, α^(ABC) = 30o
AD – высота, AD = a.
Найдите: ρ(А, α)
А
B
D
C
a
α

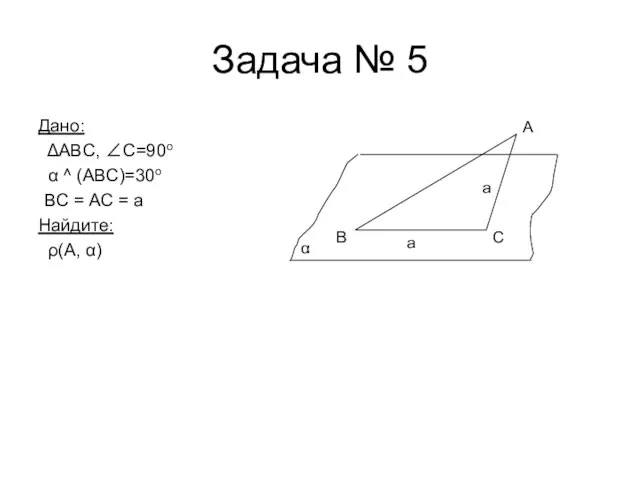
Задача № 5
Дано:
ΔABC, ∠C=90o
α ^ (ABC)=30o
BC = AC = a
Найдите:
ρ(А, α)
B
C
A
a
a
α

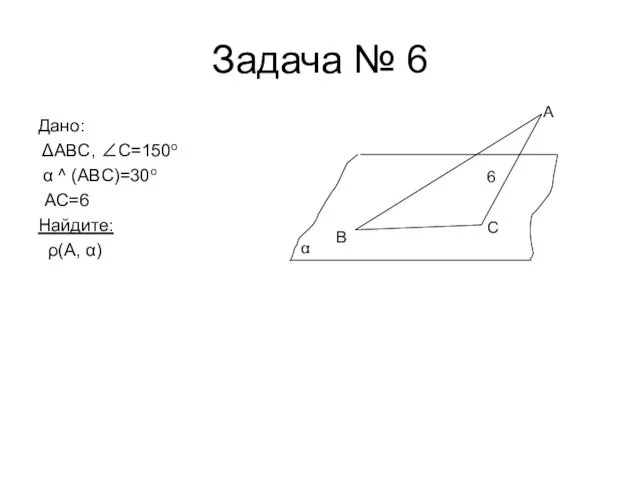
Задача № 6
Дано:
ΔABC, ∠C=150o
α ^ (ABC)=30o
АС=6
Найдите:
ρ(А, α)
B
C
A
6
α

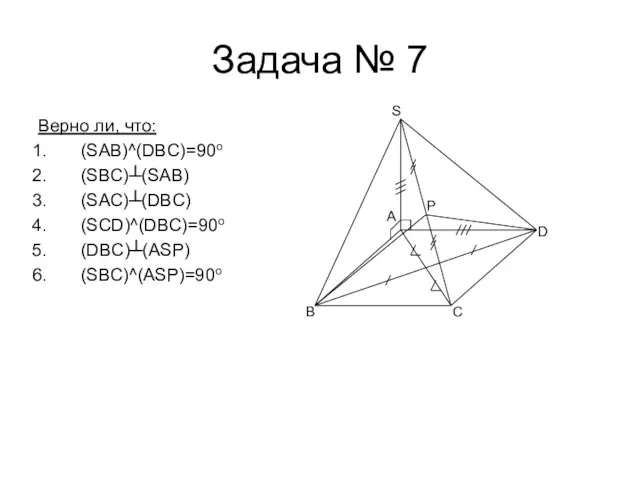
Задача № 7
Верно ли, что:
(SAB)^(DBC)=90o
(SBC)┴(SAB)
(SAC)┴(DBC)
(SCD)^(DBC)=90o
(DBC)┴(ASP)
(SBC)^(ASP)=90o
B
C
D
S
A
P

Составление плана решения задач

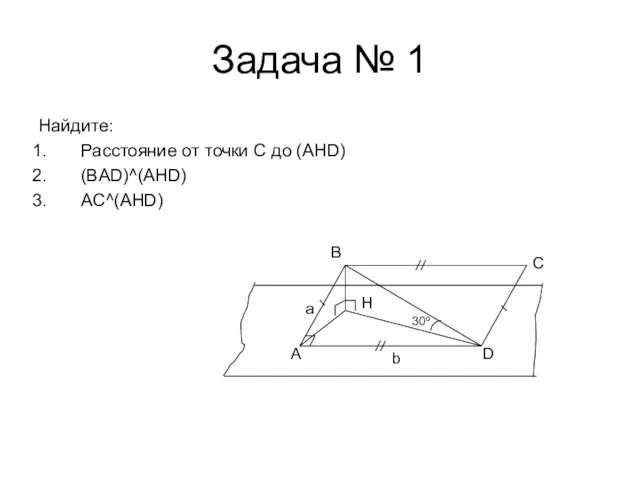
Задача № 1
Найдите:
Расстояние от точки C до (AHD)
(BAD)^(AHD)
AC^(AHD)
A
D
C
B
H
a
b
30o

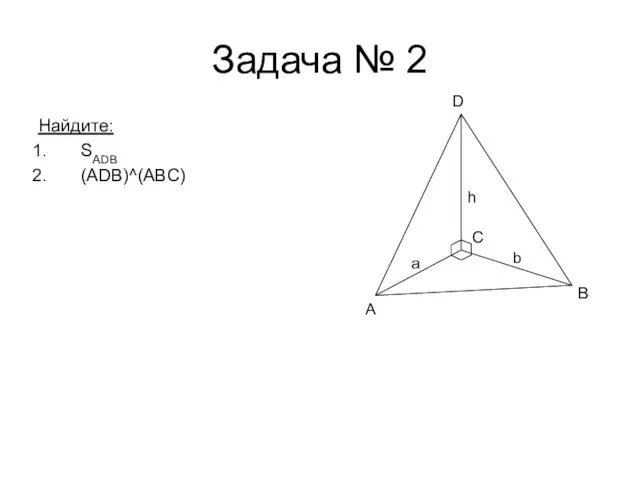
Задача № 2
Найдите:
SADB
(ADB)^(ABC)
A
B
D
h
a
C
b

Решение задач по готовым чертежам

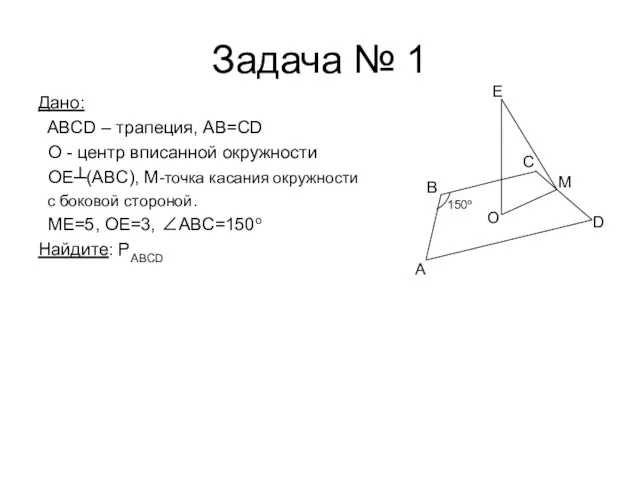
Задача № 1
Дано:
ABCD – трапеция, AB=CD
О - центр вписанной окружности
ОЕ┴(ABC), М-точка касания окружности
с боковой стороной.
ME=5, OE=3, ∠ABC=150o
Найдите: PABCD
A
D
M
O
B
C
E
150o

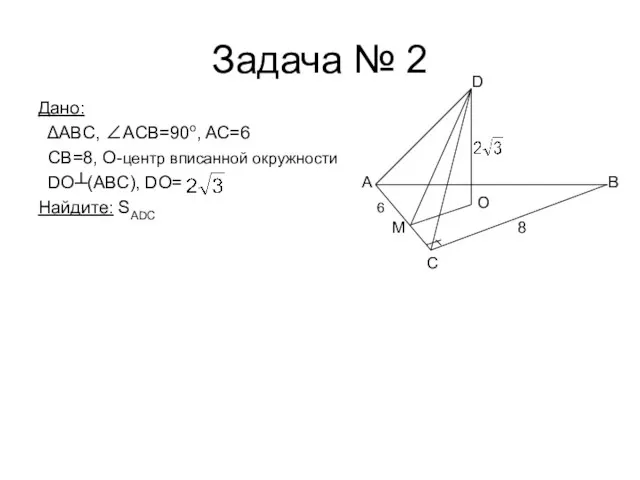
Задача № 2
Дано:
ΔABC, ∠АCВ=90o, AC=6
CB=8, O-центр вписанной окружности
DO┴(ABC), DO=
Найдите: SADC
C
B
A
D
M
O
8
6

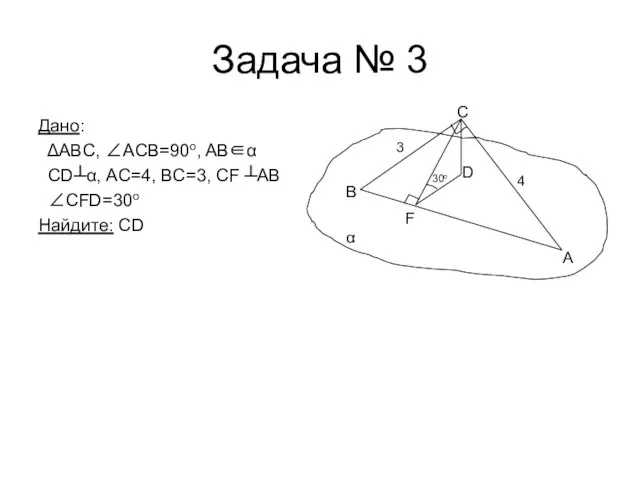
Задача № 3
Дано:
ΔABC, ∠АCВ=90o, AB∈α
CD┴α, AC=4, BC=3, CF ┴AB ∠CFD=30o
Найдите: CD
F
A
B
D
C
3
4
α
30o

Тест «Перпендикулярность»

В-1
1.Какое из следующих утверждений верно?
А: двугранным углом называется фигура, образованная прямой а и двумя полуплоскостями с общей границей а;
В: двугранный угол имеет бесконечное множество различных линейных углов;
С: градусной мерой двугранного угла называется градусная мера его линейного угла;
D: угол между пересекающимися плоскостями может быть тупым;
2. При пересечении двух плоскостей образовались двугранные углы, один из которых в два раза больше другого. Найдите градусную меру угла между плоскостями.
А: 300; В: 600; С:900; D: 1200.

3. DАВС – правильная треугольная пирамида. DО – высота пирамиды, а точка Е – середина стороны ВС. Линейным углом двугранного угла DВСО является
А: DЕО; В: DВО; С: DЕВ; D: угол не обозначен.
4. АВСDА1В1С1D1 - прямоугольный параллелепипед, О – точка пересечения диагоналей грани АВСD. Расстояние от точки С1 до диагонали ВD равно
А: С1С; В: С1О; С: С1В; D:С1D.
5. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости, а катет наклонен к этой плоскости под углом 300. найдите угол между плоскостью и плоскостью треугольника.
А: 900; В: 600; С:450; D: 300.

В-2
1.Какое из следующих утверждений верно?
А: градусная мера двугранного угла не превосходит 900;
В: двугранным углом называется угол, образованный прямой а и двумя полуплоскостями с общей границей а;
С: если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны;
D: угол между плоскостями тупой.
2. При пересечении двух плоскостей образовались двугранные углы, градусная мера одного из которых на 300 больше градусной меры другого. Найдите градусную меру угла между этими плоскостями.
А: 1050; В: 900; С:750; D: 600

3. DАВС – треугольная пирамида. DВ – высота пирамиды, а точка Е – середина стороны АС. Линейным углом двугранного угла АВDС является
А: DВА; В: DВЕ; С: АВС; D: угол не обозначен.
4. АВСDА1В1С1D1 - прямоугольная призма, Точка О1 и О –пересечения диагоналей оснований АВСD и А1В1С1D. Расстояние от точки С1 до диагонали АС равно
А: С1С; В: С1А; С: С1О; D:С1О.
5. Гипотенуза прямоугольного равнобедренного треугольника лежит в плоскости угол между плоскостью и плоскостью треугольника равен 450. Найдите градусную меру угла, под которым катет наклонен к плоскости.
А: 900; В: 600; С:450; D: 300

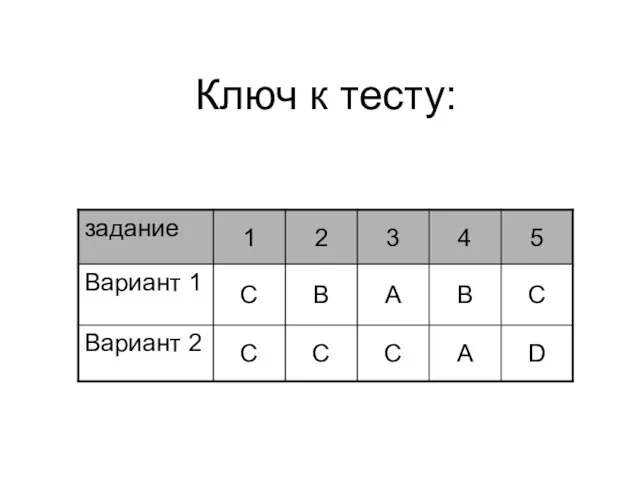
Ключ к тесту:

Итоги урока

Оценки за урок: