ПЕРСПЕКТИВЫ ПРИМЕНЕНИЯ МНОГОПОРОГОВЫХ ДЕКОДЕРОВ В ВЫСОКОСКОРОСТНЫХ СИСТЕМАХ ПЕРЕДАЧИ ДАННЫХ

Золотарёв, Овечкин
Одним из важнейших методов снижения вероятности ошибки при передаче данных по каналам с шумами является использование методов помехоустойчивого кодирования
Кодирование - это введение избыточности в передаваемое сообщение
k - информационные символы
+
r - избыточные символы
R=k/n - кодовая скорость (доля полезной информации)
n = k + r - длина кода

Золотарёв, Овечкин
ОСНОВНАЯ ЦЕННОСТЬ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ
Применение помехоустойчивого кодирования позволяет получить энергетический выигрыш,
каждый децибел которого оценивается
в миллионы долларов и позволяет:
снизить мощность передатчика;
повысить скорость передачи данных;
уменьшить размеры антенн;
повысить дальность связи;
экономить полосу пропускания;
работать при большем шуме в канале.

Золотарёв, Овечкин
КАКИМИ ДОЛЖНЫ БЫТЬ КОДЫ?
Коды должны быть:
длинными;
допускающими простое и эффективное декодирование.

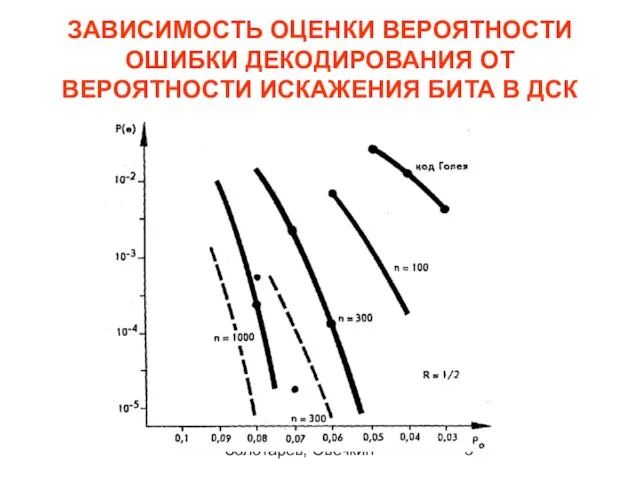
Золотарёв, Овечкин
ЗАВИСИМОСТЬ ОЦЕНКИ ВЕРОЯТНОСТИ ОШИБКИ ДЕКОДИРОВАНИЯ ОТ ВЕРОЯТНОСТИ ИСКАЖЕНИЯ БИТА В ДСК

Золотарёв, Овечкин
НАИБОЛЕЕ ЭФФЕКТИВНЫЕ КОДЫ И МЕТОДЫ ДЕКОДИРОВАНИЯ
алгоритм Витерби;
код Рида-Соломона и свёрточный код, декодируемый с помощью алгоритма Витерби;
турбо коды;
турбо коды произведения;
низкоплотностные коды;
коды повторения-накопления;
многопороговые декодеры.

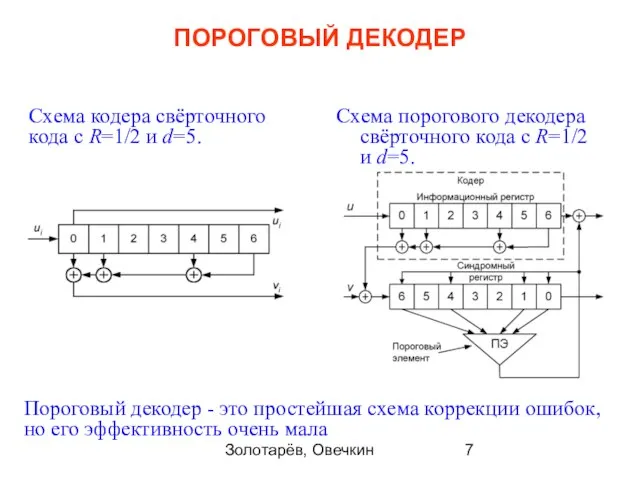
Золотарёв, Овечкин
ПОРОГОВЫЙ ДЕКОДЕР
Схема порогового декодера свёрточного кода с R=1/2 и d=5.
Пороговый декодер - это простейшая схема коррекции ошибок, но его эффективность очень мала
Схема кодера свёрточного кода с R=1/2 и d=5.

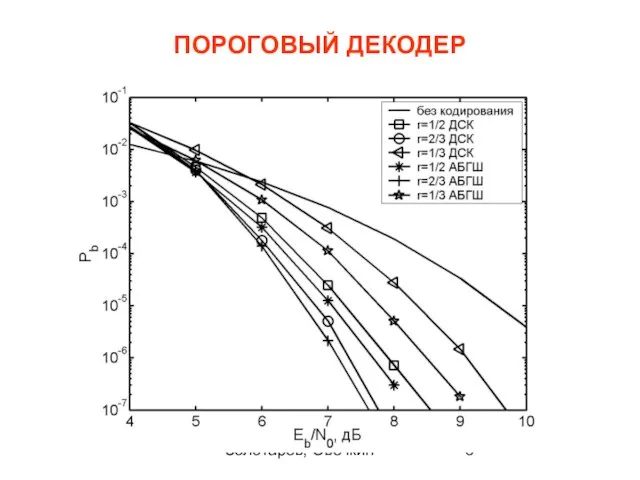
Золотарёв, Овечкин
ПОРОГОВЫЙ ДЕКОДЕР

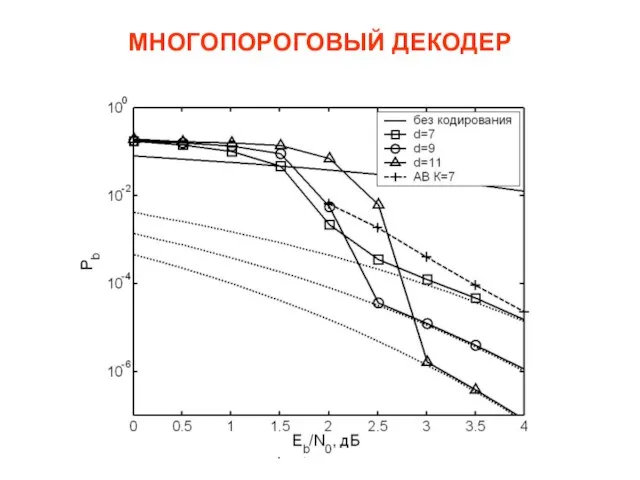
Золотарёв, Овечкин
МНОГОПОРОГОВЫЙ ДЕКОДЕР
Многопороговый декодер (МПД) является модификацией обычного порогового декодера.
В МПД впервые использовался итеративный метод декодирования, нашедший впоследствии применение в турбо кодах.
МПД многократно изменяет символы принятого сообщения и может при линейной сложности реализации достичь решения оптимального декодера.

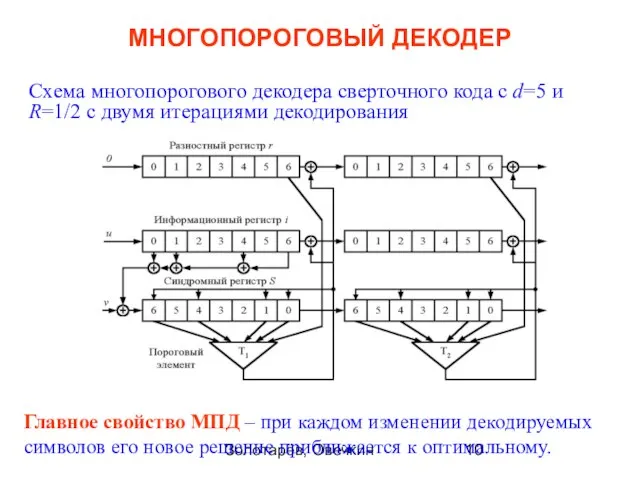
Золотарёв, Овечкин
МНОГОПОРОГОВЫЙ ДЕКОДЕР
Схема многопорогового декодера сверточного кода с d=5 и R=1/2 с двумя итерациями декодирования
Главное свойство МПД – при каждом изменении декодируемых символов его новое решение приближается к оптимальному.

Золотарёв, Овечкин
МНОГОПОРОГОВЫЙ ДЕКОДЕР

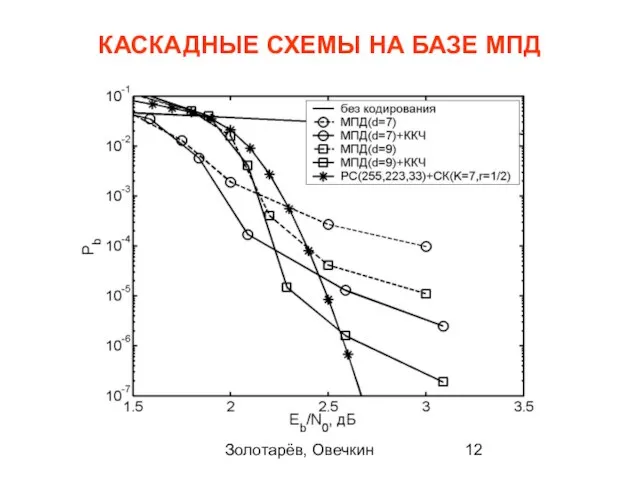
Золотарёв, Овечкин
КАСКАДНЫЕ СХЕМЫ НА БАЗЕ МПД

Золотарёв, Овечкин
1. Сложность программной реализации:
NМПД=(I+1)(d+2) операций, эквивалентных сложению на декодируемый бит, где I – число итераций, d – кодовое расстояние.
2. Применяется для кодов с d<20 при 10-20 итерациях декодирования.
3. Возможно снижение сложности до величины порядка NМПД=4d+3I.
Это более чем на порядок проще и быстрее, чем, например, при использовании турбо кодов!
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ МПД

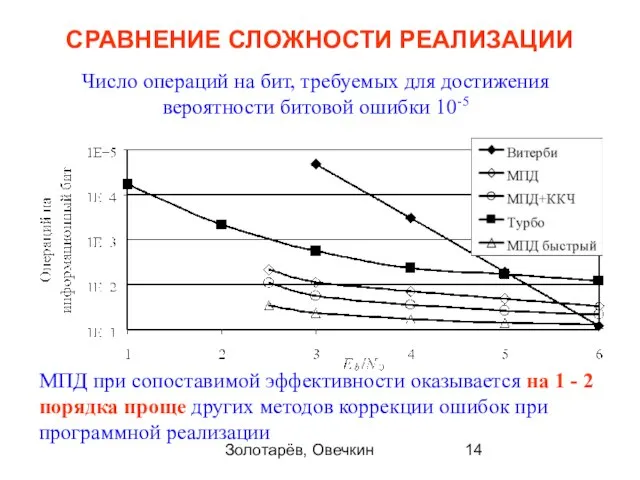
Золотарёв, Овечкин
СРАВНЕНИЕ СЛОЖНОСТИ РЕАЛИЗАЦИИ
МПД при сопоставимой эффективности оказывается на 1 - 2 порядка проще других методов коррекции ошибок при программной реализации
Число операций на бит, требуемых для достижения вероятности битовой ошибки 10-5

Золотарёв, Овечкин
АППАРАТНАЯ РЕАЛИЗАЦИЯ МПД НА ПЛИС
1. МПД состоит почти полностью из элементов памяти или регистров сдвига. Это наиболее быстрые элементы ПЛИС и БИС. Доля остальных элементов МПД много менее 1%.
2. МПД состоит из 3 - 40 параллельно работающих регистров сдвига и однотактных пороговых элементов с мгновенной реализацией своих функций. Именно поэтому МПД для некоторых значений параметров примерно на 2 и более порядков быстрее, чем, например, турбо декодеры.
3. Характеристики аппаратной реализации МПД:
Скорость – 160 - 480 Мбит/с и более,
ЭВК = 6,5 - 8,5 дБ.

Золотарёв, Овечкин
ЧИПСЕТ МПД ДЕКОДЕРА НА ПЛИС XILINX

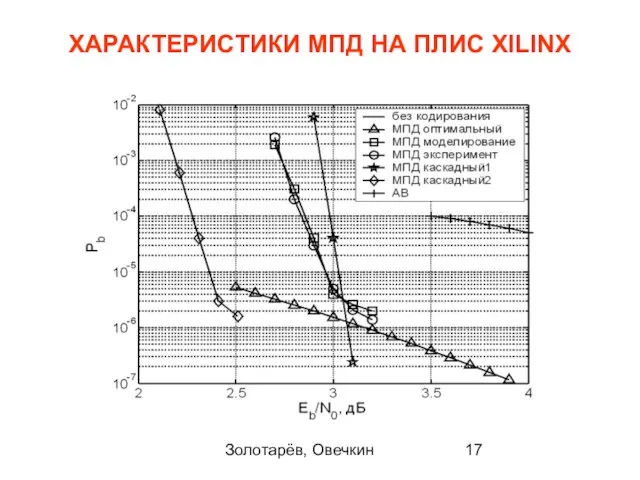
Золотарёв, Овечкин
ХАРАКТЕРИСТИКИ МПД НА ПЛИС XILINX