Содержание
- 2. Содержание Открытие первообразной Понятие первообразной Основное свойство первообразной Три правила нахождения первообразной Интегралы Неопределенный интеграл Используемая
- 3. Открытие первообразной В математике важнейшей заслугой Готфрида Лейбница и Исаака Ньютона является разработка дифференциального и интегрального
- 4. Понятие первообразной Функция F называется первообразной для функции f на заданном промежутке, если для всех x
- 5. Основное свойство первообразной Любая первообразная для функции f на промежутке I может быть записана в виде
- 6. Три правила нахождения первообразных Правило 1. Если F есть первообразная для f, а G-первообразная для g,
- 7. Интегралы Первообразные важны тем , что позволяют вычислять интегралы . Если F – первообразная интегрируемой функции
- 8. Неопределенный интеграл Множество первообразных данной функции f называют неопределенным интегралом f и записывают в виде интеграла
- 10. Скачать презентацию







 Welcome to Krasnoyarsk
Welcome to Krasnoyarsk Живопись авангарда
Живопись авангарда  Debate club
Debate club Подача декларации о сделке с древесиной со стороны покупателя
Подача декларации о сделке с древесиной со стороны покупателя Сила тока. Измерение силы тока
Сила тока. Измерение силы тока Презентация на тему Категории товаров, в отношении которых законодательством ТС установлено лицензирование экспорта или импорта
Презентация на тему Категории товаров, в отношении которых законодательством ТС установлено лицензирование экспорта или импорта  Неизвестное об известных
Неизвестное об известных Сергей Есенин
Сергей Есенин Педагогический совет
Педагогический совет Литература русского зарубежья
Литература русского зарубежья Моя президентская программа. Если бы я была президентом
Моя президентская программа. Если бы я была президентом Испытательные культуры – это лесные культуры, создаваемые по специальным методикам семенным потомством плюсовых деревьев,
Испытательные культуры – это лесные культуры, создаваемые по специальным методикам семенным потомством плюсовых деревьев,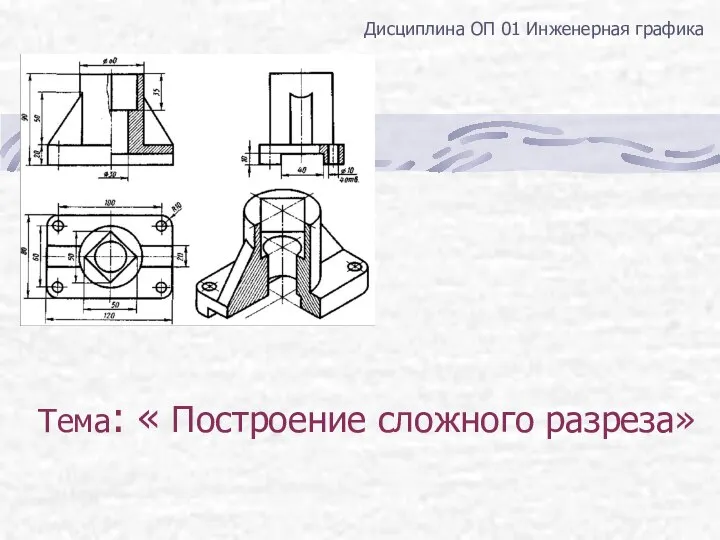 Построение сложного разреза на чертежах
Построение сложного разреза на чертежах Повторение и систематизация изученного в 6 классе
Повторение и систематизация изученного в 6 классе Узлы ЭВМ
Узлы ЭВМ Презентация на тему Люксметр
Презентация на тему Люксметр  Дочь политрука
Дочь политрука бкласс
бкласс Наркотики. Я против! А вы?
Наркотики. Я против! А вы? Межкультурное общение с гостем из Монголии
Межкультурное общение с гостем из Монголии 7a_19_09_22g
7a_19_09_22g Дж. К Ролинг
Дж. К Ролинг Применение Цифровых Образовательных Ресурсов (ЦОР) на уроках физики
Применение Цифровых Образовательных Ресурсов (ЦОР) на уроках физики 24 мая День славянской письменности и культуры
24 мая День славянской письменности и культуры Квалифицированные кадры для сельхозтоваропроизводителей
Квалифицированные кадры для сельхозтоваропроизводителей Финансы организаций
Финансы организаций Патогенез лихорадки
Патогенез лихорадки ТЕМА 4: Анализ финансовой устойчивости и платежеспособности
ТЕМА 4: Анализ финансовой устойчивости и платежеспособности