Решение уравнений содержащих неизвестную под знаком модуля

ВНИМАНИЕ!
При использовании наших материалов помните о соблюдении авторских прав!

Объект исследования:
Предмет исследования:
решение уравнений, содержащих неизвестную под знаком модуля
способы решения уравнений
Цель работы:
ознакомление учащихся с теоретическими основами решения уравнений с модулем, рекомендациями к решению, алгоритмирование процесса решения уравнений содержащих неизвестную под знаком модуля

Работа с литературными источниками.
2) Математическое моделирование постановки задачи для построения графического образа линий, входящих в данное уравнение.
3) Эксперимент: исследование различных подходов и методов решения уравнений; исследование изменения вида кривой, в зависимости от параметров входящих в её уравнение .
Методы исследования:

ВВЕДЕНИЕ
ГЛАВА 1. Решение уравнений.
1.1.Определение модуля. Решение по определению
1.2. Решение уравнений по правилам
1.3. Задачи с несколькими модулями. Последовательное и параллельное раскрытие модулей
1.4. Метод интервалов в задачах с модулями
1.5. Вложенные модули
1.6. Модули и квадраты
1.7. Модули неотрицательных выражений
ГЛАВА 2. Функционально-графический способ решения задач.
2.1. Графики простейших функций, содержащих знак абсолютной величины
2.2. Построение графиков уравнений, содержащих знак модуля
2.3. Графическое решение уравнений, содержащих знак модуля
2.4. Графическое решение задач с параметром и модулем
ЗАКЛЮЧЕНИЕ
ЛИТЕРАТУРА
ПРИЛОЖЕНИЕ. Исследование вида графического образа заданного неравенством , в зависимости от параметров a и b
Содержание работы

1.1.Определение модуля. Решение по определению.
По определению, модуль, или абсолютная величина, неотрицательного числа a совпадает с самим числом, а модуль отрицательного числа равен противоположному числу, то есть – a:
Запишем решение простейших уравнений в общем виде:
Пример. Решить уравнение |x –3| = 3 – 2x.
Рассматриваем два случая.
При x – 3> 0 уравнение принимает вид x – 3 = 3 – 2x, откуда x = 2. Но это значение не удовлетворяет неравенству x – 3 > 0, потому не входит в ответ исходного уравнения.
При x – 3 < 0 получаем 3 – x = 3 – 2x и x = 0. Этот корень удовлетворяет соответствующему условию x – 3 < 0.
Итак, ответ к исходному уравнению: x = 0.
Ответ: х = 0.

2-е правило: |f(x)| = g(x) ⇔
1-е правило: |f(x)| = g(x) ⇔
ЗАМЕЧАНИЕ. Фигурные скобки обозначают системы, а квадратные – совокупности.
Решения системы уравнений – это значения переменной, одновременно удовлетворяющие всем уравнениям системы.
Решениями совокупности уравнений являются все значения переменной, каждое из которых есть корень хотя бы одного из уравнений совокупности.
1.2. Решение уравнений по правилам

Пример . Решить уравнение |x2 – x – 6| = |2x2 + x – 1|.
Решение. Мы уже знаем, что рассматривать (целых 4) варианта распределения знаков выражений под модулями здесь не нужно: это уравнение равносильно совокупности двух квадратных уравнений без каких-либо дополнительных неравенств:
Которая равносильна:
Первое уравнение совокупности решений не имеет (его дискриминант отрицателен), второе уравнение имеет два корня .
Ответ:

Третий способ освобождения от модуля –
замена переменной
Пример . Решить уравнение:
Решение. Заметим, что , тогда уравнение примет вид:
Пусть , тогда решим квадратное уравнение:
Его корни , условию удовлетворяет первый корень.
Возвращаясь к переменной х, получаем уравнение
решая которое находим:
Ответ: .

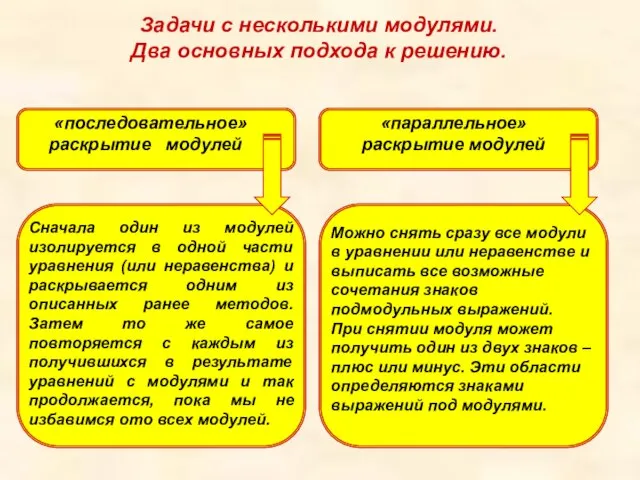
Задачи с несколькими модулями.
Два основных подхода к решению.
Сначала один из модулей изолируется в одной части уравнения (или неравенства) и раскрывается одним из описанных ранее методов. Затем то же самое повторяется с каждым из получившихся в результате уравнений с модулями и так продолжается, пока мы не избавимся ото всех модулей.
Можно снять сразу все модули в уравнении или неравенстве и выписать все возможные сочетания знаков подмодульных выражений. При снятии модуля может получить один из двух знаков – плюс или минус. Эти области определяются знаками выражений под модулями.
«последовательное»
раскрытие модулей
«параллельное» раскрытие модулей

Решение.
Уединим второй модуль и раскроем его, пользуясь первым способом, то есть просто определением абсолютной величины:
К полученным двум уравнениям применяем второй способ освобождения от модуля:
Наконец, решаем получившиеся четыре линейных уравнения и отбираем те их корни, которые удовлетворяют соответствующим неравенствам :
1способ

Лишь первый и третий из этих корней удовлетворяют соответствующим неравенствам, а значит, и исходному уравнению.
2способ
Решение.
Рассмотрим 4 возможных набора знаков выражений под модулями.

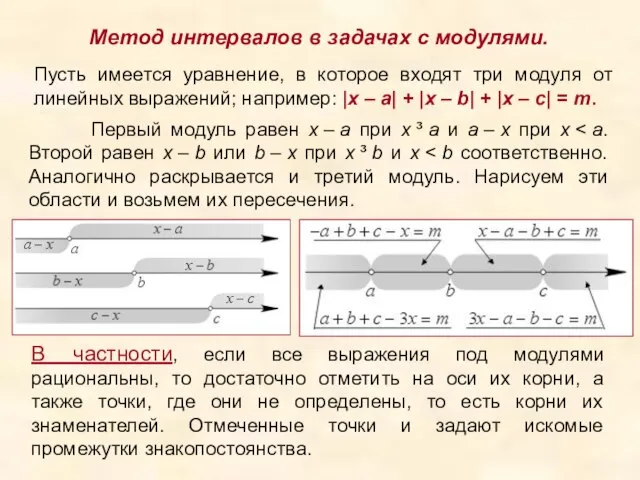
Метод интервалов в задачах с модулями.
Пусть имеется уравнение, в которое входят три модуля от линейных выражений; например: |x – a| + |x – b| + |x – c| = m.
Первый модуль равен x – a при x ³ a и a – x при x < a. Второй равен x – b или b – x при x ³ b и x < b соответственно. Аналогично раскрывается и третий модуль. Нарисуем эти области и возьмем их пересечения.
В частности, если все выражения под модулями рациональны, то достаточно отметить на оси их корни, а также точки, где они не определены, то есть корни их знаменателей. Отмеченные точки и задают искомые промежутки знакопостоянства.

.
Решение.
Найдем нули функции x+2=0 или x+3=0 , откуда x=-2 , x=-3. Рассмотрим 3 возможных набора знаков выражений под модулями.
Решаем задачу на каждом интервале:
Итак, данное уравнение не имеет решений.

Вложенные модули
Последовательное раскрытие модулей наиболее эффективно в "задачах-матрешках", где внутри одного модуля находится другой, а то и несколько.
Решение.
Освободимся от внешнего модуля, получим:

Модули и квадраты
Он основан на двух очевидных соображениях. Во-первых, из двух неотрицательных чисел то больше, квадрат которого больше, а если квадраты равны, то и числа равны: a > b ⇔ a2 > b2; a = b ⇔ a2 = b2.
Во-вторых, квадрат модуля числа равен квадрату самого числа: |a|2 = a2. Поэтому допускается такое равносильное преобразование:

Модули неотрицательных выражений.
Решение.
Нетрудно догадаться, что все выражения, стоящие под знаком второго, третьего и т.д. модулей положительны. И поскольку модуль положительного выражения равен самому этому выражению, получим

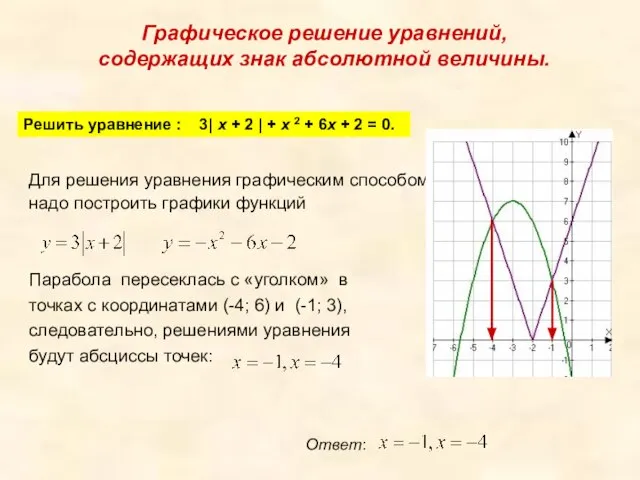
Графическое решение уравнений,
содержащих знак абсолютной величины.
Решить уравнение : 3| x + 2 | + x 2 + 6x + 2 = 0.

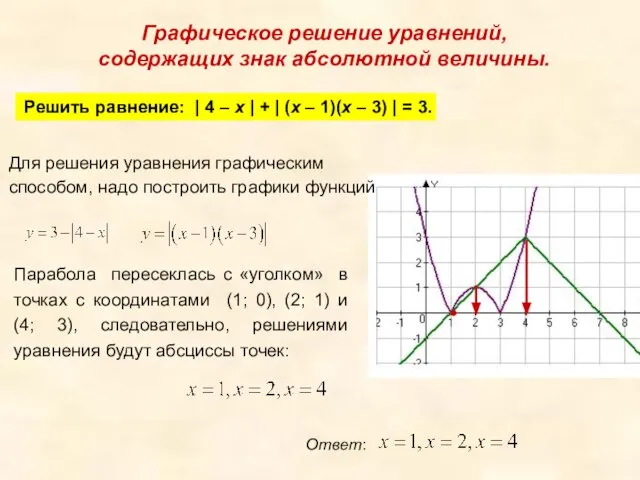
Графическое решение уравнений,
содержащих знак абсолютной величины.
Решить равнение: | 4 – x | + | (x – 1)(x – 3) | = 3.
Для решения уравнения графическим способом, надо построить графики функций
Парабола пересеклась с «уголком» в точках с координатами (1; 0), (2; 1) и (4; 3), следовательно, решениями уравнения будут абсциссы точек:

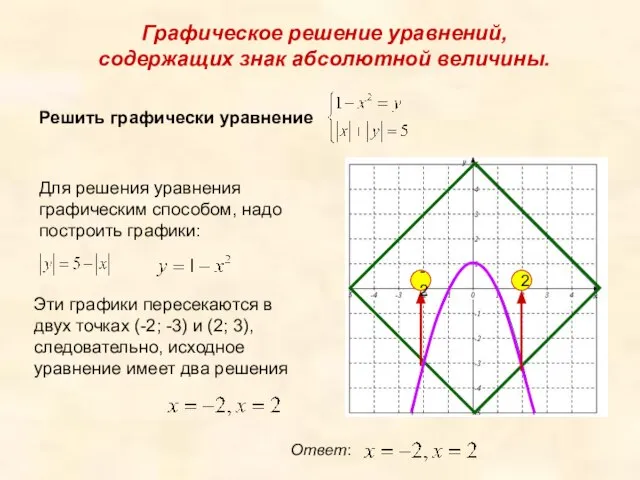
Графическое решение уравнений,
содержащих знак абсолютной величины.
Решить графически уравнение

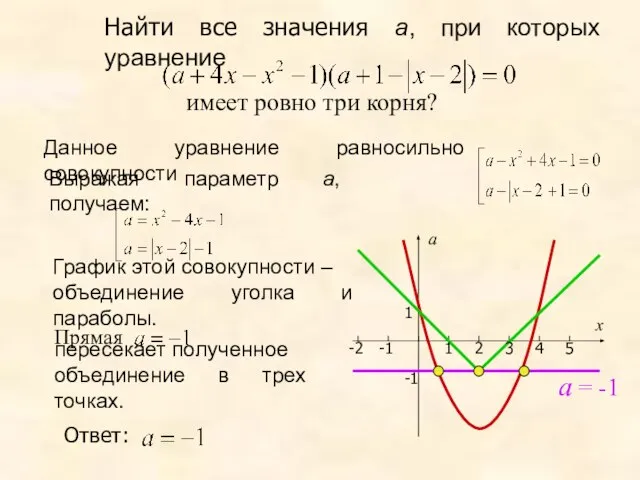
Найти все значения а, при которых уравнение
Данное уравнение равносильно совокупности
Выражая параметр а, получаем:
График этой совокупности –
объединение уголка и параболы.
пересекает полученное
объединение в трех точках.
имеет ровно три корня?
Ответ:
1
2
3
4
5
-1
-2
-1
1
х
а
а = -1
Прямая