Теорема Пифагора и способы её доказательства

Cуть истины вся в том, что нам она – навечно,
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорно безупречна…
Шамиссо

«Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…»
Теорема Пифагора
красота
простота
значимость
Иоганн Кеплер

Цель:
Рассмотреть классические и малоизвестные доказательства теоремы Пифагора
Познакомиться с областями применения теоремы и с фактами истории открытия теоремы Пифагора
Сделать выводы о значимости теоремы Пифагора

Пифагор Самосский
(570-500 гг. до н.э.)

Некоторые факты из жизни Пифагора:
Родился на о.Самосе около 570 г. до н.э.
Учился во многих городах мира у великих учёных- Ферекида, Фалеса, Гермодаманта…
В Египте Пифагор попал в персидский плен,где пробыл 12 лет
В Кротоне(Италия) учредил «Пифагорейскую школу»

РАЗЛИЧНЫЕ СПОСОБЫ
ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРА

Формулировка теоремы Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c
a
b

ДОКАЗАТЕЛЬСТВО,
основанное на равновеликости фигур:
«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах».

Алгебраический метод доказательства теоремы:
c
c
c
c
a
a
a
a
b
b
b
b
Пусть F- прямоугольный треугольник со сторонами a,b и c,а Q- квадрат со стороной с.
SABCD= 4S▲ + SQ=
= 4·1/2 ab +c2 =
= 2 ab + c2
SABCD= (а+b)2 = a2 + 2ab +b2
2 ab + c2 =a2 + 2ab +b2
=> c2 = a 2 +b 2
A
B
D
C
F
F
F
F
F
Q

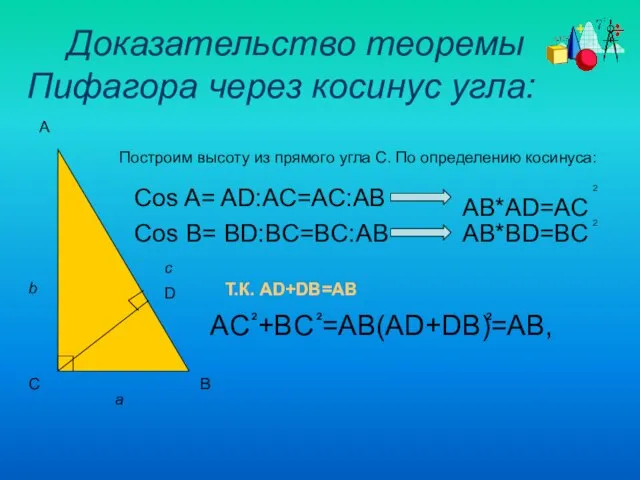
Доказательство теоремы Пифагора через косинус угла:
D
A
C
B
c
a
b
Построим высоту из прямого угла С. По определению косинуса:
Cos A= AD:AC=AC:AB
2
AB*AD=AC
Сos B= BD:BC=BC:AB
AB*BD=BC
2
Т.К. AD+DB=AB
AC +BC =AB(AD+DB)=AB,
2 2 2

Векторное доказательство
теоремы:
АВС - прямоугольный треугольник, построенный на векторах.
b+c=a c = a - b
c²=a²+b²-2ab
Т.к. a b, то ab=0, c²=a²+b² или c²=a²+b²

Доказательство Гарфилда:
ABC-прямоугольный треугольник
1)CD =AВ; ED=АС; ЕD AD
2) SABED=2*AB*AC/2+BC/ 2 3) SABED=(DE+AB)*AD/2.
4) AB*AC+BC /2=(DE+AB)(CD+AC)/2
AB*AC+BC /2= (AC+AB) /2
AB*AC+BC/2= AC/2+AB/2+AB*AC
BC=AB+AC
2
2
2
2
2
2
2
2
2
2

Пусть катеты прямоугольных ▲-ков d равны a и b, а гипотенуза – с.
Тогда (a − b) +(4ab)/2= с, то есть
ДОКАЗАТЕЛЬСТВО БХАСКАРИ-АЧАРНА:
С
С
С
С
d
d
d
d
2
2
a
a
a
a
b
b
b
b

ABC-прямоугольный ▲ повернем на 90° так, чтобы он занял положение A'CB'.
▲ A'АВ'В : AA’C=b²/2
SCBB'=a²/2
SA'AB'B=(a²+b²)/2
▲ A'В'А и ▲ A'В'В: DA и DB-общие,
SA'AB'B=c*DA/2+ c*DB/2=c(DA+DB)/2=c²/2
Сравнивая полученные выражения:
(a²+b²)/2= c²/2 a²+b²=c²
Доказательство Хоукинса:
С
1.
2.
С

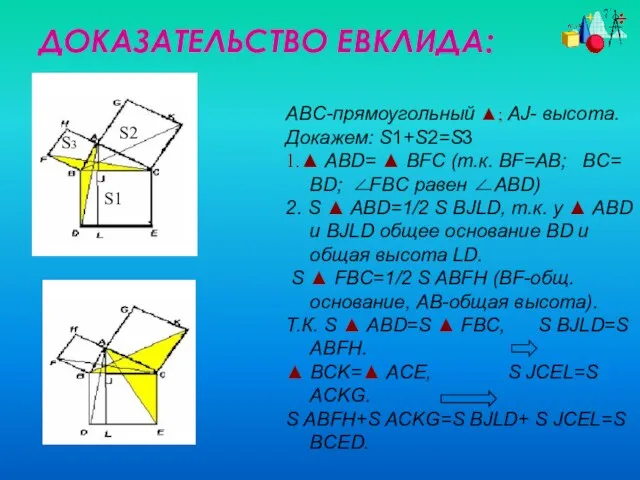
ABC-прямоугольный ▲; AJ- высота.
Докажем: S1+S2=S3
1.▲ ABD= ▲ BFC (т.к. BF=AB; BC= BD; FBC равен ABD)
2. S ▲ ABD=1/2 S BJLD, т.к. у ▲ ABD и BJLD общее основание BD и общая высота LD.
S ▲ FBC=1/2 S ABFH (BF-общ.основание, AB-общая высота).
Т.К. S ▲ ABD=S ▲ FBC, S BJLD=S ABFH.
▲ BCK=▲ ACE, S JCEL=S ACKG.
S ABFH+S ACKG=S BJLD+ S JCEL=S BCED.
.
ДОКАЗАТЕЛЬСТВО ЕВКЛИДА:
S3
S2
S1

Области применения теоремы Пифагора
архитектура
мобильная связь
астрономия
литература
вычисление длин отрезков
некоторых
фигур на плоскости

Знаменитый египетский
треугольник
3, 4,5-одна из
Пифагоровых
троек

Теорема Пифагора- живительный источник красоты, совершенства и творчества для новых поколений!