РЕАЛЬНЫЕ ГАЗЫ

4.1. СВОЙСТВА РЕАЛЬНЫХ ГАЗОВ

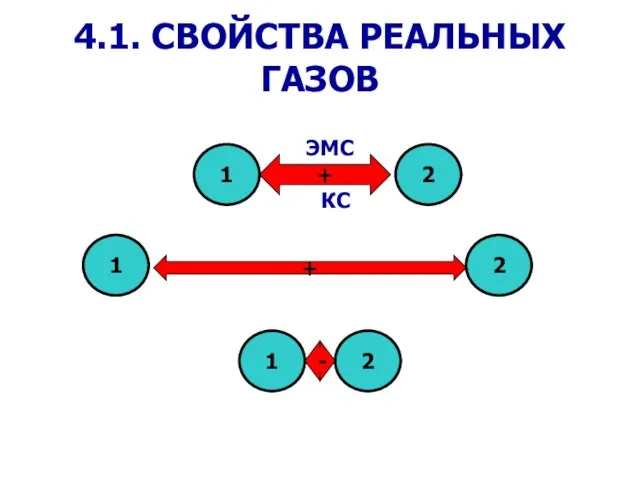
Из-за наличия сил взаимодействия между молекулами и конечности их объема законы идеальных газов ни при каких условиях не могут быть строго применимы к реальным газам.
С - Коэффициент сжимаемости выражает отклонение свойств реального газа от свойств идеального

- число Амага
Температура, соответствующая изотерме с точкой минимума на оси ординат (p = 0), называется температурой Бойля.
Свойства реальных газов как в количественном, так и качественном отношениях значительно отличаются от свойств идеальных газов. Поэтому все результаты, полученные для реальных газов на основе законов идеальных газов, нужно рассматривать как приближенные и справедливые при очень больших разрежениях (p → 0)

Уравнение Боголюбова - Майера
вириальные коэффициенты, выражаются через потенциальную энергию взаимодействия молекул данного газа и температуру Т, a υ = 2, 3, 4, ...— порядковый номер вириального коэффициента.

4.2. УРАВНЕНИЕ СОСТОЯНИЯ ВАН-ДЕР-ВААЛЬСА
Поправки, которые учитывают отклонение реального газа от идеального:
первая поправка, зависящая от объема самих молекул

Вторая поправка учитывает влияние сил взаимодействия между молекулами
Поправка Δp прямо пропорциональна как числу притягиваемых, так и числу притягивающих молекул, или прямо пропорциональна квадрату плотности газа, или обратно пропорциональна квадрату его удельного объема:
а — коэффициент пропорциональности, принимающий для каждого газа определенное числовое значение, не зависящее от параметров состояния

Уравнение Ван-дер-Ваальса (1873 г.)
внутреннее давление
(для воды при температуре 293 К а/v2 ≈ 1080 МПа)
Уравнение Ван-дер-Ваальса качественно верно отображает поведение реальных веществ в жидком или газообразном состоянии.
Для двухфазных состояний (пар и вода) оно неприменимо.
(4.1)
Для 1 моль газа

Основные частные производные параметров для реального газа из уравнения Ван-дер-Ваальса:

4.3. АНАЛИЗ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА
- уравнение третьей степени относительно удельного объема газа
1) все три корня различны и действительны;
2) все три корня действительны и равны между собой;
3) один корень действительный и два мнимых (комплексных) [реальное значение имеет только один действительный корень].

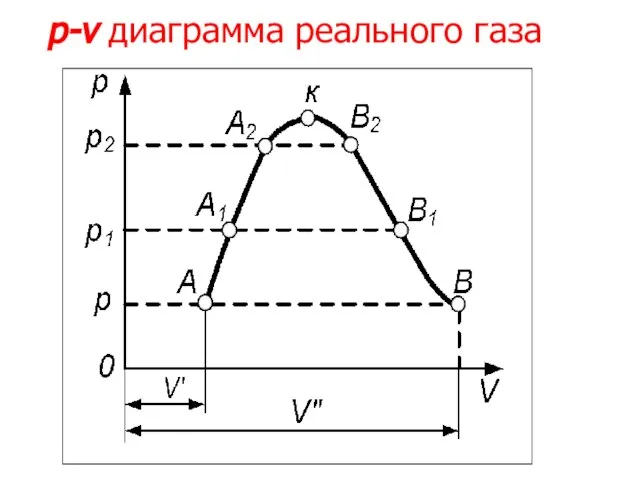
Прямая АВ, пересекающая такого типа изотерму, дает три действительных значения удельного объема в точках A, R и В, т. е. эти изотермы соответствуют первому случаю решения уравнения Ван-дер-Ваальса (три различных действительных корня).
При определенной температуре, называемой критической, изотерма уравнения Ван-дер-Ваальса не будет иметь волнообразного участка. На этой изотерме есть точка перегиба, касательная к которой должна быть горизонтальной. Это соответствует второму случаю решения уравнения Ван-дер-Ваальса, когда все три корня действительны и равны между собой (рис. 4.3, точка К).
При температурах T > Tк имеет место третий случай решения уравнения Ван-дер-Ваальса, когда один корень действительный, а два мнимых.

Кривую АК, на которой жидкость находится в состоянии кипения, называют пограничной кривой жидкости (нижней пограничной кривой);
кривая ВК, называемая пограничной кривой пара (верхней пограничной кривой), представляет собой совокупность состояний сухого насыщенного пара.

Таким образом, для реального вещества рv-диаграмму можно разбить на три характерные области:
1) область жидкого состояния, расположенную левее пограничной кривой жидкости;
2) область двухфазных состояний (влажного пара), расположенную между пограничными кривыми жидкости и пара;
3) область перегретого пара, расположенную правее пограничной кривой пара и выше критической точки.
рv - диаграмму реального вещества называют диаграммой Эндрюса (1869 г).

p-v диаграмма реального газа

Критическое состояние вещества (Менделеев, 1861 г)
Критической температурой называют абсолютную температуру кипения, при которой поверхностное натяжение в жидкости становится равным нулю, т. е. исчезает различие между жидкостью и парообразным состоянием вещества (насыщенным паром).
Из анализа уравнения Ван-дер-Ваальса применительно к критическому состоянию можно:
получить выражение критических параметров через константы уравнения а и b ;
определить константы а и b при известных критических параметрах.

(а)
(б)
(в)
(г)
(4.2)
(4.4)
(4.3)
Критические параметры выраженные через константы уравнения а и b :

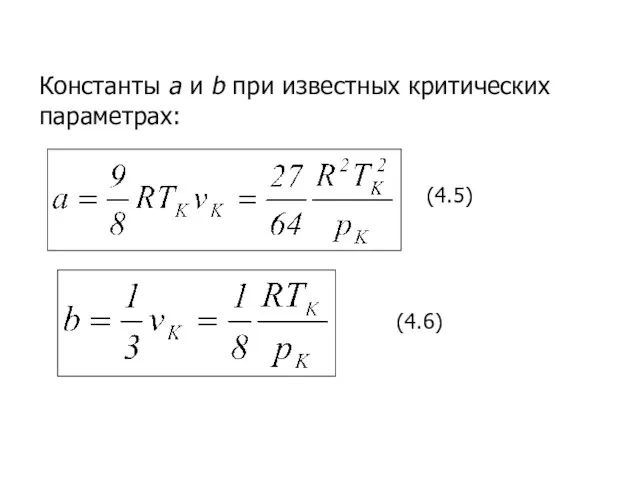
Константы а и b при известных критических параметрах:
(4.5)
(4.6)

Уравнение Ван-дер-Ваальса в приведенных параметрах состояния.
приведенное уравнение.
Оно не включает никаких величин, характеризующих данное вещество, поэтому уравнение справедливо для любого вещества, которое подчиняется уравнению Ван-дер-Ваальса. Состояния веществ, находящихся при одинаковых π, φ и τ, называются соответственными состояниями.
(4.7)

Закон соответственных состояний
В критической точке все три приведенных параметра имеют одинаковое значение, равное единице, и критические состояния всех веществ являются соответственными.
Если два вещества имеют одинаковые два параметра из трех приведенных, то и третий параметр у этих веществ будет иметь одинаковое значение и вещества будут находиться в соответственных состояниях. Указанное явление носит название закона соответственных состояний.
Этот закон служит для определения свойств вещества, если известны свойства другого вещества, находящегося с ним в соответственном состоянии. Такое определение свойств вещества называется методом термодинамического подобия.

Критический коэффициент
Для всех термодинамических подобных веществ, подчиняющихся уравнению Ван-дер-Ваальса, критический коэффициент должен иметь постоянное значение

4.4. УРАВНЕНИЕ СОСТОЯНИЯ ДЛЯ РЕАЛЬНЫХ ГАЗОВ М. П. ВУКАЛОВИЧА И И. И. НОВИКОВА
а и b — постоянные уравнения Ван-дер-Ваальса (для водяного пара а=620 Нм4/кг2, b=0,0009 м3/кг;
С и m — постоянные, определяемые на основании опытных данных (для водяного пара С=405000 (м3·град)/кг, m=1,968).
(4.8)

Дифференциальное уравнение состояния:
(4.9)
Соотношение (4.9) дает возможность установить величины, измеряемые достаточно точно на практике, и имеют важное значение для характеристики свойств реальных тел.

Отношение частной производной
к объему V характеризует скорость изменения объема при нагревании, если давление остается постоянным.
Это отношение называют температурным коэффициентом объемного расширения тела:
(4.10)