Первый закон термодинамики

1. Два принципа первого закона термодинамики
Первый закон термодинамики является частным случаем всеобщего
закона о превращении и сохранении энергии применительно к
тепловым процессам.
Первый закон термодинамики состоит из двух принципов (начал).
Первый закон называется принципом эквивалентности теплоты
и работы.
Теплота Q и работа L преобразовываются друг в друга в строго
эквивалентном соотношении:
Второй принцип гласит – теплота, сообщенная телу (системе)
расходуется на изменение его внутренней энергии и на совершение
работы этим телом (системой).

Примечание. В данном уравнении и в дальнейшем удобнее расчет
вести на единицу вещества – кг, м3, моль. Поэтому расчетные
величины обозначаются прописными буквами, а не заглавными,
при этом необходимо помнить, что для удобства и сокращения
термин «удельная» опускается, но подразумевается. Например,
в предыдущем уравнении
Q – теплота, подведенная к 1кг вещества, Дж/кг;
U1, U2 – начальная и конечная внутренняя энергия тела, отнесенная
к 1кг вещества, Дж/кг;
∆U – изменение внутренней энергии 1кг вещества, Дж/кг;
l – работа, совершенная 1кг вещества (в данном случае газа), Дж/кг.

2. Внутренняя энергия газа
Внутренняя энергия – это сумма кинетических энергий частиц
(молекул, атомов) газа и зависит она только от температуры – т.е.
интенсивности движения частиц газа, что и определяет их тепловое состояние.
Для расчетов не столь важно знать, какова внутренняя энергия газа,
а важно знать, на сколько она изменяется.

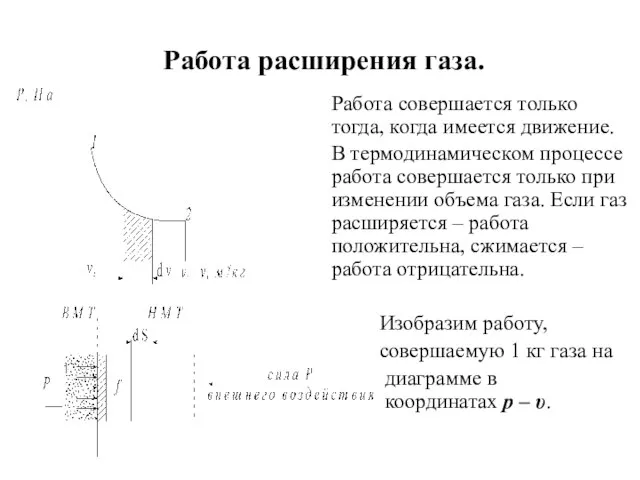
Работа расширения газа.
Работа совершается только тогда, когда имеется движение.
В термодинамическом процессе работа совершается только при изменении объема газа. Если газ расширяется – работа положительна, сжимается – работа отрицательна.
Изобразим работу,
совершаемую 1 кг газа на
диаграмме в
координатах p – υ.

Пусть в процессе 1-2 поршень перемещается из положения 1 – верхней мертвой точки (ВМТ) в положение 2 – нижней мертвой точки и преодолевает силу Р внешнего воздействия под давлением р рабочего тела. При этом газ расширяется от υ1 до υ2, оказывая давление р на днище поршня площадью f. Работа всегда определяется произведением силы Р на перемещение S.
Тогда элементарная работа dl при перемещении на элементарном отрезке dS будет равна:

Учитывая, что fdS=dv, работа расширения газа на всем участке от v1 до v2 будет равна:
При р = const l=p(v2-v1);
При v=const l=0.

3. Энтальпия газа
Энтальпия газа h, Дж/кг равна сумме внутренней
энергии газа и произведения давления на объем.
Физический смысл величины pv понятен из рисунка – это
потенциальная энергия сжатого газа. Она уравновешивает
воздействие потенциальной энергии гири и поршня, поднятых на
высоту H по отношению к днищу поршня.

Изменение энтальпии равно:
Учитывая, что
получим:
После интегрирования в пределах от Т1 до Т2 получим:

Энтропия газа
Не всегда количество подведенной можно определить через
изменение температуры тела. Например, вода кипит, а ее
температура остается постоянной. В выражении первого закона
термодинамики:
выражение не является полным дифференциалом, поскольку
неизвестна зависимость изменения р от температуры Т.
(1)

Если количество подведённой теплоты не характеризуется
соответствующим изменением температуры, то выражение (1)
можно превратить в полный дифференциал, если его левую и
правую часть разделить на температуру тела Т.
Умножив и разделив второе слагаемое на υ, получим: