Пифагор! И его достижения в геометрии!

Пифагор – самая загадочная личность, человек-символ, философ, пророк.
Пифагор – едва ли не самый популярный ученый за всю историю человечества. Ни одно имя ученого не повторяется так часто.

Великий ученый Пифагор родился около 570 г. до н.э. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Когда отец Пифагора был в Дельфах по своим торговым делам, он и его жена Партенис решили спросить у Дельфийского оракула, будет ли Судьба благоприятствовать им во время обратного путешествия в Сирию. Пифия (прорицательница Аполлона), сидя на золотом триоде над сияющим отверстием оракула, не ответила на их вопрос, но сказала Мнесарху, что его жена носит в себе дитя и что у них родится сын, который превзойдет всех людей в красоте и мудрости и который много потрудится в жизни на благо человечества.
По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.

Если дан нам треугольник И притом с прямым углом, То квадрат гипотенузы Мы всегда легко найдем : Катеты в квадрат возводим, Сумму степеней находим — И таким простым путем К результату мы придем.

Теорема Пифагора – важнейшее утверждение геометрии. Ее открытие приписывают древнегреческому философу и математику Пифагору Самосскому (VI в. до н.э.). Но изучение вавилонских клинописных таблиц и древних китайских рукописей (копий ещё более древних манускриптов) показало, что знаменитая теорема была известна задолго до Пифагора, возможно, за несколько тысячелетий до него. Заслуга же Пифагора состояла в том, что учёный первым открыл доказательство этой теоремы. Открытие теоремы Пифагором окружено множеством красивых легенд.

ТЕОРЕМА ПИФАГОРА И СПОСОБЫ ЕЁ ДОКАЗАТЕЛЬСТВА
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Различные способы доказательства теоремы Пифагора
На рисунке дан простейший равнобедренный прямоугольный треугольник АВС (закрашен серым цветом, АВ и ВС -катеты).
Если квадраты отложить в общую часть полуплоскостей с границами АВ и ВС, то сумма числовых значений площадей квадратов, построенных на катетах, равна 4SABC (квадраты совпали). Но и площадь квадрата, построенного на гипотенузе, тоже равна 4SABC
Если же квадраты отложить на сторонах во внешнюю область, то и в этом случае 2+2=4.
Теорема доказана.
Простейшее доказательство

Доказательство Эйнштейна
Точки E, C и F лежат на одной прямой; это следует из несложных расчётов градусной меры угла ECF (он развёрнутый).
CD проводим перпендикулярно EF.
Продолжены вверх левая и правая стороны квадрата, построенного на гипотенузе, до пересечения с EF; продолжена сторона ЕА до пересечения с CD.
Соответственно равные треугольники одинаково пронумерованы.

Доказательство Евклида
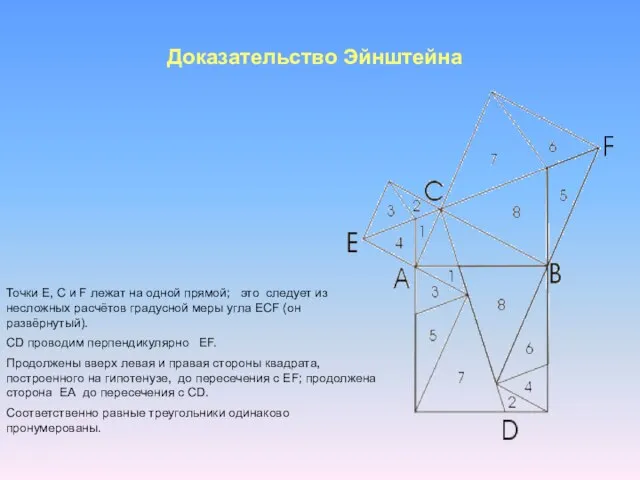
В самом деле, треугольники ABD и BFC равны по двум сторонам и углу между ними: FB = AB, BC = BD, а углы между ними равны как тупые углы со взаимно перпендикулярными сторонами.
SABD = 0,5S BJLD, так как у треугольника ABD и прямоугольника BJLD общее основание BD и общая высота LD. Аналогично SFBC=0,5S ABFH
(BF-общее основание, АВ-общая высота). Отсюда, учитывая, что SABD=SFBC, имеем SBJLD=SABFH.
Аналогично, если вы проведёте отрезок АЕ используете равенство треугольников ВСК и АСЕ, то докажете, что SJCEL=SACKG.
Итак, SABFH+SACKG= SBJLD+SJCEL= SBCED, что и требовалось доказать.
Это доказательство было приведено Евклидом в его "Началах". По свидетельству Прокла (Византия), оно придумано самим Евклидом. Доказательство Евклида приведено в предложении 47 первой книги "Начал".
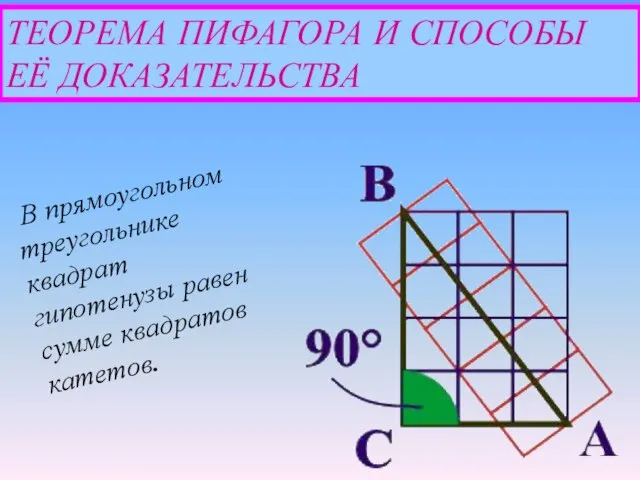
На гипотенузе и катетах прямоугольного треугольника АВС строятся соответствующие квадраты и доказывается, что прямоугольник BJLD равновелик квадрату ABFH, а прямоугольник JCEL - квадрату АGКС. Тогда сумма площадей квадратов на катетах будет равна площади квадрата на гипотенузе.

рис. 2
Древнекитайское доказательство. на древнекитайском чертеже четыре равных прямоугольных треугольника с катетами а, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной а+b, а внутренний — квадрат со стороной с, построенный на гипотенузе (б). Если квадрат со стороной с вырезать и оставшиеся 4 затушеванных треугольника уложить в два прямоугольника (в), то ясно, что образовавшаяся пустота, с одной стороны, равна с2, а с другой — а2+Ь2, т.е. с2=а2+Ь2. Теорема доказана. Заметим, что при таком доказательстве построения внутри квадрата на гипотенузе, которые мы видим на древнекитайском чертеже (а), не используются. По-видимому, древнекитай­ские математики имели другое доказательство. Именно если в квадрате со стороной с два заштрихованных треугольника (б) отрезать и приложить гипотенузами к двум другим гипотенузам (г), то легко обнаружить, что полученная фигура, которую иногда называют «креслом невесты», состоит из двух квадратов со сторонами а и b, т.е. с2=а2+Ь2.

Рис. 4
Древнеиндийское доказательство. Математики Древней Индии заметили, что для доказательства теоремы Пифагора достаточно использовать внутреннюю часть древнекитайского чертежа. В на­писанном на пальмовых листьях трактате «Сиддханта широмани» («Венец знания») крупнейшего индийского математика XII в. Бхаскары помещен чертеж (а) с характерным для индийских доказательств словом «смотри!». Как видим, прямоугольные треугольники уложены здесь гипотенузой наружу и квадрат с2 перекладывается в «кресло невесты» а2-b2 (б). Заметим, что частные случаи теоремы Пифагора (например, построение квадрата, площадь которого вдвое больше площади данного квадрата) встречаются в древнеиндийском трактате «Сульва сутра» (VII —V вв. до н.э.).

Векторное доказательство.
Пусть АВС - прямоугольный треугольник с прямым углом при вершине С, построенный на векторах. Тогда справедливо векторное равенство: b+c=a откуда имеем, что c = a – b. Возводя обе части в квадрат, получим c²=a²+b²-2ab. Так как a перпендикулярно b, то ab=0, откуда c²=a²+b². Нами снова доказана теорема Пифагора.

Область применения.
Теорема Пифагора всегда имела широкое применение при решении самых разнообразных геометрических задач.

Точно неустановленно количество доказательств знаменитой теоремы Пифагора Самосского. Ну приблизительно существует 250-350 доказательств этой теоремы, поэтому она даже попала в Книгу рекордов Гиннеса
А сколько существует доказательств теоремы Пифагора?