Содержание
- 2. Задачи по геометрии в пробных вариантах ЕГЭ
- 3. Задание на дом: Повторить гл.3, определения и формулировки теорем. ЕГЭ 2009, вар.5,В10,В11.
- 4. Проверка домашнего задания.
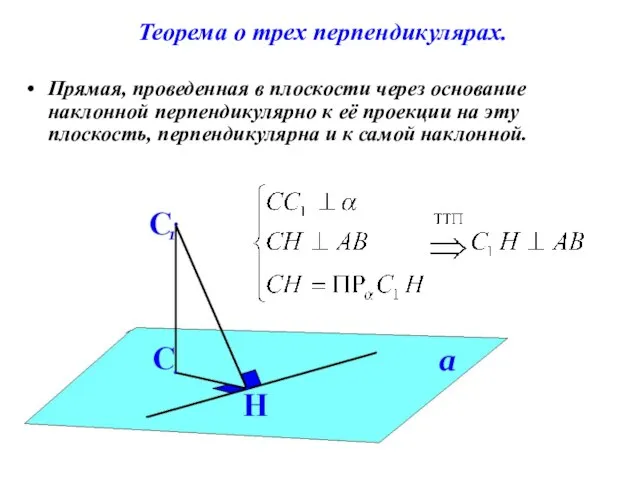
- 5. Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на
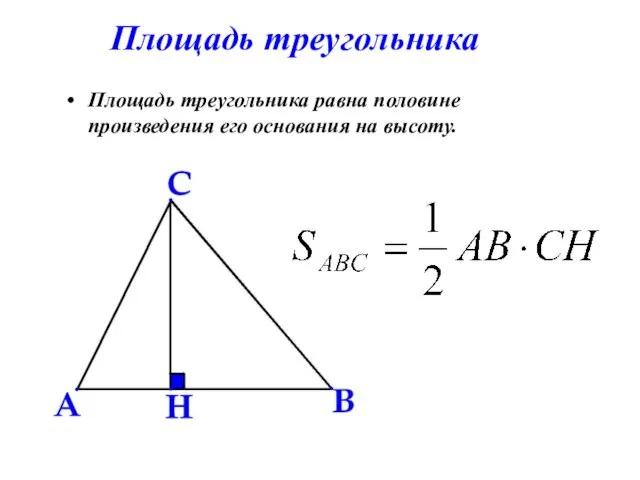
- 6. Площадь треугольника Площадь треугольника равна половине произведения его основания на высоту.
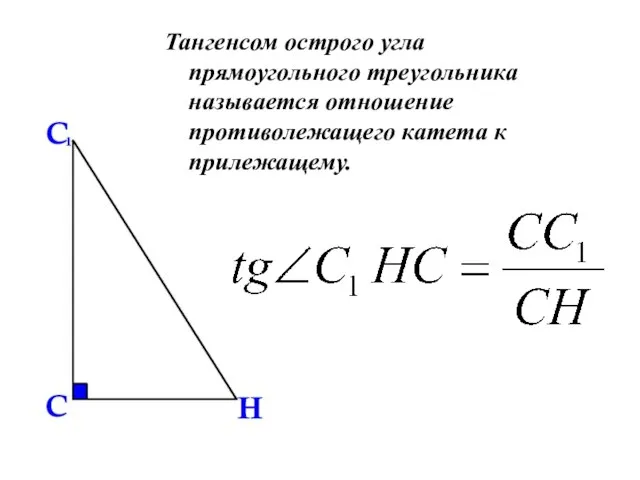
- 7. Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
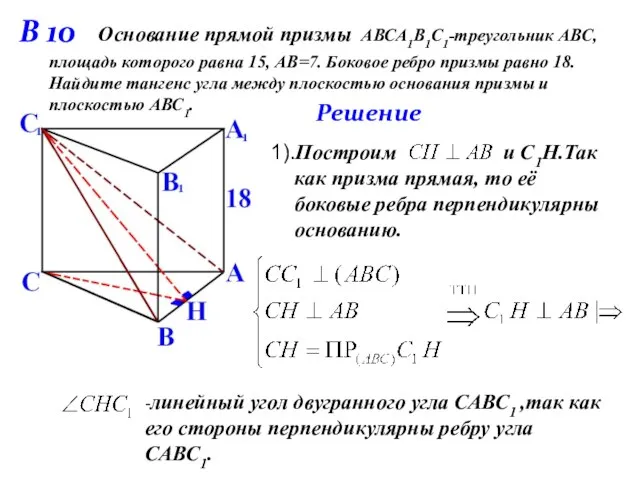
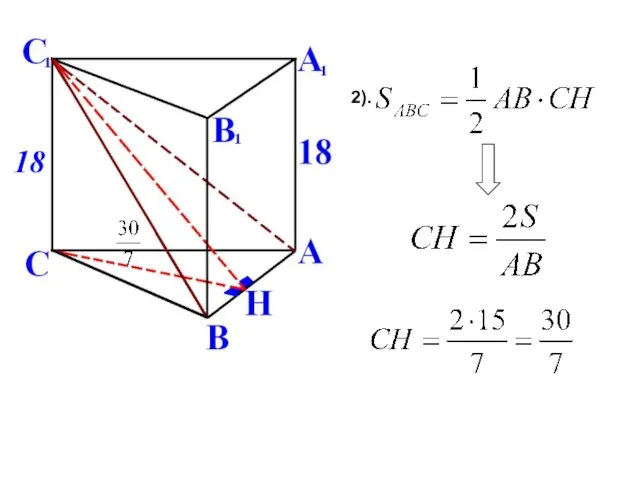
- 8. 1).Построим и С1Н.Так как призма прямая, то её боковые ребра перпендикулярны основанию. Основание прямой призмы АВСА1В1С1-треугольник
- 9. 2). 18
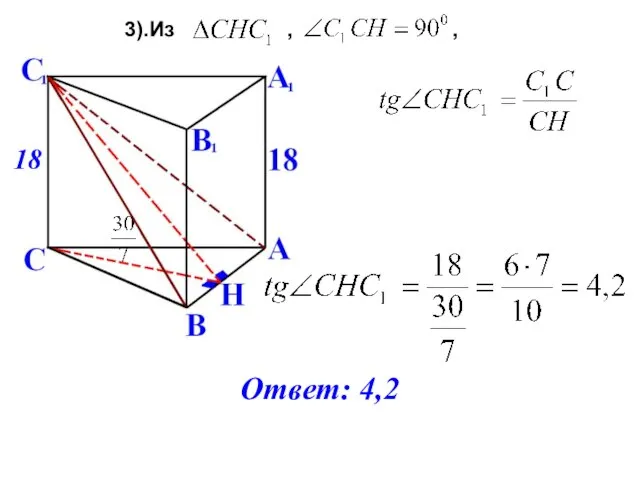
- 10. 3).Из , , 18 Ответ: 4,2
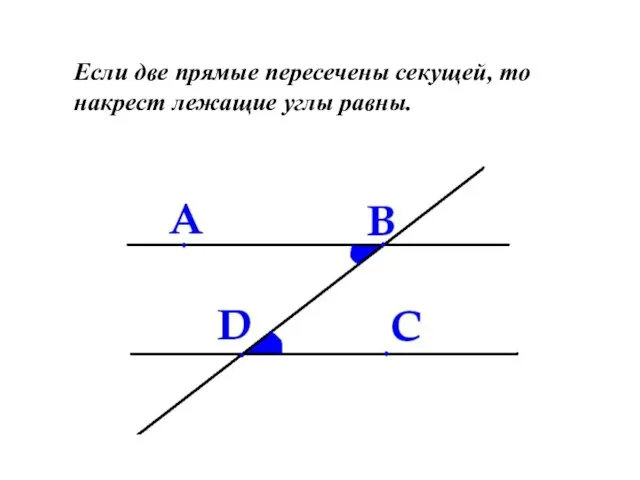
- 11. Если две прямые пересечены секущей, то накрест лежащие углы равны.
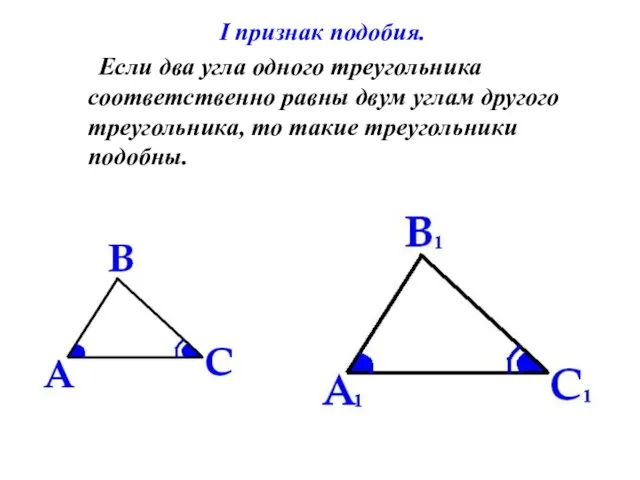
- 12. I признак подобия. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие
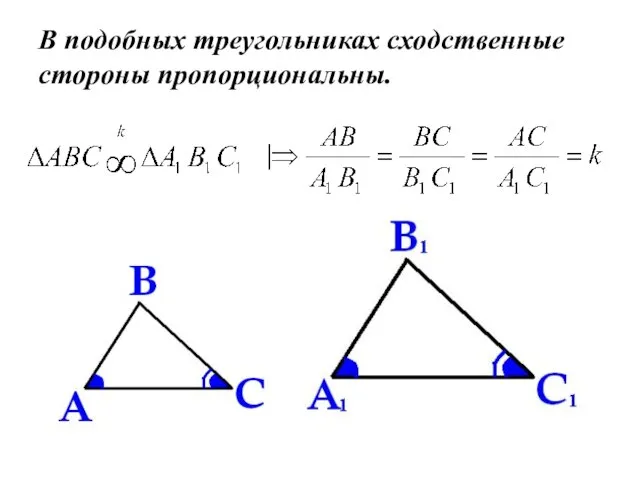
- 13. В подобных треугольниках сходственные стороны пропорциональны.
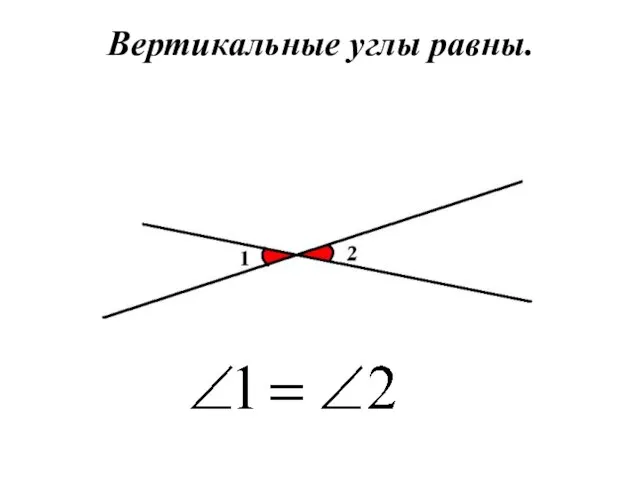
- 14. Вертикальные углы равны.
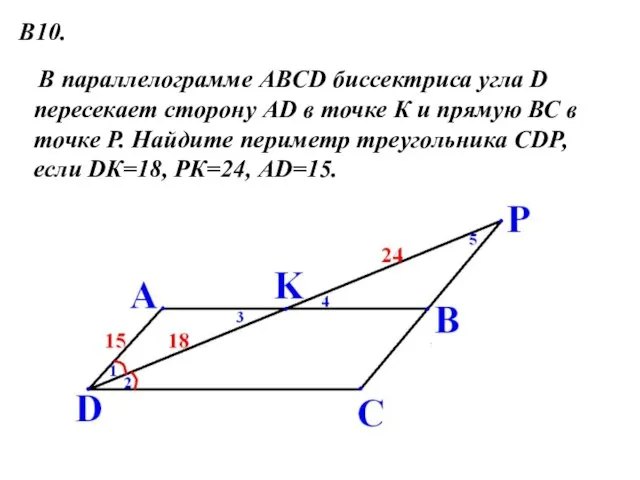
- 15. В параллелограмме АBCD биссектриса угла D пересекает сторону AD в точке К и прямую ВС в
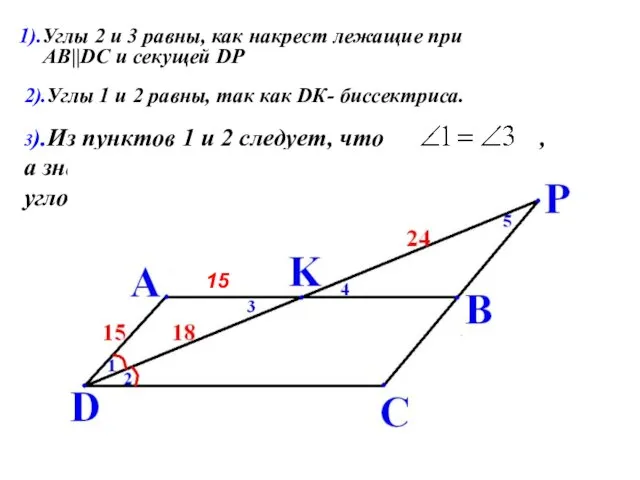
- 16. 3).Из пунктов 1 и 2 следует, что , а значит AD=AK=15, так как напротив равных углов
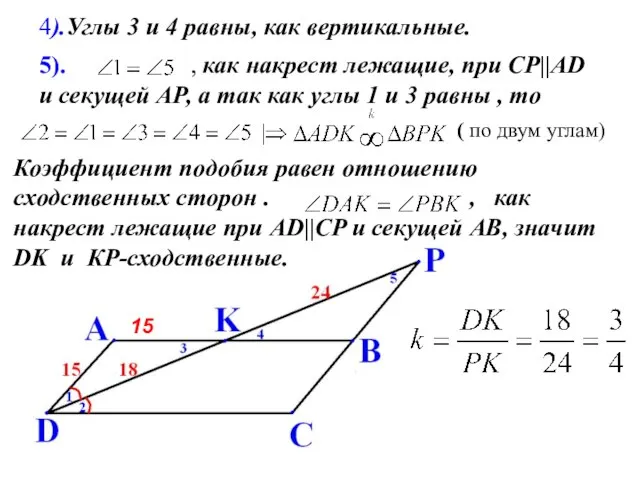
- 17. 5). , как накрест лежащие, при СР||AD и секущей АР, а так как углы 1 и
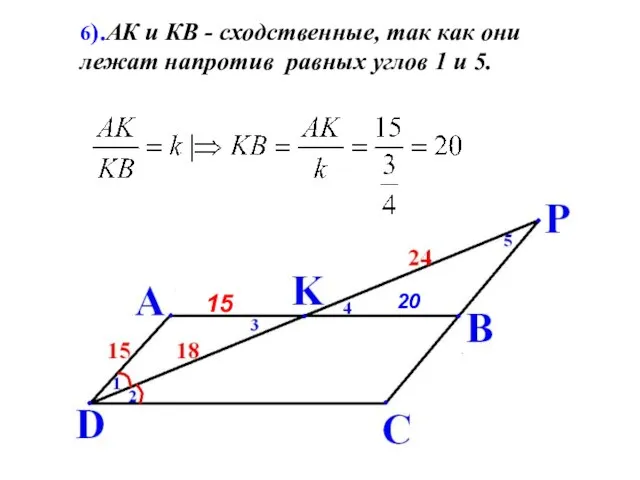
- 18. 6).АК и КВ - сходственные, так как они лежат напротив равных углов 1 и 5. 20
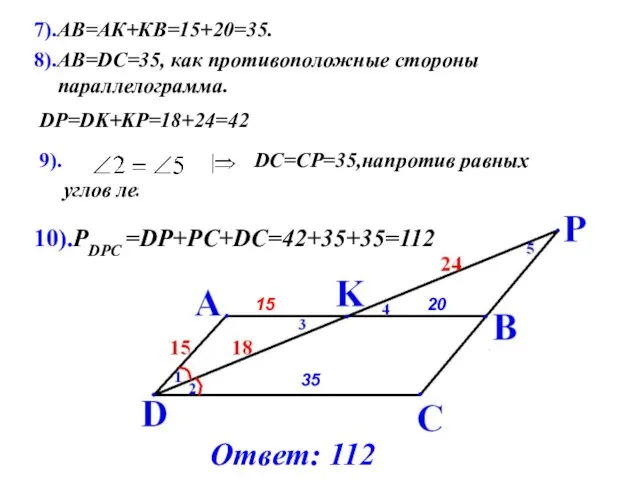
- 19. 9). DC=CP=35,напротив равных углов лежат равные стороны. 15 20 DP=DK+KP=18+24=42 8).АВ=DС=35, как противоположные стороны параллелограмма. 35
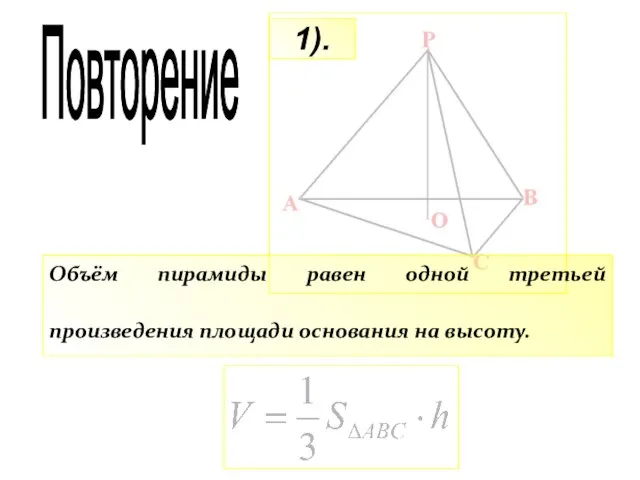
- 20. 1). Объём пирамиды равен одной третьей произведения площади основания на высоту. Повторение
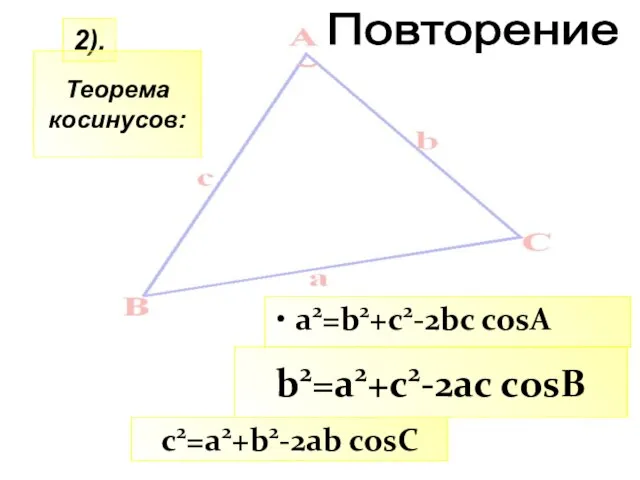
- 21. c2=a2+b2-2ab cosC 2). b2=a2+c2-2ac cosB Повторение a2=b2+c2-2bc cosA Теорема косинусов:
- 22. Теорема Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». c2=a2+b2 3). Повторение
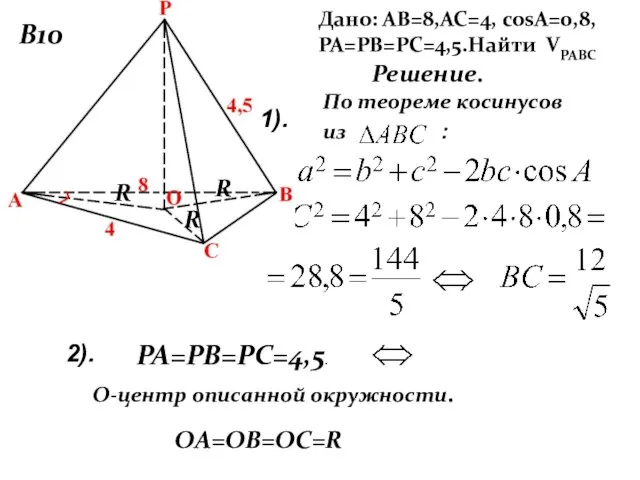
- 23. В10 Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС Решение. По теореме косинусов из : 2). 1). РА=РВ=РС=4,5. OА=OВ=OС=R
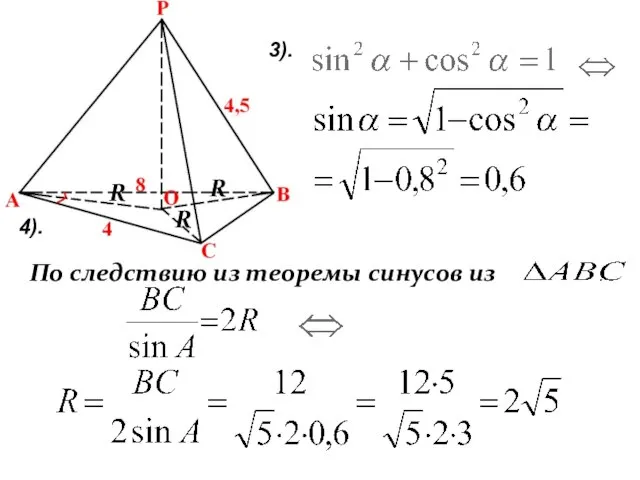
- 24. 4). По следствию из теоремы синусов из : 3). R R R
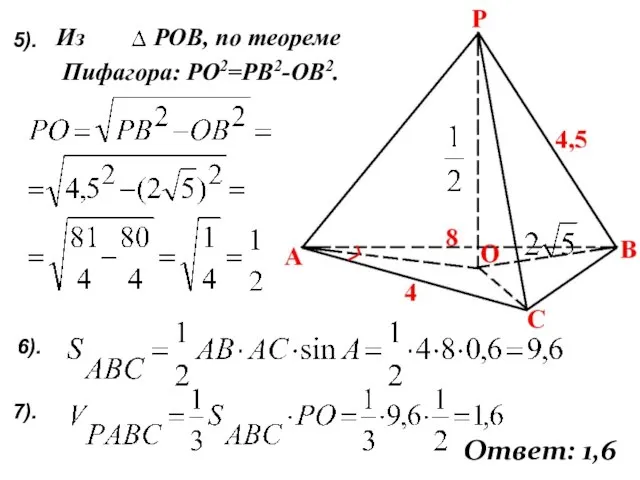
- 25. Из РОВ, по теореме Пифагора: РО2=РВ2-ОВ2. 7). Ответ: 1,6 5). 6).
- 27. Скачать презентацию




 Презентация на тему Опасна ли гроза
Презентация на тему Опасна ли гроза Redaktiruemy_beydzh
Redaktiruemy_beydzh Физкультура. Виды плаванья
Физкультура. Виды плаванья О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС
О некоторых итогах участия МИП СФО в реализации государственных программ Фонда содействия развитию МП в НТС Письмо пером - за и против
Письмо пером - за и против Tin cup design
Tin cup design Транспорт. Виды транспорта
Транспорт. Виды транспорта Новый стандарт: обучаем и учимся
Новый стандарт: обучаем и учимся Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации
Конституционное право. Принцип дисконтинуитета. Перспективы развития в Российской Федерации Виды рабочей одежды
Виды рабочей одежды Я люблю тебя, Сакский район!
Я люблю тебя, Сакский район! Что такое значение?От П.Грайса к теории игр.
Что такое значение?От П.Грайса к теории игр. Тема лекции:«Прикладная информатика в табличном процессоре»
Тема лекции:«Прикладная информатика в табличном процессоре»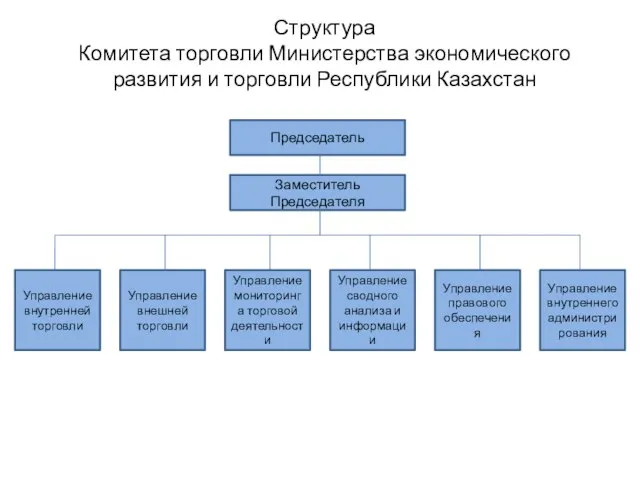 Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан
Структура Комитета торговли Министерства экономического развития и торговли Республики Казахстан Презентация на тему Информация в природе, обществе и технике
Презентация на тему Информация в природе, обществе и технике Основы коммуникативной компетентности педагогов
Основы коммуникативной компетентности педагогов Хочу отдыхать
Хочу отдыхать Урок по рассказам И.А. Бунина о любви
Урок по рассказам И.А. Бунина о любви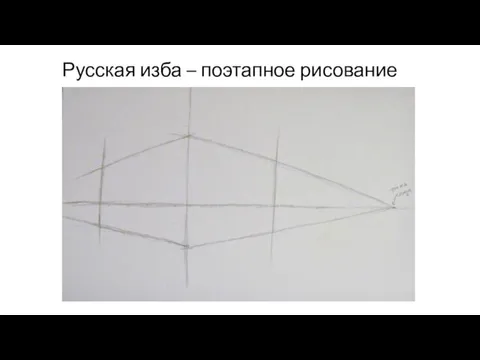 Русская изба – поэтапное рисование
Русская изба – поэтапное рисование Известные люди Австрии
Известные люди Австрии 3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012
3-й КОНКУРСНЫЙ НАБОР ПРОЕКТНЫХ ПРЕДЛОЖЕНИЙПОДГОТОВКА ПРИЛОЖЕНИЯ B: БЮДЖЕТ И ПРИЕМЛЕМОСТЬ РАСХОДОВБеларусь, 30.03.2012 – 05.04.2012 Викторина по произведениям А.П.Чехова « Смешные рассказы»
Викторина по произведениям А.П.Чехова « Смешные рассказы» Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г.
Объединение «Грамматландия» Составила: Мануйлова Н. В. 2011 г. ЮТА (2)
ЮТА (2) Многообразие компьютеров
Многообразие компьютеров Похищение человека
Похищение человека Понятие и особенности административно правовой нормы
Понятие и особенности административно правовой нормы Техника мраморирования в современном дизайне
Техника мраморирования в современном дизайне