Слайд 2Задачи и цели:
Узнать теорию о подобных треугольниках.
Узнать где применяется подобие в жизни.
Рассмотреть

решение задач на местности.
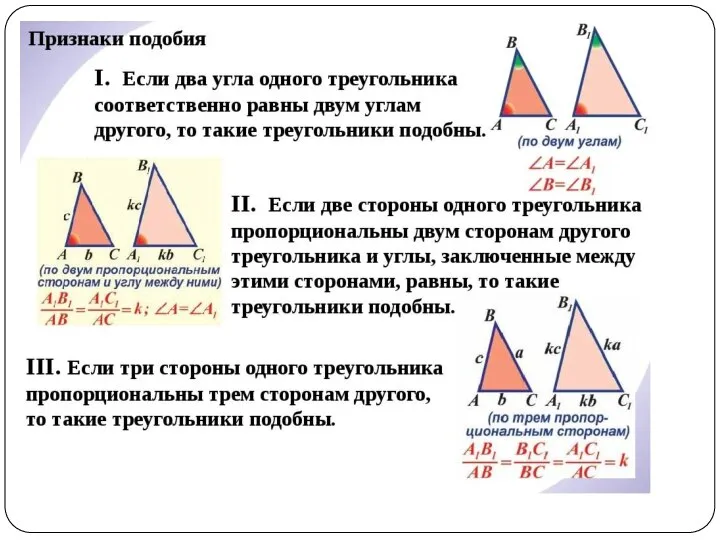
Слайд 3 Теория:
Два треугольника называются подобными, если их углы соответственно равны и стороны
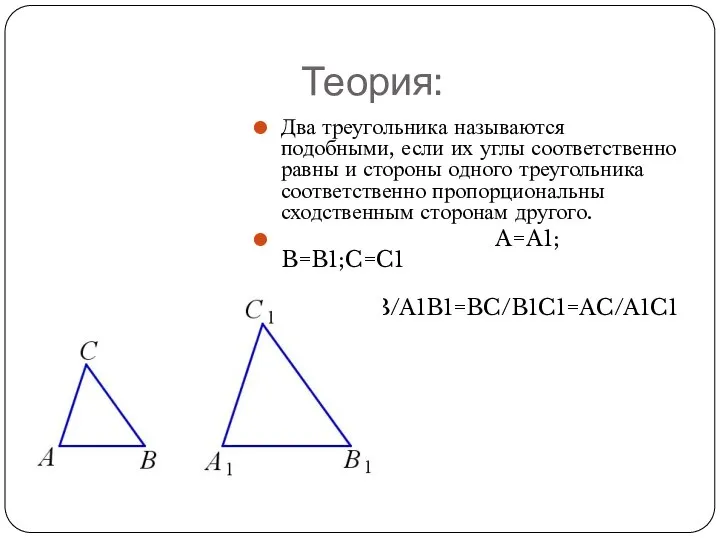
одного треугольника соответственно пропорциональны сходственным сторонам другого.
A=A1; B=B1;C=C1
AB/A1B1=BC/B1C1=AC/A1C1
Слайд 5Образец подзаголовка
Образец заголовка

Слайд 6На следующий день Фалес нашёл длинную палку, воткнул её в землю чуть

поодаль пирамиды. Дождался определённого момента. Провёл некоторые измерения, сказал способ определения высоты пирамиды и назвал её высоту.
Слайд 7 Применение на практике:
Применение теории на практике: Определение высоты предмета По шесту.

Для измерения нужно взять шест, равный по длине вашему росту. Шест этот надо установить на таком расстоянии от дерева, чтобы лежа можно было видеть верхушку дерева на одной прямой линии с верхней точкой шеста. Тогда высота дерева будет равна линии, проведенной от вашей головы до основания дерева.
Слайд 8 Решение задач:
Дано: тр ACD и тр ABE; ED=15;BE=3.
Решение: уг A -
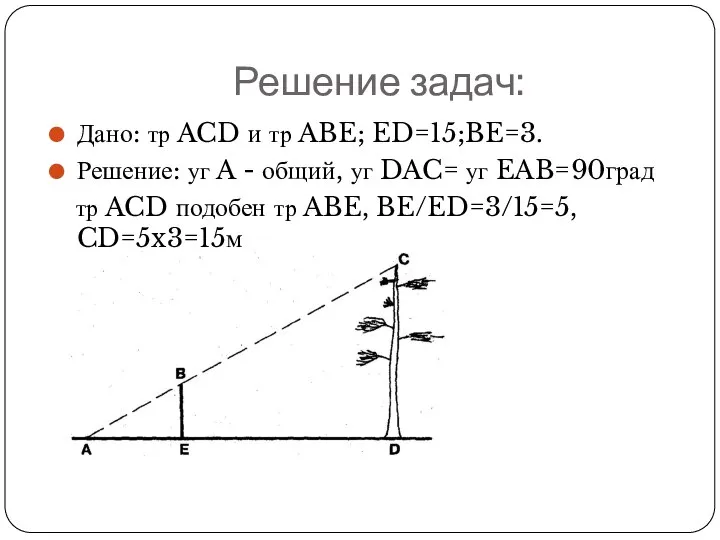
общий, уг DAC= уг EAB=90град
тр ACD подобен тр ABE, BE/ED=3/15=5, CD=5x3=15м
Слайд 9По луже. Этот способ можно удачно применять после дождя, когда на земле
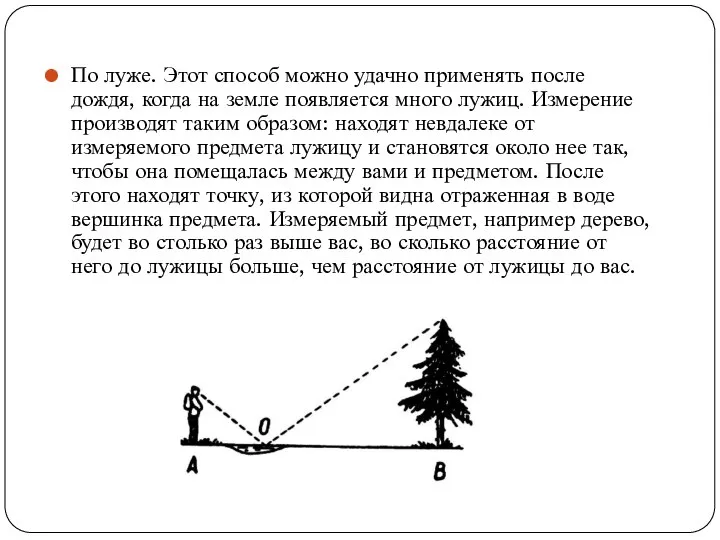
появляется много лужиц. Измерение производят таким образом: находят невдалеке от измеряемого предмета лужицу и становятся около нее так, чтобы она помещалась между вами и предметом. После этого находят точку, из которой видна отраженная в воде вершинка предмета. Измеряемый предмет, например дерево, будет во столько раз выше вас, во сколько расстояние от него до лужицы больше, чем расстояние от лужицы до вас.
Слайд 10 Задача:
По зеркалу: тр АВD подобен тр EFD (по двум углам): уг

ВАD = уг FED=90°; уг АDВ = уг EDF, т.к. угол падения равен углу отражения. В подобных треугольниках сходственные стороны пропорциональны: DE/AD=FE/AB; FE=DSxAB/AD
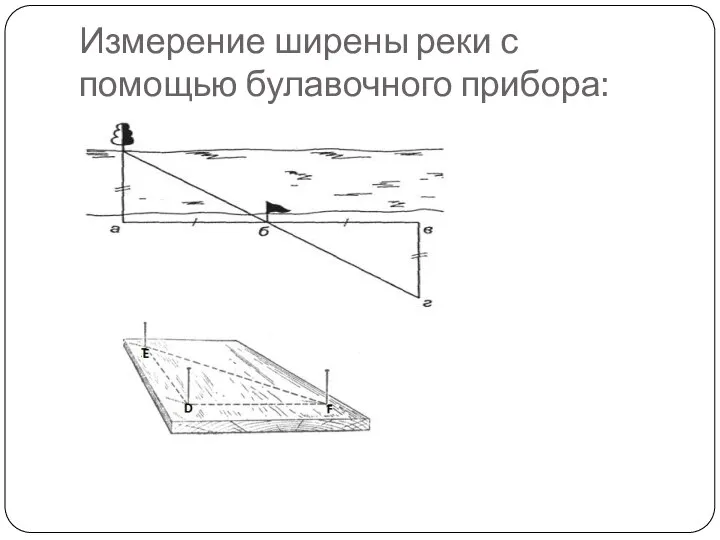
Слайд 11Измерение ширены реки с помощью булавочного прибора:









 ZACT (новая металлизированная упаковка)
ZACT (новая металлизированная упаковка) Акупунктурный электромассажер для ухода за телом Исюэтун
Акупунктурный электромассажер для ухода за телом Исюэтун Викторина «Весенняя капель»
Викторина «Весенняя капель» Ледяное Царство Зона арктических пустынь
Ледяное Царство Зона арктических пустынь С юбилеем Зилара Адисовна
С юбилеем Зилара Адисовна Спелеология
Спелеология Архитектура западноевропейского средневековья
Архитектура западноевропейского средневековья Предпринимательство и бизнес
Предпринимательство и бизнес Золотой ключик или приключения Буратино. Диафильм
Золотой ключик или приключения Буратино. Диафильм Презентация на тему Строчная и заглавная буквы Ц, ц
Презентация на тему Строчная и заглавная буквы Ц, ц Образовательный проект Профильная четверть
Образовательный проект Профильная четверть Презентация на тему Что такое сквернословие и как с ним бороться
Презентация на тему Что такое сквернословие и как с ним бороться Былины
Былины Круглый стол «НАРКОМАНИЯ - ДОБРОВОЛЬНОЕ САМОУБИЙСТВО?» По модулю «Граждановедение» Я.В. Соколова
Круглый стол «НАРКОМАНИЯ - ДОБРОВОЛЬНОЕ САМОУБИЙСТВО?» По модулю «Граждановедение» Я.В. Соколова СИУ
СИУ Доходность акций
Доходность акций Номинация №4«Здоровьесберегающие технологии на уроках МХК»
Номинация №4«Здоровьесберегающие технологии на уроках МХК» Стимуляция роста и контроль заболеваемости растений с помощью универсального биологического средства защиты.
Стимуляция роста и контроль заболеваемости растений с помощью универсального биологического средства защиты. Презентация на тему Ателье по пошиву изделий. Пошив наволочек
Презентация на тему Ателье по пошиву изделий. Пошив наволочек Биссектриса угла
Биссектриса угла Развитие акушерства и гинекологии в России
Развитие акушерства и гинекологии в России Новое поколение тракторов КИРОВЕЦ К-7М
Новое поколение тракторов КИРОВЕЦ К-7М Разнообразие животных
Разнообразие животных Мастерская БольшеЧемЕГЭ. Повышение уровня сдачи ВПР, ОГЭ, ЕГЭ
Мастерская БольшеЧемЕГЭ. Повышение уровня сдачи ВПР, ОГЭ, ЕГЭ Встреча кандидата с населением
Встреча кандидата с населением Презентация на тему Религия
Презентация на тему Религия Национальные Парки США и Великобритании
Национальные Парки США и Великобритании Предложения ARQA Technologies для брокеров Владимир Курляндчик Директор по развитию, ARQA Technologies
Предложения ARQA Technologies для брокеров Владимир Курляндчик Директор по развитию, ARQA Technologies