Содержание
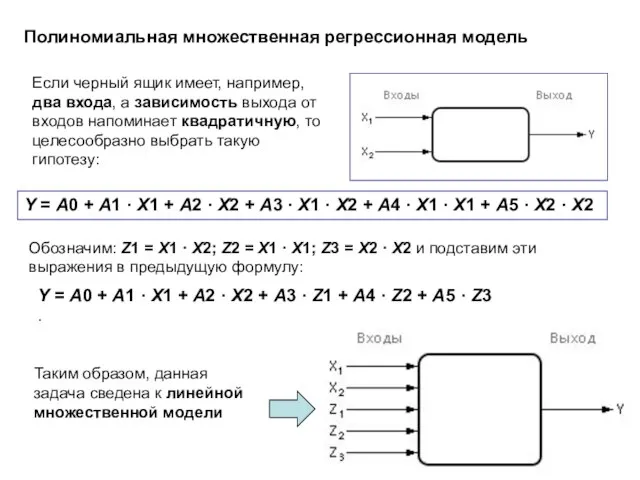
- 2. Полиномиальная множественная регрессионная модель Если черный ящик имеет, например, два входа, а зависимость выхода от входов
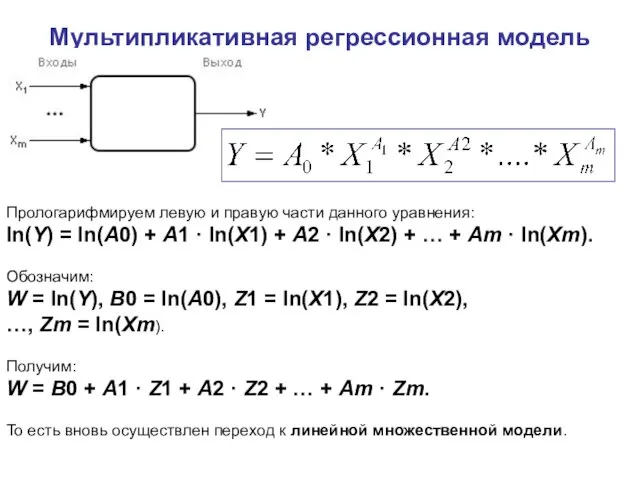
- 3. Мультипликативная регрессионная модель Прологарифмируем левую и правую части данного уравнения: ln(Y) = ln(A0) + A1 ·
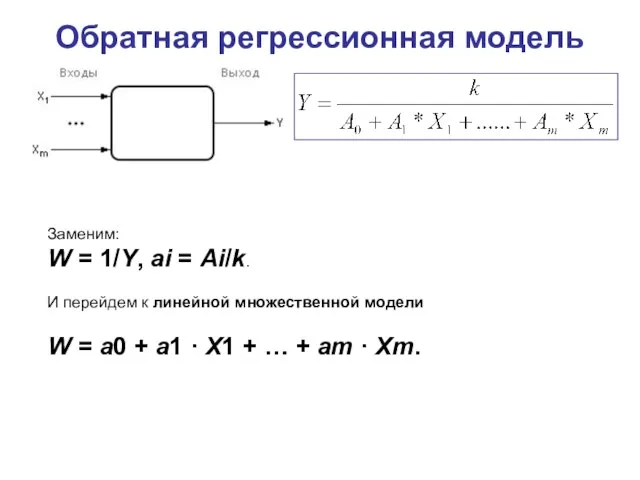
- 4. Обратная регрессионная модель Заменим: W = 1/Y, ai = Ai/k. И перейдем к линейной множественной модели
- 5. Экспоненциальная модель Прологарифмируем левую и правую части уравнения: ln(Y) = B0 + B1 · X1 +
- 6. Регрессионный анализ нелинейной модели Получены экспериментальные данные: По виду график похож на степенную функцию Для нахождения
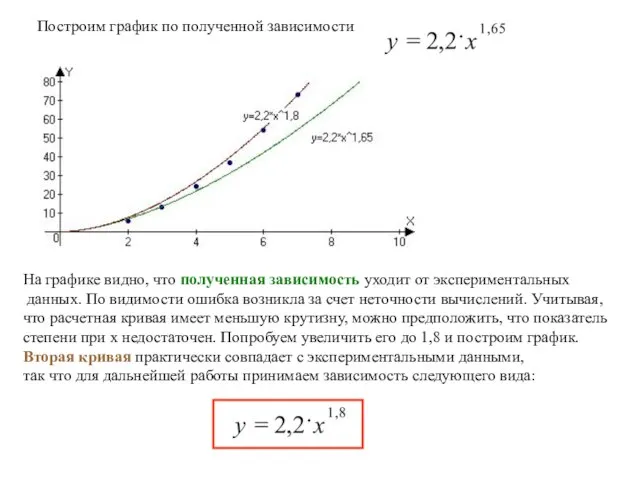
- 7. Построим график по полученной зависимости На графике видно, что полученная зависимость уходит от экспериментальных данных. По
- 9. Скачать презентацию


 Сердечная недостаточность
Сердечная недостаточность Проектирование котельных, ИТП, АИТП
Проектирование котельных, ИТП, АИТП Управление финансовыми рисками
Управление финансовыми рисками Орифлэйм Скин Эксперт
Орифлэйм Скин Эксперт Всегда носите своё детство с собой, и вы никогда не состаритесь
Всегда носите своё детство с собой, и вы никогда не состаритесь Лекция19
Лекция19 Интернет полезен!
Интернет полезен! Правописание суффиксов глаголов –ова-(-ева-), -ыва-(-ива-)
Правописание суффиксов глаголов –ова-(-ева-), -ыва-(-ива-) ГЕСТОЗ: современные представления об этиопатогенезе, диагностике, лечении
ГЕСТОЗ: современные представления об этиопатогенезе, диагностике, лечении Презентация к занятию на тему Денежные средства и их использование
Презентация к занятию на тему Денежные средства и их использование Разработка проекта по применению концепции современного использования оборудования и общего производительного обслуживания обо
Разработка проекта по применению концепции современного использования оборудования и общего производительного обслуживания обо Юные туристы
Юные туристы Презентация на тему Насекомые и пауки.
Презентация на тему Насекомые и пауки.  Волейбол для начинающих
Волейбол для начинающих Superstions in Russia and Britain
Superstions in Russia and Britain Максимилиан Волошин «Гражданская война»
Максимилиан Волошин «Гражданская война» Система оценки достижения планируемых результатов освоения основной образовательной программы
Система оценки достижения планируемых результатов освоения основной образовательной программы Выставка творческих работ. Дорога и мы
Выставка творческих работ. Дорога и мы артикуляционная гимнастика
артикуляционная гимнастика Певчий дрозд
Певчий дрозд Изменения, связанные с запуском рынка мощности. Презентация для потребителей.
Изменения, связанные с запуском рынка мощности. Презентация для потребителей. НАШИ DОСТИЖЖЕНИЯ
НАШИ DОСТИЖЖЕНИЯ Разработка и продвижение капсульной коллекции ФК Зенит
Разработка и продвижение капсульной коллекции ФК Зенит Direct Mail
Direct Mail Новгородская земля
Новгородская земля 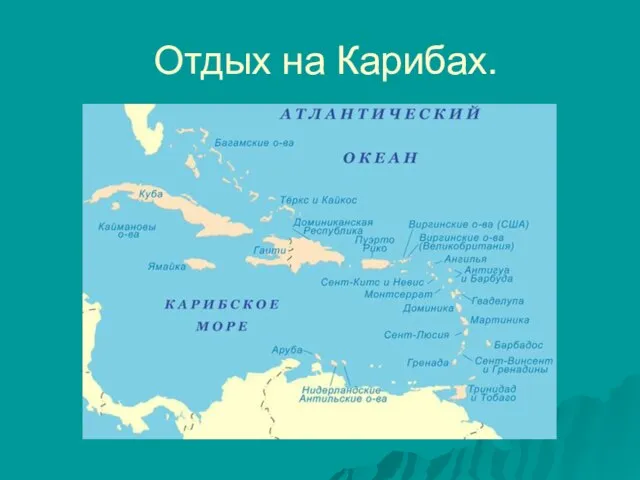 Отдых на Карибах.
Отдых на Карибах. Басни крылова
Басни крылова Техника безопасности Шашмыркина и Жернакова
Техника безопасности Шашмыркина и Жернакова