Понятие потенциала, потенциальный характер политического поля

4.1. Вывод формулы для расчета работы сил поля при перемещении зарядов.
4.2. Понятие потенциала, потенциальный характер электростатического поля.
4.3. Связь между напряженностью и потенциалом.
4.4. Потенциал поля плоского конденсатора, заряженной нити, цилиндрического и сферического конденсаторов.
ОГЛАВЛЕНИЕ

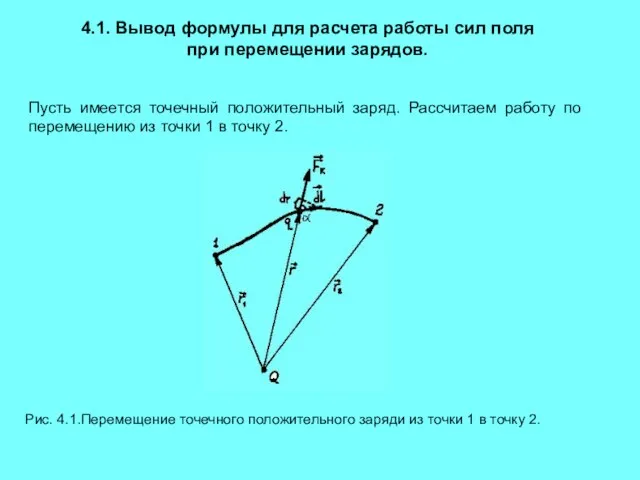
Пусть имеется точечный положительный заряд. Рассчитаем работу по перемещению из точки 1 в точку 2.
4.1. Вывод формулы для расчета работы сил поля при перемещении зарядов.
Рис. 4.1.Перемещение точечного положительного заряди из точки 1 в точку 2.

Вывод: работа по перемещению заряда из одной точки поля в другую равна произведению величины этого заряда на разность потенциалов начальной и конечной точек траектории.
К оглавлению
(4.1)

4.2. Понятие потенциала, потенциальный характер электростатического поля.
может служить характеристикой поля.
Т. к. при
функциональная часть выражения (4.2)
const = 0. Получим
, то примем
Эта величина получила название потенциал поля точечного заряда.
(4.2)
(4.3)
(4.4)
(4.5)

Потенциалом поля в данной точке называется физическая величина, численно равная работе по переносу единичного положительного заряда из данной точки поля в бесконечность.
Работа сил электростатического поля равна убыли потенциальной энергии, т. е.
Тогда, сравнив (4.4) и (4.6), получим
Т. к. при
, то
Потенциалом поля в данной точке называется физическая величина, численно равная потенциальной энергии, которая приобретается единичным положительным зарядом при переносе из бесконечности в данную точку поля.
Выясним свойства потенциального электростатического поля.
Рис. 4.2.
(4.6)
(4.7)
(4.8)
(4.9)

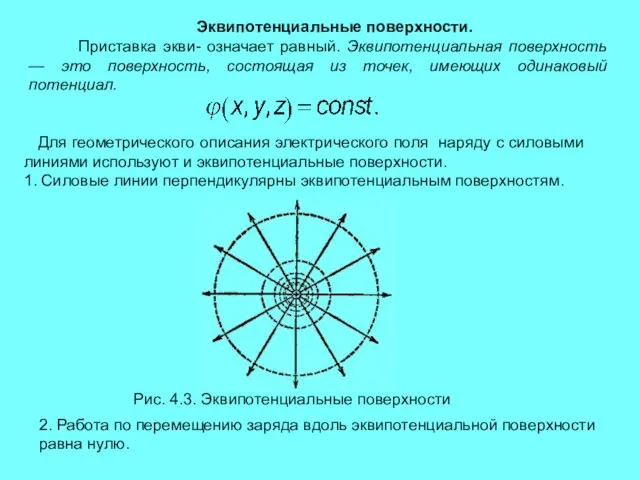
1. Работа по переносу из одной точки электрического поля в другую не зависит от формы траектории.
2. Работа по переносу заряда вдоль замкнутого пути равна нулю. 1 и 2 отражают потенциальный характер поля.
3. В электрическом поле циркуляция вектора напряженности вдоль замкнутого контура равна нулю.
(4.10)

Эквипотенциальные поверхности.
Приставка экви- означает равный. Эквипотенциальная поверхность — это поверхность, состоящая из точек, имеющих одинаковый потенциал.
Для геометрического описания электрического поля наряду с силовыми линиями используют и эквипотенциальные поверхности.
1. Силовые линии перпендикулярны эквипотенциальным поверхностям.
2. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Рис. 4.3. Эквипотенциальные поверхности

Опыт 4.1. Демонстрация эквипотенциальных поверхностей.
Цель:
Демонстрация эквипотенциальных поверхностей.
Оборудование:
Электрометр демонстрационный.
Конусообразный кондуктор на изолирующем штативе.
Эбонитовая палочка.
Шерсть.
Шарик пробный на изолирующей ручке.
Два проводника: один – длиной 1,5 - 2 м гибкий, другой – для заземления электрометра.
Рис. 4.4.Установка
Выводы: поверхность заряженного проводника всюду имеет одинаковый потенциал.
К оглавлению
Ход работы:
Пробный шарик с длинным проводником соединён со стержнем электроскопа, корпус заземлён. Заряжаем кондуктор и шарик перемещаем по всей поверхности (наружной и внутренней) кондуктора. Показания электрометра не меняются.

4.3. Связь между напряженностью и потенциалом.
Пусть имеется векторное поле
и некоторое скалярное
поле
Известно, что между напряженностью и потенциалом электростатического поля существует связь:
К оглавлению
(4.11)
(4.12)

4.4. Потенциал поля плоского конденсатора, заряженной нити, цилиндрического и сферического конденсаторов.
Однородный плоский конденсатор.
Рис. 4.4. Однородный плоский конденсатор
Задание для самостоятельной работы.
Используя материал лекций 3 и 4 вывести формулы, описывающие потенциал поля заряженной нити, цилиндрического и сферического конденсаторов.
К оглавлению
(4.13)

мы знаем что
найдем разность потенциалов между обкладками конденсатора путем интегрирования
Если зазор между обкладками относительный, т.е. выполняется условие
в этом случае
Для цилиндрического конденсатора
Рис.4.5