Содержание
- 2. 3.1. Основные определения. 3.2. Теорема Остроградского – Гаусса для дискретного и непрерывного распределения зарядов. 3.3. Применение
- 3. если 3.1. Основные определения 1. Линейная плотность заряда — это физическая величина, численно равная заряду, приходящемуся
- 4. . 2. Поверхностная плотность заряда – это физическая величина, численно равная заряду, приходящемуся на единицу площади.
- 5. 3. Объемная плотность заряда ρ – это физическая величина, численно равная заряду, заключенному в единице объема
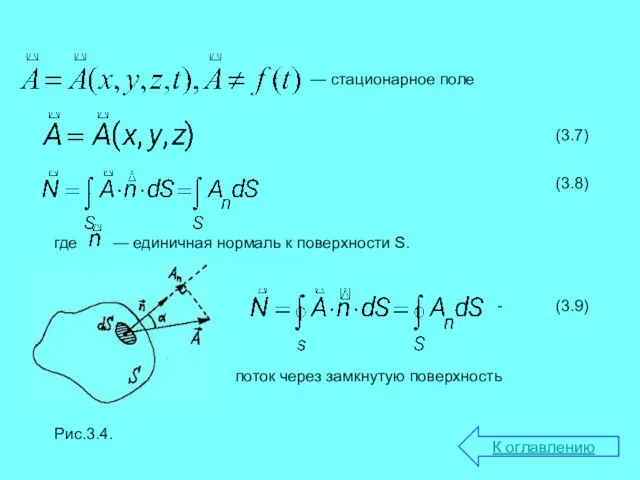
- 6. — стационарное поле поток через замкнутую поверхность К оглавлению где — единичная нормаль к поверхности S.
- 7. 3.2. Теорема Остроградского-Гаусса Пусть имеется уединенный точечный заряд. Рассчитаем поток вектора этого заряда через замкнутую поверхность,
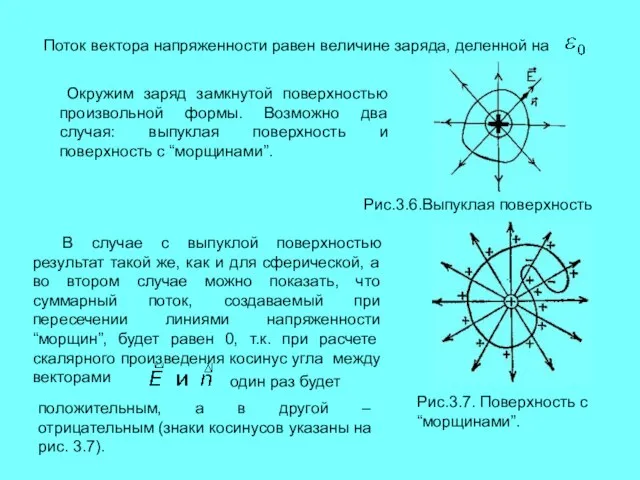
- 8. . Поток вектора напряженности равен величине заряда, деленной на Окружим заряд замкнутой поверхностью произвольной формы. Возможно
- 9. Поэтому можно сказать, что поток вектора напряженности поля точечного заряда через произвольно замкнутую поверхность, окружающую этот
- 10. . В случаях, если имеется непрерывное распределение зарядов в некоторых телах, необходимо от операции суммирования перейти
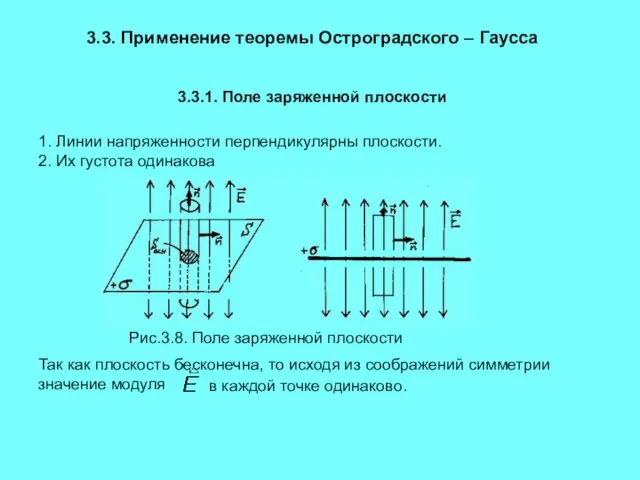
- 11. 3.3. Применение теоремы Остроградского – Гаусса 3.3.1. Поле заряженной плоскости 1. Линии напряженности перпендикулярны плоскости. 2.
- 12. т.к. проекция вектора на нормаль к боковой поверхности равна нулю, то К оглавлению (3.14)
- 13. 3.3.2. Поле разноименных плоскостей Применим принцип суперпозиции: К оглавлению Рис.3.9. Поле разноименных плоскостей Рис.3.10. (3.15)
- 14. 3.3.3. Поле заряженной нити. К оглавлению Рис.3.11. Поле заряженной нити (3.16)
- 15. 3.3.4. Поле заряженной сферы. Поле внутри сферы. Рис.3.12. Поле внутри сферы. (3.17)
- 16. Поле вне сферы Т. к. , то Если К оглавлению Рис.3.13. Поле вне сферы (3.18) (3.19)
- 17. 3.3.5. Поле заряженного шара Поле внутри шара. Рис.3.14. Поле внутри шара. (3.21)
- 18. Поле вне шара. - обратно квадратичная зависимость. К оглавлению Рис.3.15. Поле вне шара (3.22)
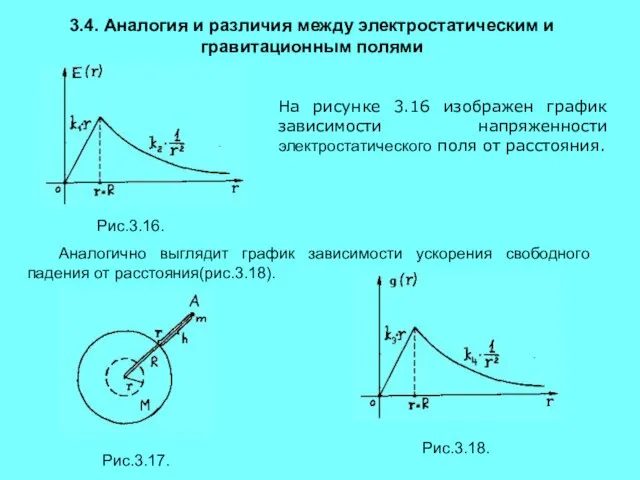
- 19. 3.4. Аналогия и различия между электростатическим и гравитационным полями Аналогично выглядит график зависимости ускорения свободного падения
- 21. Скачать презентацию














 Законодательство Республики Казахстан в области информационной безопасности
Законодательство Республики Казахстан в области информационной безопасности Духи
Духи Обобщение темы«Тепловые явления»
Обобщение темы«Тепловые явления» Каникулы
Каникулы Родительское собрание
Родительское собрание П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны
П рофильное обучение в старших классах, ориентированно на индивидуализацию обучения и социализацию обучающихся (с учетом реальны Зима в парке
Зима в парке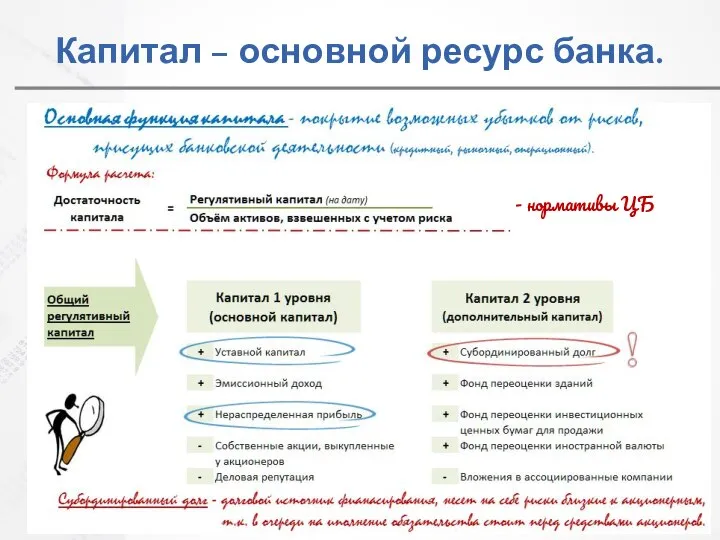 Капитал - основной ресурс банка. Формулы
Капитал - основной ресурс банка. Формулы Hyundai Sonata2.7V6сравнение с конкурентами
Hyundai Sonata2.7V6сравнение с конкурентами Кристаллические тела 10 класс
Кристаллические тела 10 класс Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют
Глава №9. Международные сопоставления ВВП и его компонентов на основе паритетов покупательской способности валют Презентация на тему Каменный уголь
Презентация на тему Каменный уголь  РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК
РАЗВИТИЕ ТЕХНОЛОГИЙ ПРОВЕДЕНИЯ МЕЖРЕГИОНАЛЬНЫХ СДЕЛОК Выколотка. Чеканка. Гравировка
Выколотка. Чеканка. Гравировка Презентация на тему «История создания Linux»
Презентация на тему «История создания Linux» Презентация на тему Лес наш друг
Презентация на тему Лес наш друг  Презентация на тему Русско-японская война 1904-1905 гг
Презентация на тему Русско-японская война 1904-1905 гг  Презентация на тему Английские колонии в Северной Америке 7 класс
Презентация на тему Английские колонии в Северной Америке 7 класс Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул
Мãн Хураçкари пĕтемĕшле пĕлӳ паракан тĕп шкул Презентация на тему Famous British Writers (Знаменитые британские писатели)
Презентация на тему Famous British Writers (Знаменитые британские писатели)  ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI
ЗАБЕЗПЕЧЕННЯ ДОСТУПУ ДО ПУБЛІЧНОI ІНФОРМАЦІI Црква у хришћанској архитектури
Црква у хришћанској архитектури Природные зоны. Лес. Растения леса
Природные зоны. Лес. Растения леса Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы
Краткое описание ресурса Одни из немногих футбольных интернет ресурсов на территории Украины, который подает информацию на 2-х язы My favourite city. Шаблон
My favourite city. Шаблон Презентация на тему Литература Древней Руси
Презентация на тему Литература Древней Руси urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7
urok-povtoreniya-po-kursu-obschestvoznaniya-dlya-7 Современное искусство Египта
Современное искусство Египта