Содержание
- 2. ПОВТОРЕНИЕ
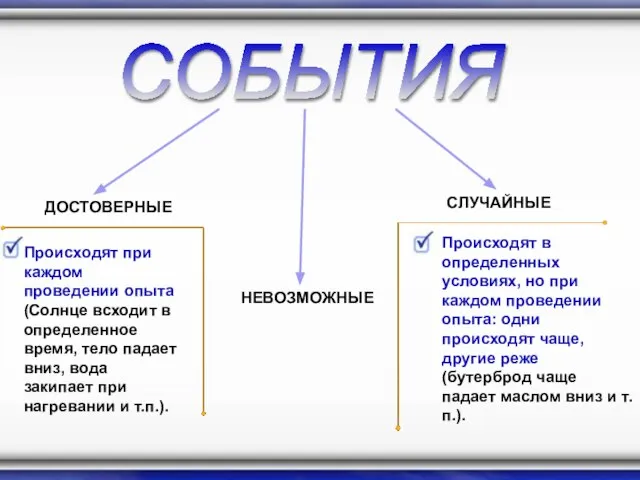
- 3. СОБЫТИЯ ДОСТОВЕРНЫЕ СЛУЧАЙНЫЕ Происходят при каждом проведении опыта (Солнце всходит в определенное время, тело падает вниз,
- 4. ТЕСТ «Случайные исходы, события, испытания».
- 5. 1. О каком событии идёт речь? «Из 25 учащихся класса двое справляют день рождения 30 февраля».
- 6. 2. Это событие является случайным: А) слово начинается с буквы«ь»; В) ученику 9 класса 14 месяцев;
- 7. 3. Найдите достоверное событие: А) На уроке математики ученики делали физические упражнения; В) Сборная России по
- 8. 4. Среди пар событий, найдите несовместимые. А) В сыгранной Катей и Славой партии шахмат, Катя проиграла
- 9. 5.Охарактеризуйте случайное событие: «новая электролампа не загорится». Это событие: А) менее вероятно ; В) равновероятное ;
- 10. 6. Какие события из перечисленных ниже являются противоположными? В колоде карт лежат четыре туза и четыре
- 11. 7. Колобок катится по лесным тропкам куда глаза глядят. На полянке его тропинка расходится на четыре
- 12. 8. Два стрелка делают по одному выстрелу в мишень. Сколько исходов двух совместных выстрелов? А) 4;
- 13. 9. Два шахматиста играют подряд две партии. Сколько исходов у этого события? А) 4; В) 2;
- 14. 10*. Случайный опыт состоит в выяснении пола детей в семьях с тремя детьми. Сколько возможных исходов
- 15. ПОНЯТИЕ ВЕРОЯТНОСТИ
- 16. В толковом словаре С.И. Ожегова и Н.Ю. Шведовой: «Вероятность – возможность исполнения, осуществимости чего-нибудь». Основатель современной
- 17. Известно, по крайней мере, шесть основных схем определения и понимания вероятности. Не все они в равной
- 18. КЛАССИЧЕСКОЕ СТАТИСТИЧЕСКОЕ ГЕОМЕТРИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 19. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
- 20. ВЕРОЯТНОСТЬ – ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ. ТЕОРИЯ ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО
- 21. Вероятностью Р наступления случайного события А называется отношение , где n – число всех возможных исходов
- 22. Пьер-Симо́н Лапла́с Классическое определение вероятности было впервые дано в работах французского математика Лапласа.
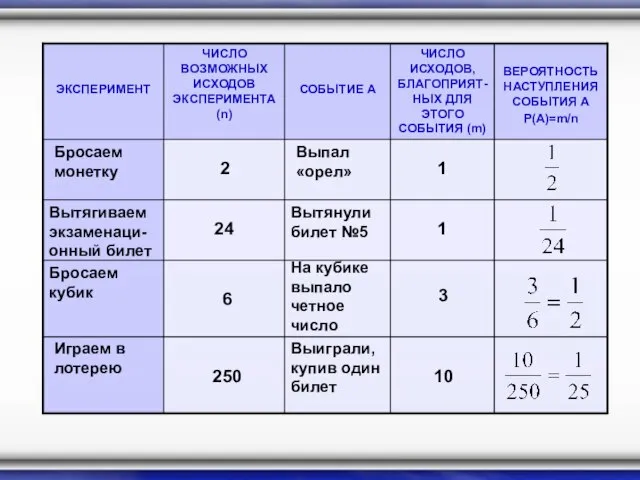
- 23. Бросаем монетку 2 Выпал «орел» 1 Вытягиваем экзаменаци- онный билет Вытянули билет №5 24 1 Бросаем
- 24. Пример 1 В школе 1300 человек, из них 5 человек хулиганы. Какова вероятность того, что один
- 25. Вероятность: P(A) = 5/1300 = 1/250. Решение
- 26. Пример 2. При игре в нарды бросают 2 игральных кубика. Какова вероятность того, что на обоих
- 27. Решение Составим следующую таблицу Вероятность: P(A)=6/36= =1/6.
- 28. Пример 3. Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить? Какие события
- 29. Всего 10 букв. Буква «с» встречается 2 раза – P(с) = 2/10 = 1/5; буква «т»
- 30. Свойства вероятности
- 31. Вероятность достоверного события равна Вероятность невозможного события равна Вероятность события А не меньше , но не
- 32. P(u) = 1 (u – достоверное событие); P(v) = 0 (v – невозможное событие); 0 ≤
- 33. Самостоятельная работа
- 34. Задача 1. В коробке 4 синих, 3 белых и 2 желтых фишки. Они тщательно перемешиваются, и
- 35. а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна: P=3:9=1/3=0,33(3) б) Мы имеем всевозможных
- 36. Задача 2. В коробке лежат 10 одинаковых шаров, на каждом из которых написан его номер от
- 37. Всевозможных событий 6 (красный №1 - красный №2; красный №1 - белый; красный №2 - белый;
- 38. Задача 3. Мальчики играли в “Орлянку”. Но монетка куда-то закатилась. Предложите, как заменить ее игральным кубиком?
- 39. Считать "орел" - четное число, а "решка" - не четное число. Считать "орел" - четное число,
- 40. Задача 4. Какую справедливую игру можно предложить двум девочкам, у которых есть 3 красных и 1
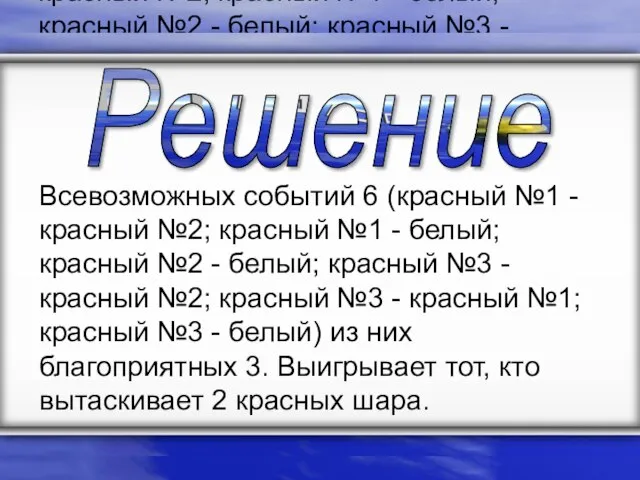
- 41. Всевозможных событий 6 (красный №1 - красный №2; красный №1 - белый; красный №2 - белый;
- 42. Задача 5. В настольной игре сломалась вертушка с тремя разными секторами: красным, белым и синим, но
- 43. Считать на кубике 1 и 2 - красный сектор, 3 и 4 - синий сектор, 5
- 44. Домашнее задание
- 46. Скачать презентацию







































 webp
webp Пьеса На Дне
Пьеса На Дне Моя история tatto
Моя история tatto Безударная гласная
Безударная гласная Классицизм в архитектуре, искусстве, литературе, музыке
Классицизм в архитектуре, искусстве, литературе, музыке Роль налогов в жизни людей
Роль налогов в жизни людей Контроль качества уборки номеров в гостинице
Контроль качества уборки номеров в гостинице Peter Piper
Peter Piper «Общественное движение людей с инвалидностью как фактор модификации публичной сферы (на примере социокультурных проектов РООИ «
«Общественное движение людей с инвалидностью как фактор модификации публичной сферы (на примере социокультурных проектов РООИ « Профессиональные стандарты педагогических работников: изменения и нововведения
Профессиональные стандарты педагогических работников: изменения и нововведения Биосфера — живая оболочка Земли
Биосфера — живая оболочка Земли Tribes and small nations
Tribes and small nations OKiR_Lektsia_5
OKiR_Lektsia_5 Презентация на тему День космонавтики 12 апреля
Презентация на тему День космонавтики 12 апреля Классификация способов сварки давлением
Классификация способов сварки давлением ЭЛЕКТРОННАЯ ШКОЛА
ЭЛЕКТРОННАЯ ШКОЛА Презентация на тему Планирование классного руководителя
Презентация на тему Планирование классного руководителя Служба войск и ее задачи
Служба войск и ее задачи НОУ Школа карвинга
НОУ Школа карвинга Презентация на тему УПРАВЛЕНИЕ ТАМОЖЕННЫМ ДЕЛОМ В ТАМОЖЕННОМ СОЮЗЕ: ТЕОРЕТИКО-ПРАВОВОЙ АСПЕКТ
Презентация на тему УПРАВЛЕНИЕ ТАМОЖЕННЫМ ДЕЛОМ В ТАМОЖЕННОМ СОЮЗЕ: ТЕОРЕТИКО-ПРАВОВОЙ АСПЕКТ  Product placement в кинематографе
Product placement в кинематографе Сделки в гражданском праве
Сделки в гражданском праве Поля листа
Поля листа The museum. Информация о студии
The museum. Информация о студии Кальцимилк молочные конфеты, обогащенные кальцием, магнием, витаминами С и D 3.
Кальцимилк молочные конфеты, обогащенные кальцием, магнием, витаминами С и D 3. Мораль как форма общественного сознания Подготовила: Студентка группы Т-114с Климушина Юлия
Мораль как форма общественного сознания Подготовила: Студентка группы Т-114с Климушина Юлия Лыжные гонки. Зимние виды спорта
Лыжные гонки. Зимние виды спорта Падежи имени существительного
Падежи имени существительного