Содержание
- 2. i = Im sin(ωt+ψi) – мгновенный ток последовательной цепи Мгновенные напряжения на элементах: 1) на резисторе
- 3. 2) на индуктивности L uL = xLIm sin(ωt+ψi+900) = UmLsin(ωt+ψi+900) – на индуктивности напряжение опережает ток
- 4. 3) на конденсаторе (емкости) С uС = xСIm sin(ωt+ψi-900) = UmСsin(ωt+ψi-900) – на емкости (конденсаторе) напряжение
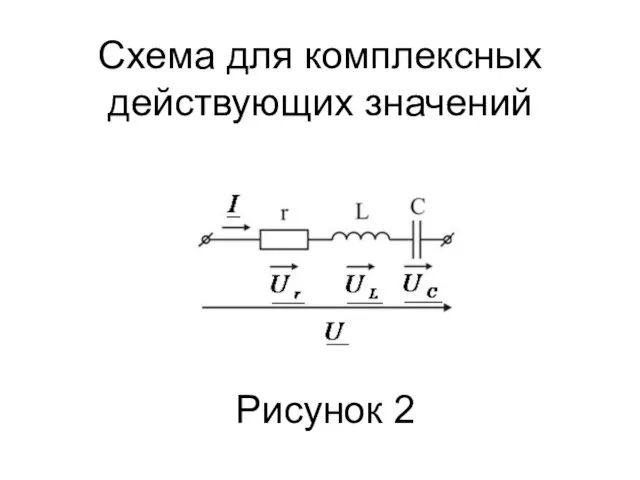
- 6. Схема для комплексных действующих значений Рисунок 2
- 7. Комплексные действующие значения напряжений: на резистор r: 2) на индуктивности L: 3) на емкости C: где
- 10. - уравнение по IIЗК для построения векторной диаграммы Рисунок 3 активно-индуктивный характер ЭЦ - реактивное сопротивление
- 11. - комплексное действующее значение реактивного напряжения; U – действующее напряжение цепи. (действующее значение)
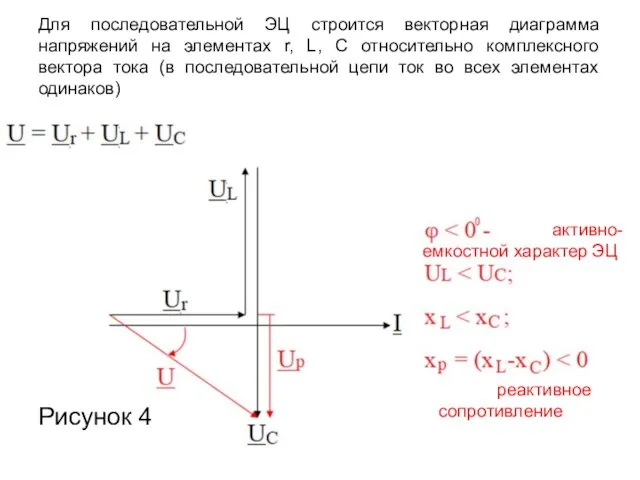
- 12. Рисунок 4 Для последовательной ЭЦ строится векторная диаграмма напряжений на элементах r, L, C относительно комплексного
- 13. - действующее значение напряжения электрической цепи - действующее реактивное напряжение цепи
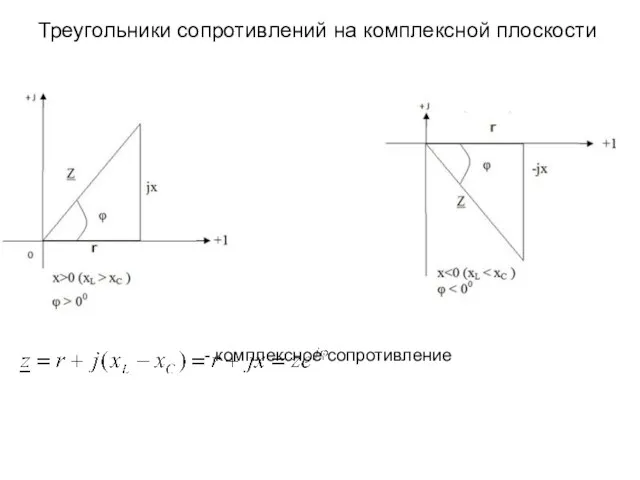
- 14. Треугольники сопротивлений на комплексной плоскости - комплексное сопротивление
- 15. - реактивное сопротивление - индуктивное сопротивление - емкостное сопротивление - угловая частота r – активное сопротивление
- 16. Знак угла сдвига фаз между напряжением и током цепи ϕ = ψu-ψi на векторной диаграмме тока
- 18. Скачать презентацию












 Презентация на тему Электролиты
Презентация на тему Электролиты Поздравляем вас, наши любимые мужчины!
Поздравляем вас, наши любимые мужчины! Баш3орт милли аштары
Баш3орт милли аштары История ислама
История ислама «Товаропроводящая цепочка фармацевтических препаратов. Где тонко, там и рвется (а где тонко?)».
«Товаропроводящая цепочка фармацевтических препаратов. Где тонко, там и рвется (а где тонко?)». Основные концепции культуры
Основные концепции культуры Декоративно- прикладное творчество народов Поволжья
Декоративно- прикладное творчество народов Поволжья Синхронный электродвигатель
Синхронный электродвигатель Мероприятия по энергосбережению в электрических сетях электроосвещения объектов капитального строительства
Мероприятия по энергосбережению в электрических сетях электроосвещения объектов капитального строительства КОНСТРУИРОВАНИЕ
КОНСТРУИРОВАНИЕ Зона смешанных и широколиственных лесов 8 класс
Зона смешанных и широколиственных лесов 8 класс Выставка марийских национальных костюмов
Выставка марийских национальных костюмов Особенности празднования Нового года в России
Особенности празднования Нового года в России Детская площадка
Детская площадка The system of State bodies of India
The system of State bodies of India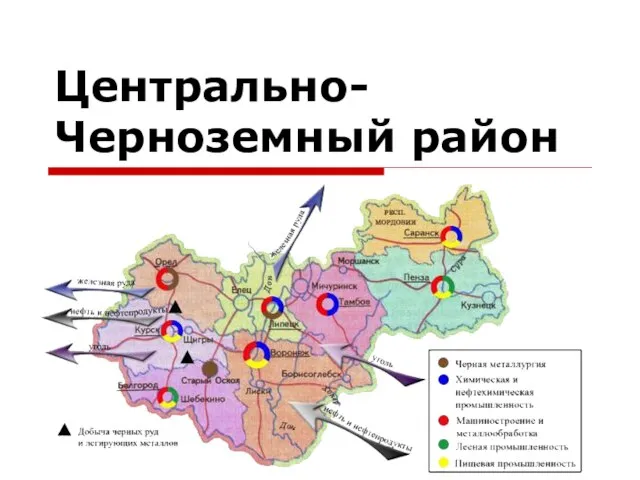 Центрально-Черноземный район
Центрально-Черноземный район Повторение. Чтение текста с изученными буквами
Повторение. Чтение текста с изученными буквами Конституционное право. Своя игра
Конституционное право. Своя игра Холодная прокатка труб (ХПТ).Краснов Денис
Холодная прокатка труб (ХПТ).Краснов Денис От кого же, мы всё же произошли?
От кого же, мы всё же произошли? Презентация_32
Презентация_32 Государственное общеобразовательное учреждение средняя общеобразовательная школа № 28 Василеостровского района
Государственное общеобразовательное учреждение средняя общеобразовательная школа № 28 Василеостровского района Туесок из стружки с геометрической резьбой
Туесок из стружки с геометрической резьбой Бизнес Мечты!
Бизнес Мечты! Typológia 3 - Letiská
Typológia 3 - Letiská Готовимся к
Готовимся к Апельсиновое настроение. Рисуем апельсины. Декоративный натюрморт в технике масляной живописи
Апельсиновое настроение. Рисуем апельсины. Декоративный натюрморт в технике масляной живописи Выпуск Эльгяйской СОШ 1972 года
Выпуск Эльгяйской СОШ 1972 года