Последовательности

Выпишем в порядке возрастания положительные четные числа
Первое такое число равно ?, второе - ?, третье - ?, четвёртое - ? и т.д.

Получим последовательность
2; 4; 6; 8; … .
На пятом месте в этой последовательности будет число ?, на десятом - ?, на сотом - ?

Для любого натурального числа п можно указать соответствующее ему положительное чётное число; оно равно 2п.

Еще одна последовательность
Выпишем в порядке убывания правильные дроби с числителем, равным 1: Какие это дроби?

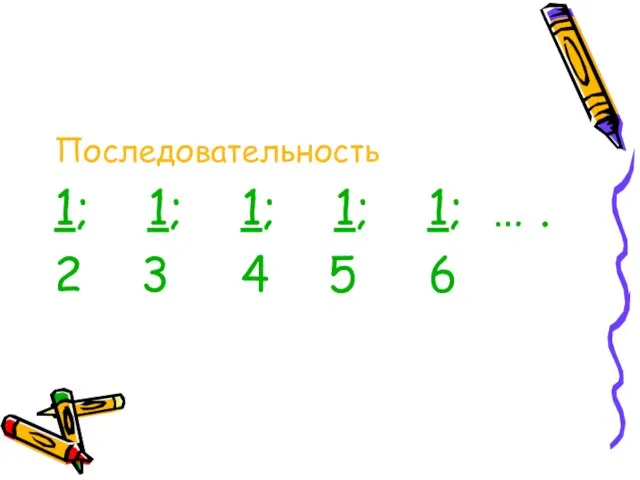
Последовательность
1; 1; 1; 1; 1; … .
2 3 4 5 6

Для любого натурального числа п можно указать соответствующую дробь, стоящую в этой последовательности на
п- м месте; она равна 1 .
п + 1
Так на шестом месте должна стоять дробь ?, на тридцатом - ?, на тысячном - ?

Определение:
Числа, образующие последовательность, называют членами последовательности.
Члены последовательности обозначаются буквами с индексами, указывающими порядковый номер члена, например: а 1, а 2, а 3, а 4, и т.д.
(читают так: «а первое , а второе, а третье , а четвертое и т.д.)

Член последовательности с номером п, или п- й член последовательности, обозначают а п, а саму последовательность - (а п)

Последовательности, содержащие бесконечно много членов, называются бесконечными.
Последовательности, содержащие конечное число членов, называют конечными. Например: конечной является последовательность двузначных чисел 10; 11; 12; 13; …; 98; 99.

Часто последовательность задают с помощью формулы п- го члена последовательности