Последовательности (можно ли объять необъятное…)

ОПРЕДЕЛЕНИЕ. Последовательностью называется функция натурального аргумента.
УРОК 1.
Определение
и
способы задания последовательности
СПОСОБЫ ЗАДАНИЯ:
словесный (описательный)
с помощью формулы n-ного члена
рекуррентный (“возвратный”)
графический

а) Последовательность натуральных чисел,
кратных 3
б) Последовательность правильных дробей
со знаменателем 7
в) Последовательность, все члены которой равны 1
г) Последовательность обыкновенных дробей
с числителем 1
Упражнения
{3; 6; 9; 12; …}
{1; 1; 1; …}

Упражнения

Последовательность Фибоначчи
a1 = 1, a2 = 1, an+2 = an+1 + an
Леонардо Пизанский
(1180 – 1240)
{1; 1; 2; 3; 5; 8; 13; 21;…; 144}
Формула n-ного члена
Проверьте справедливость формулы
для нескольких первых n

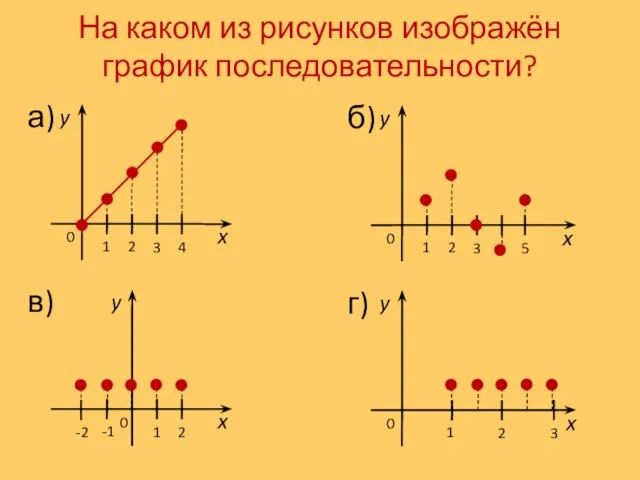
На каком из рисунков изображён
график последовательности?
2
3
1
б)
x
y
0
1
2
-1
в)
x
y
0
2
1
г)
x
y
0
5
-2
3

Тренировочные задания
ЗАДАЙТЕ ПОСЛЕДОВАТЕЛЬНОСТИ:
1) Словесным (описательным) способом:
а) {2; 3; 5; 7; 11; 13; …}
б) {1; 4; 9; 16; 25; …}
в) {1; 1; 1; …}
а) последовательность простых чисел
б) последовательность квадратов натуральных чисел
В) последовательность, все члены которой равны 1

Тренировочные задания
ЗАДАЙТЕ ПОСЛЕДОВАТЕЛЬНОСТИ:

Тренировочные задания
3) Назовите несколько первых членов последовательности, в которой:
а) a1 = 1, an+1 = an
б) a1 = 1, an+1 = an + 2
в) a1 = 1, a2 = 1, an+2 = an+1 + an
а) {1; 1; 1; …}
б) {1; 3; 5;…}
в) {1; 1; 2; 3;…}

Проверочная работа

Проверочная работа
2) Написать формулу n-ного члена:

Проверочная работа
Проверка
а)- 3; 15; - 27; 63.
б) 5; - 13; -21; 13.
в) -10; 2; -2; 14.
3) Написать первые четыре числа
последовательности {bn}, заданной рекуррентно:
а) b1 = –3, bn+1 = 9 – 2bn
б) b1 = 5, bn+1 = (–1)nbn – 8
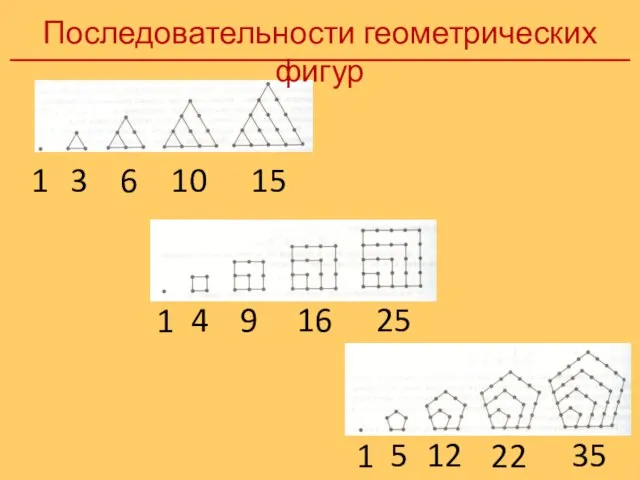
в) b1 = –10, b2 = 2, bn+2 = | bn | - 6bn+1

Последовательности геометрических фигур
1
3
6
10
15
1
1
9
16
25
4
5
12
22
35