Построение графиков функций, содержащих знак модуля

Содержание.
I. Введение.
II. Основная часть.
1) Понятия и определения.
2) Теоремы, следствия.
3) Построение графиков.
III. Заключение.
IV. Список используемой литературы.

I. Введение.
Объект исследования – математика.
Предмет исследования – функции, содержащие знак модуля.
Проблема исследования: построение графиков функций, содержащих модуль.
Цель исследования: получение более широких знаний о модуле числа, различных способах решения уравнений, содержащих знак абсолютной величины.
Задача исследования: использование различных методов исследования (теоретический, практический, исследовательский), расширение познавательного интереса к изучению алгебры, углубление знаний по теории модуля и решение задач, выходящих за страницы школьных учебников.

Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре - это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике - это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и т.п.
Модуль объемного сжатия (в физике) - отношение нормального напряжения в материале к относительному удлинению.

II. Основная часть.
Понятия и определения.
Чтобы глубоко изучать данную тему, необходимо познакомиться с простейшими определениями, которые мне будут необходимы:
Уравнение - это равенство, содержащее переменные.
Уравнение с модулем - это уравнение, содержащее переменную под знаком абсолютной величины (под знаком модуля). Например: |x|=1
Решить уравнение - это значит, найти все его корни, или доказать, что корней нет.
В математике модуль имеет несколько значений, но в моей исследовательской работе я возьму лишь одно из них.
Модулем или иначе абсолютной величиной отрицательного числа называется противоположное ему положительное число, модулем положительного числа и числа ноль называется само это число.

Теоремы
Теорема 1. Абсолютная величина действительного числа a≠0 равна большему из двух чисел a или -a.
Следствие 1. Из теоремы следует, что
|-a|=|a|.
Следствие 2. Для любого действительного числа a справедливы неравенства a≤|a| , -a≤|a|
Объединяя последние два неравенства в одно, получаем: -|a|≤a≤|a|

Теорема 2. Абсолютная величина любого действительного числа a равна арифметическому квадратному корню из a2 : |a|=√a2
Эта теорема дает возможность при решении некоторых задач заменять |a| на √a2
Геометрически |a| означает расстояние на координатной прямой от точки, изображающей число a, до начала отсчета.
Если a≠0 то на координатной прямой существует две точки a и -a, равноудаленной от нуля, модули которых равны.
Если a = 0, то на координатной прямой |a| изображается точкой 0.

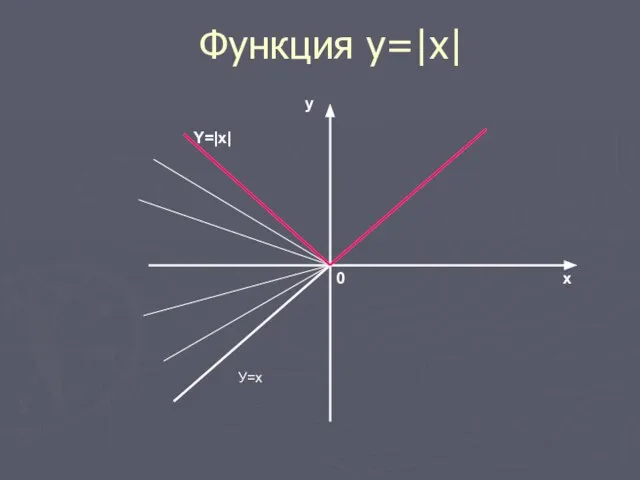
Функция у =|х|
График функции у =|х| получается из графика
у=х следующим образом: часть графика у=х, лежащая над осью х, сохраняется, часть его, лежащая ниже оси х , отображается симметрично относительно оси х.

Функция у=|x|
х
у
0
У=х
Y=|x|

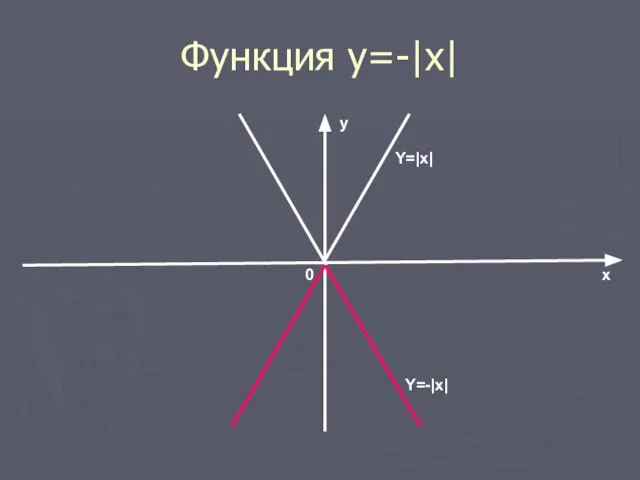
Функция y=-|x|
График функции
y=-|x| получается симметричным отображением графика y=|x| относительно оси х.

Функция у=-|x|
x
y
0
Y=|x|
Y=-|x|

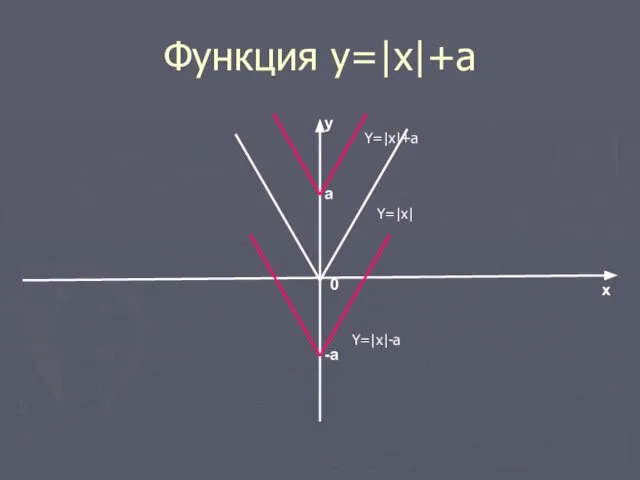
Функция у=|х|+а
График функции у=|х|+а получается параллельным переносом графика у=|х| в положительном направлении оси у на а единицу отрезка при а>0 и в отрицательном направлении на |а| при а<0.

Функция у=|x|+a
a
-a
0
x
y
Y=|x|
Y=|x|+a
Y=|x|-a

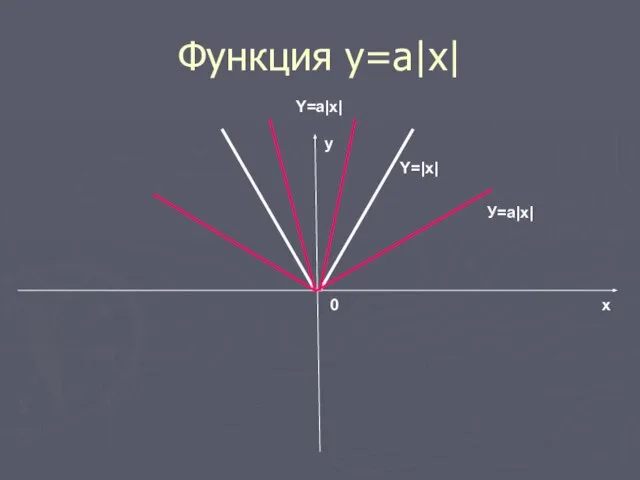
Функция у=а|х|
График функции у=а|х| получается растяжением графика у=|х| вдоль оси у в а раз при а>1 и сжатием вдоль этой оси в 1\а раз при 0

Функция y=a|x|
x
y
0
У=a|x|
Y=|x|
Y=a|x|

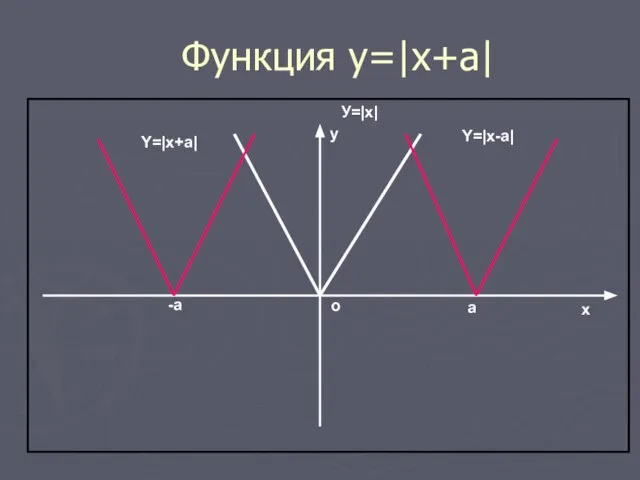
Функция у=|x+a|
График функции у=|x+a| получается параллельным переносом графика y=|x| в отрицательном направлении от оси х на |x| при а>0 и в положительном направлении на |a| при a<0.

Функция y=|x+a|
о
х
у
У=|x|
-a
a
Y=|x+a|
Y=|x-a|

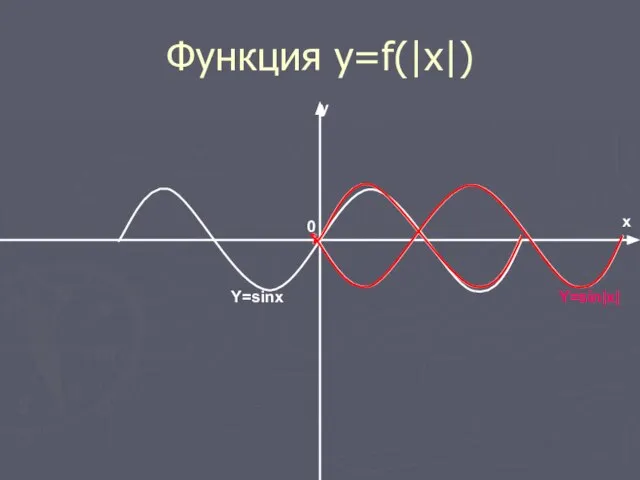
Функция y=f(|x|)
График функции y=f(|x|) получается из графика y=f(x) следующим образом:1) при х>0 график f(x) сохраняется, 2) при x<0, полученная часть графика отображается симметрично относительно оси у.

Функция y=f(|x|)
Y=sinx
Y=sin|x|
0
y
x

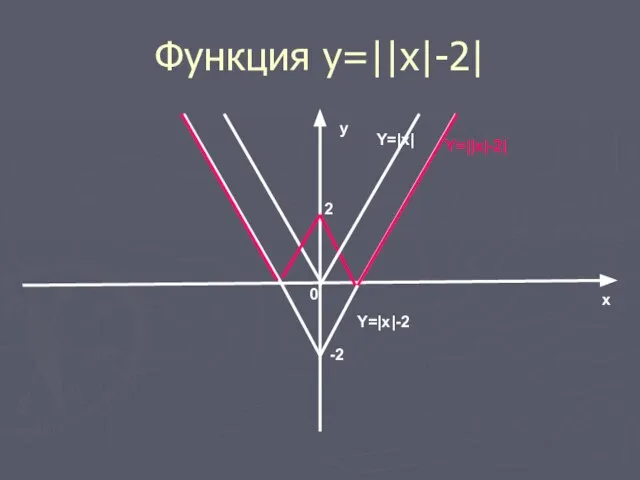
От теории к практике
Рассмотрим построение более сложных графиков.
Построить график функции у=||x|+2|.
Построение.
1) Строим график y=|x|
2)Смещаем его по оси у вниз на 2 ед.отр.
3)Отображаем часть графика, расположенного под осью х, симметрично этой оси, в верхнюю полуплоскость.

Функция у=||x|-2|
x
y
0
-2
2
Y=|x|
Y=|x|-2
Y=||x|-2|

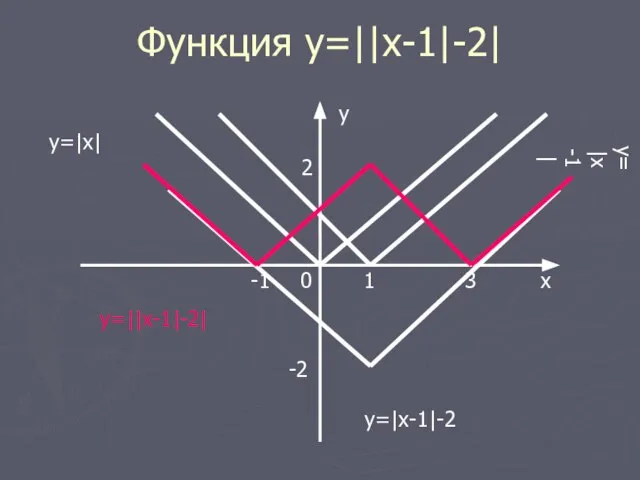
Функция y=||x-1|-2|
Построение.
1)Строим график функции y=|x|.
2)Строим график функции y=|x-1|.
3)Строим график функции y= |x-1|-2.
4)Применяем к графику y=|x-1|-2 операцию “модуль”.

Функция y=||x-1|-2|
x
y=|x|
y
0
1
y=|x-1|
-1
3
2
-2
y=|x-1|-2
y=||x-1|-2|

Функция y=|x²-4|x|-3|
Построение.
1)Строим график y=x²-4x+3
2)y=x²-4|x|+3 — отражаем полученный график в п.1 относительно оси ординат. Функция чётная.
3)y=|x²-4|x|+3| — часть графика, расположенную в нижней полу плоскости,
отражаем относительно оси абсцисс. Полученная в верхней полуплоскости линия и будет графиком заданной функции.

Функция y=|x²-4|x|+3|
y
x
0
-1
-3
1
3
3
y=x²-4x+3
y=x²-4|x|+3
y=|x²-4|x|+3|

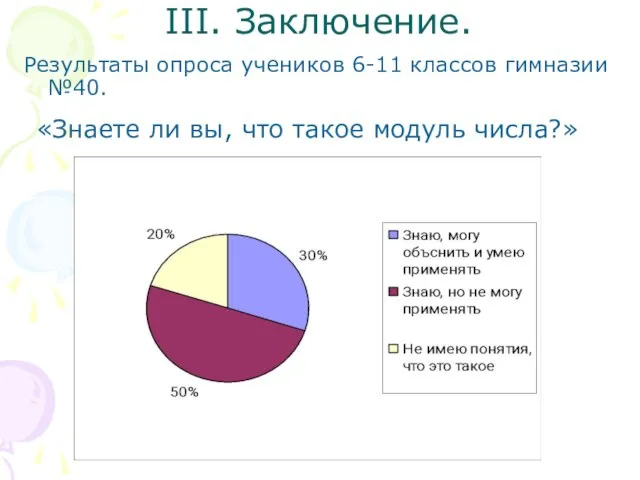
III. Заключение.
Результаты опроса учеников 6-11 классов гимназии №40.
«Знаете ли вы, что такое модуль числа?»

Мой научно-исследовательский проект можно использовать:
1) на уроках алгебры в 7-9 классах;
2) для индивидуального изучения понятия темы «модуль числа»;
3) групповых и факультативных занятиях;
4) для подготовки к экзаменам.

Мой научно-исследовательский проект будет полезен в работе:
ученикам
учителям. Он поможет отыскать новые пути совершенствования обычного школьного урока.