Содержание
- 2. Правильные многоугольники привлекали внимание древнегреческих учёных ещё задолго да Архимеда. Пифагорейцы, выбравшие эмблемой своего союза пентаграмму
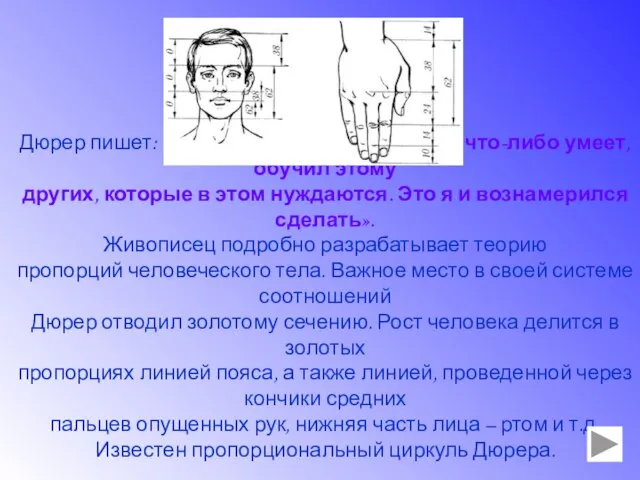
- 3. Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это
- 4. Леонардо да Винчи также много писал о многоугольниках, но именно Дюрер, а не Леонардо, передал средневековые
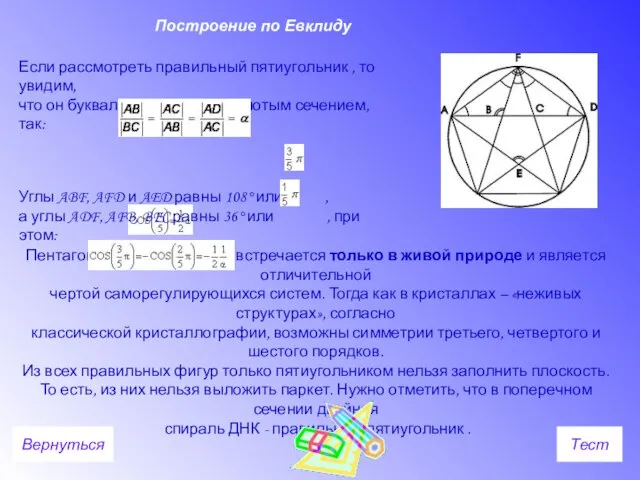
- 5. Предложенное Евклидом построение правильного пятиугольника включает в себя деление отрезка прямой в среднем и крайнем отношении,
- 6. Способы построение пятиугольника По Дюреру По Евклиду
- 7. Пентагональная симметрия встречается только в живой природе и является отличительной чертой саморегулирующихся систем. Тогда как в
- 8. Приближенное построение правильного пятиугольника представляет собой интерес. А.Дюрером оно проводится при условии неизменности раствора циркуля, что
- 9. A B C D E F G H J K Вернуться Попробуем выполнить построение Дюрера самостоятельно:
- 10. Тест 1. Что представляет собой пентаграмма? Звезда Рукопись Пирамида
- 11. Верно!Поздравляю! Следующий вопрос
- 12. Неверно!Попробуйте еще раз! Вернуться к вопросу!
- 13. 2. Кто из перечисленных ученых не исследовал пятиугольники? Коперник Евклид Дюрер
- 14. Правильно! Следующий вопрос
- 15. Подумайте! Вернуться к вопросу!
- 16. 3. Как называется великий труд Евклида? «Основы геометрии» «Пентаграммы» «Начала»
- 17. Молодец! Следующий вопрос
- 18. Неправильно! Вернуться к вопросу!
- 19. 4. Где встречается пентагональная симметрия? В неживой природе В живой природе В учебнике геометрии
- 20. Умница! Выйти из теста
- 21. Неверно!Попробуйте еще раз! Вернуться к вопросу!
- 22. Выполнила Бурова Елена ученица 9Б класса МОУ «Лицей №43» Проверила Лобанова О. Е. учитель алгебры и
- 24. Скачать презентацию

















 В мире боевых искусств
В мире боевых искусств Политические партии
Политические партии Zrozumieć kobietę
Zrozumieć kobietę Северный Ледовитый океан 7 класс
Северный Ледовитый океан 7 класс Образование в области прав ребенка как мультикультурный проект
Образование в области прав ребенка как мультикультурный проект Государство как субъект МЧП. Лекция 7
Государство как субъект МЧП. Лекция 7 Сложные проценты на фондовом рынке
Сложные проценты на фондовом рынке Измерительная техника
Измерительная техника Колобок в стране
Колобок в стране Современные масс-медиа о событиях Второй Мировой войны: структурный анализ дискурса вражды
Современные масс-медиа о событиях Второй Мировой войны: структурный анализ дискурса вражды Презентация на тему Симметрия в природе
Презентация на тему Симметрия в природе Would you like to join our sport club?
Would you like to join our sport club? Департамент специальных событий
Департамент специальных событий Структура питч-презентации
Структура питч-презентации Волшебные нотки
Волшебные нотки Клубы по интересам
Клубы по интересам  Л.В. Чайка, методист ГРЦИО «Тьютор»
Л.В. Чайка, методист ГРЦИО «Тьютор» Господин Митюков и его стипендии
Господин Митюков и его стипендии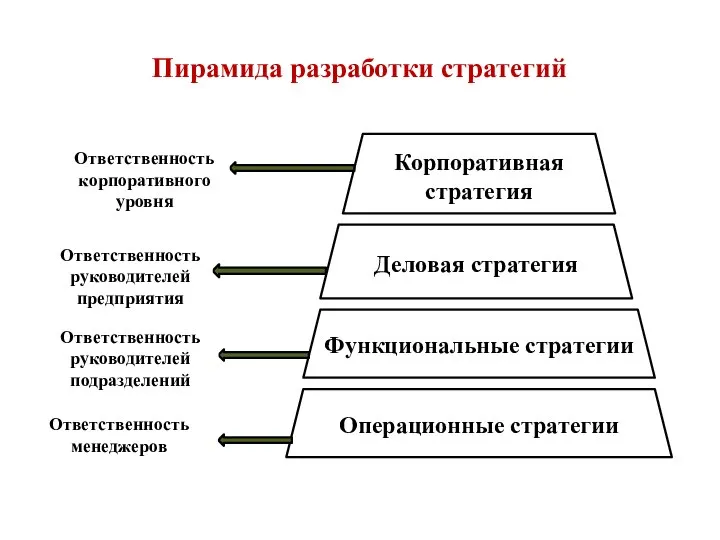 Пирамида разработки стратегий
Пирамида разработки стратегий Презентация
Презентация Презентация по английскому Использование smart board на уроках английского языка
Презентация по английскому Использование smart board на уроках английского языка  Магнитное поле тока
Магнитное поле тока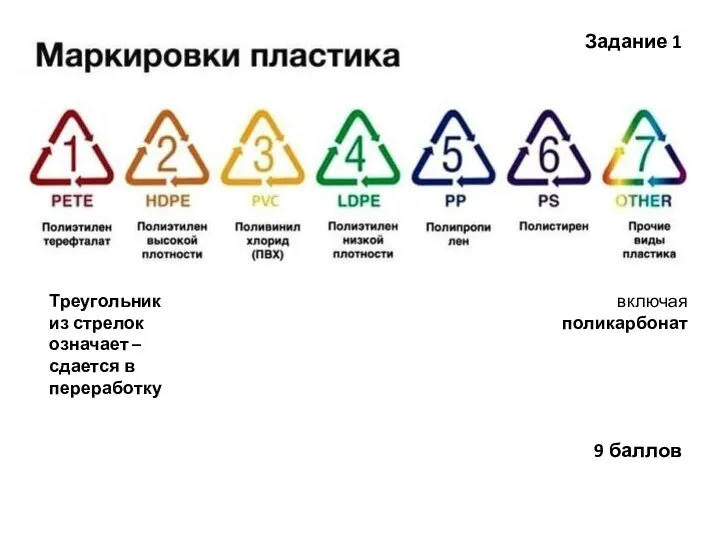 Маркировка пластика
Маркировка пластика Самопрезентация. Пермякова Анастасия Даниловна
Самопрезентация. Пермякова Анастасия Даниловна Фитоиндикация типов леса по А. С. Барабанщикову по Д. А. Цыганову в сравнении с Погребняком
Фитоиндикация типов леса по А. С. Барабанщикову по Д. А. Цыганову в сравнении с Погребняком Иконы Богородицы в истории России
Иконы Богородицы в истории России Федеральный государственный образовательный стандарт общего образования: актуальные вопросы введенияИюль 2010 г.
Федеральный государственный образовательный стандарт общего образования: актуальные вопросы введенияИюль 2010 г. Что такое КПК. Зачем нужен кредитный потребительский кооператив
Что такое КПК. Зачем нужен кредитный потребительский кооператив