Содержание
- 2. Фазовая теория рассеяния Рассеяние на изотропном потенциале Разложение волновой функции по парциальным волнам Радиальная часть Rl
- 3. Разложение плоской волны Сферические функции Бесселя jl, j0(x)=sin(x)/x jl(x)=(π /2x)Jl+1/2(x) Разложение ψ(r)
- 4. Амплитуда рассеяния S матрица Парциальная амплитуда Разложение амплитуды рассеяния
- 5. Сечение рассеяния Парциальное сечение Максимальное парциальное сечение
- 6. Условие унитарности Парциальная волна Расходящаяся волна Сходящаяся волна Суперпозиция парциальных волн Матрица рассеяния S Унитарность S
- 7. Оптическая теорема
- 8. Закон сохранения числа частиц Плотность потока частиц
- 9. Условие унитарности S матрицы в представлении плоских волн
- 10. Приближение Борна Условие приближения Вероятность рассеяния
- 11. Квазиклассическое приближение Квазиклассический предел Классические траектории движения Классическое сечение рассеяния
- 12. Приближение WKB, Приближение эйконала Квазиклассическая волновая функция Квазиклассическая фаза рассеяния
- 13. Эйконал Квазиклассическая фаза рассеяния
- 14. Квазиклассическая амплитуда рассеяния Замена переменных
- 15. Борновский предел Сечение рассеяния
- 16. Рассеяние медленных частиц ka Волновая функция вне действия потенциала r >> a Волновая функция в области
- 17. Сшивание волновых функций a
- 18. Резонансное рассеяние медленных частиц резонанс в s - волне, l = 0 Условие резонанса,
- 20. резонанс с l ≠ 0
- 21. Аналитические свойства S матрицы k → -k
- 22. t → -t Вещественная ось Мнимая ось
- 23. Особенности S матрицы Полюса S матрицы, связанные состояния E=E0 Пример: резонанс в s - волне, ka
- 24. Положение полюсов k0=k’+ik”: k” >0, k’=0; k” Условие непрерывности
- 25. Полюса на нефизическом листе k”
- 26. Свойства вычетов Полюс на физическом листе k0=iκ Связанное состояние с энергией и волновой функцией Волновая функция
- 27. Условие непрерывности
- 28. Теорема Левинсона Функция Йоста Dl(k)
- 29. Квазистационарные состояния Энергия состояния Волновая функция Временная зависимость волновой функции Пространственная зависимость волновой функции
- 30. Условие непрерывности
- 31. Квазистационарное состояние в задаче рассеяния Полюса на нефизическом листе k”
- 33. Зависимость волновой функции рассеяния от энергии налетающий частицы в области резонанса
- 34. Время соударения
- 35. Координатная и энергетическая зависимость волновой функции задачи рассеяния в области резонанса Резонанс в неупругом рассеянии
- 37. Многоканальное рассеяние Волновая функция многоканальной задачи Если E > Λi - i канал рассеяния открыт, Im{ki}=0.
- 38. Сечения рассеяния, разложение по парциальным волнам Волновая функция на бесконечности - амплитуда рассеяния
- 39. Дифференциальные сечение рассеяния Полные сечение рассеяния Сечение упругого рассеяния Сечение неупругого рассеяния Полное сечение
- 40. Условие унитарности - парциальная волна с моментом l Закон сохранения числа частиц:
- 42. Оптическая теорема
- 43. Обратимость времени, теорема взаимности t → -t Ψ → Ψ* Условие унитарности Симметричность S - матрицы
- 44. Аналитические свойства Точки ветвления Полюса на физическом листе E 0 Связанные состояния E = E0 Волновая
- 45. Условие непрерывности
- 46. Формула Брейта - Вигнера Условие унитарности Γi=vi|Ai|2 - парциальная ширина, Γ = Σi Γi - полная
- 47. Рассеяние через образование промежуточного квазистационарного состояния, прямое рассеяние Сечение образования промежуточного квазистационарного состояния в пренебрежении каналом
- 48. Резонансы формы Пример: Неупругое резонансное рассеяние с возбуждением мишени
- 49. Резонансы Фешбаха Пример: Резонансное рассеяние с образованием автоионизационного состояния. + Автоионизационная ширина Неупругая ширина Сечение резонансного
- 50. Оптическая модель рассеяния Большое число плотно расположенных резонансов Усредненные сечения, l=0 Усреднение S матрицы, Γ Принцип
- 51. Пороговые явления E ≈ Λi, Ti= E - Λi → 0 Пример: i=1,2; E ≈ Λ,
- 52. Волновая функция ψ(+) в классически недоступной области r Закон 1/v и теория возмущений
- 53. Пороговое поведение сечения рождения заряженных частиц. 1. Притяжение, qxqy l2 Волновая функция ψ(+) в классически недоступной
- 54. Поведение упругого сечения вблизи порога E ≈ Λ2 1. E Λ2 2. E Λ2
- 55. Дифференциальное сечение рассеяния E Λ2, E Λ2. { sin(2δ0-α) E Λ2, cos(2δ0-α) E
- 56. Взаимодействие в конечном состоянии при реакциях Резонанс при рождении медленных частиц
- 58. Скачать презентацию

















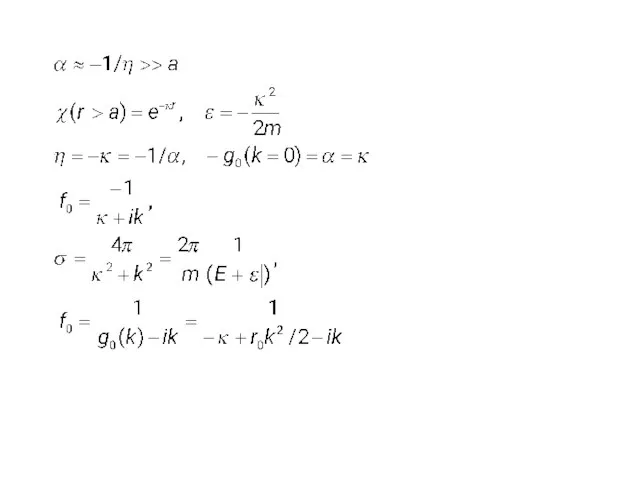
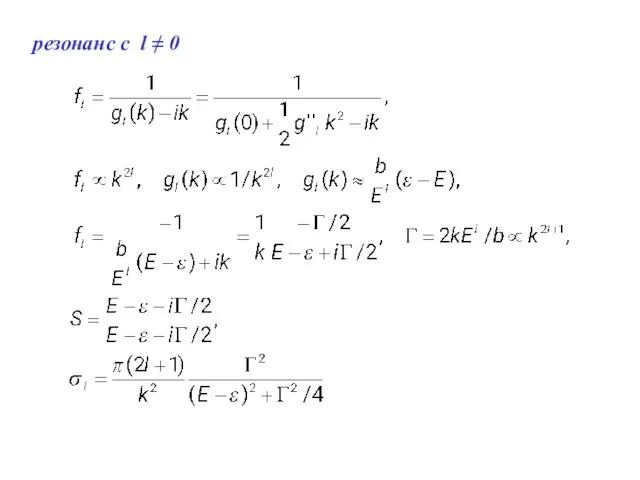




















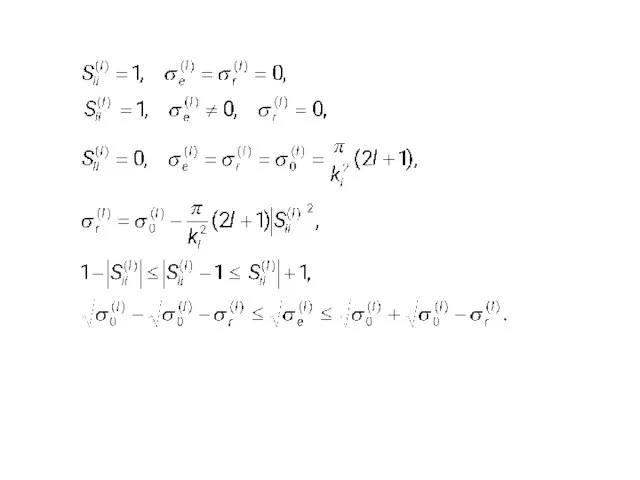















 Презентация на тему ФГОС как методология новой парадигмы образования
Презентация на тему ФГОС как методология новой парадигмы образования  20170307_strany_severnoy_evropy
20170307_strany_severnoy_evropy Путешествия и географические открытия
Путешествия и географические открытия Поле чудес «Сказки Пушкина»
Поле чудес «Сказки Пушкина» Живая связь времен
Живая связь времен Структура коммуникации. Теоретические модели коммуникации
Структура коммуникации. Теоретические модели коммуникации Medelyaevoy_Vlady
Medelyaevoy_Vlady Everyday slang. Сленг на каждый день
Everyday slang. Сленг на каждый день Презентация на тему История развития экологии
Презентация на тему История развития экологии Синдром патологического влечения к ПАВ
Синдром патологического влечения к ПАВ Папоротникообразные
Папоротникообразные Спонсорство – деньги на ветер или увеличение продаж
Спонсорство – деньги на ветер или увеличение продаж The II International festival-forum
The II International festival-forum Игровая программа Смак
Игровая программа Смак Жизнь и творчество Александра Сергеевича Грибоедова
Жизнь и творчество Александра Сергеевича Грибоедова Роль права в жизни человека, общества и государства
Роль права в жизни человека, общества и государства Брейнсторминг (brainstorming)
Брейнсторминг (brainstorming) Генерал М. Тучков
Генерал М. Тучков "О подходах к разработке основ бизнес-синергетики лидерства, управления и конкурентоспособности для экономики Казахстана" Доклад
"О подходах к разработке основ бизнес-синергетики лидерства, управления и конкурентоспособности для экономики Казахстана" Доклад Презентация на тему Правила поведения ученика
Презентация на тему Правила поведения ученика Умник
Умник С и м в о л ы Р о с с и и
С и м в о л ы Р о с с и и Обесценивание мыслей, чувств и эмоций ребенка
Обесценивание мыслей, чувств и эмоций ребенка Ультрафиолетовые лучи
Ультрафиолетовые лучи ИНФОРМАЦИОННАЯ МОДЕЛЬ СИСТЕМЫ
ИНФОРМАЦИОННАЯ МОДЕЛЬ СИСТЕМЫ Декоративные цветы. История развития
Декоративные цветы. История развития Общие, должностные и специальные обязанности военнослужащих
Общие, должностные и специальные обязанности военнослужащих ИССЛЕДОВАНИЕ ПОТРЕБИТЕЛЬСКИХ НАСТРОЕНИЙ ПЕРМЯКОВ Агентство «Коммерческие Консультации и Исследования»
ИССЛЕДОВАНИЕ ПОТРЕБИТЕЛЬСКИХ НАСТРОЕНИЙ ПЕРМЯКОВ Агентство «Коммерческие Консультации и Исследования»