Поверхности. Начертательная геометрия

ПОВЕРХНОСТИ
основные понятия и определения
ПОВЕРХНОСТЬ – множество всех последовательных положений движущейся линии.
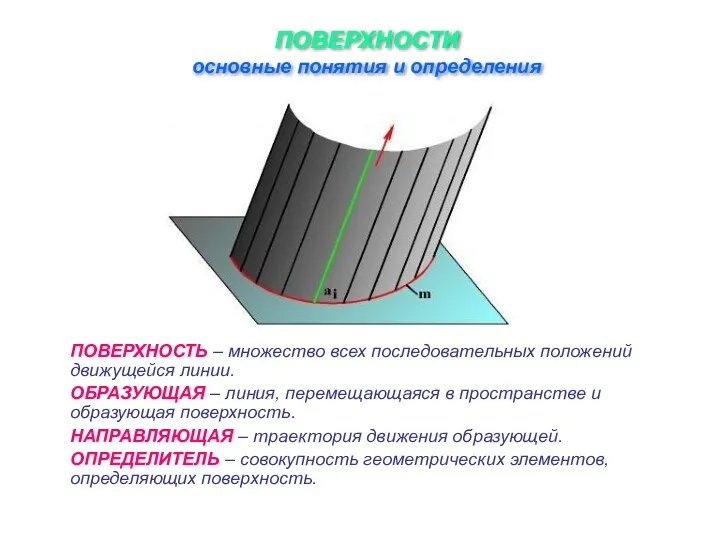
ОБРАЗУЮЩАЯ – линия, перемещающаяся в пространстве и образующая поверхность.
НАПРАВЛЯЮЩАЯ – траектория движения образующей.
ОПРЕДЕЛИТЕЛЬ – совокупность геометрических элементов, определяющих поверхность.

КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ

ЛИНЕЙЧАТЫЕ И НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ
ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ – это поверхности с прямолинейной образующей.
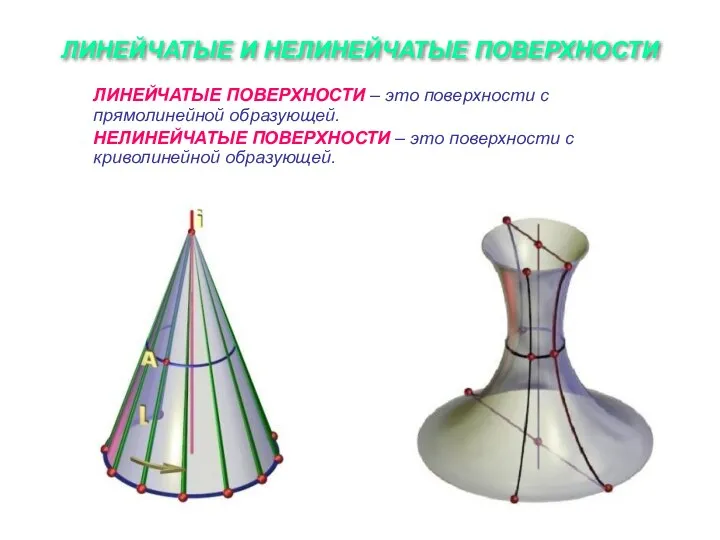
НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ – это поверхности с криволинейной образующей.

РАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ
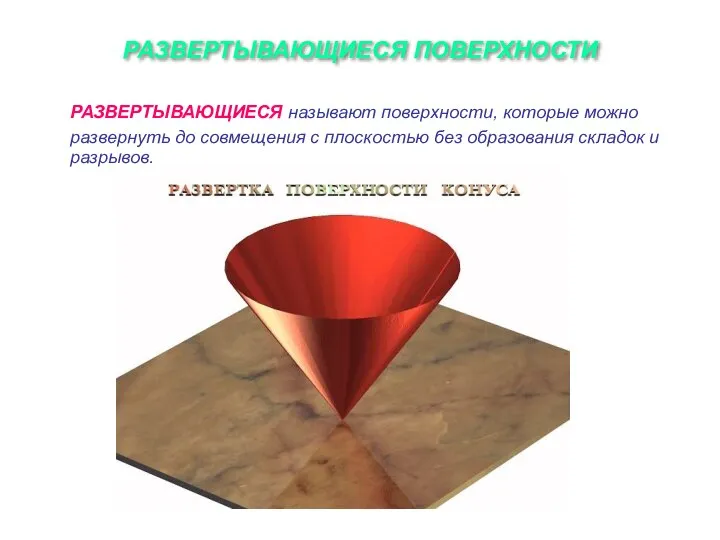
РАЗВЕРТЫВАЮЩИЕСЯ называют поверхности, которые можно развернуть до совмещения с плоскостью без образования складок и разрывов.

НЕРАЗВЕРТЫВАЮЩИЕСЯ ПОВЕРХНОСТИ
НЕРАЗВЕРТЫВАЮЩИЕСЯ называют поверхности, которые при совмещении с плоскостью образуют складки или разрывы.

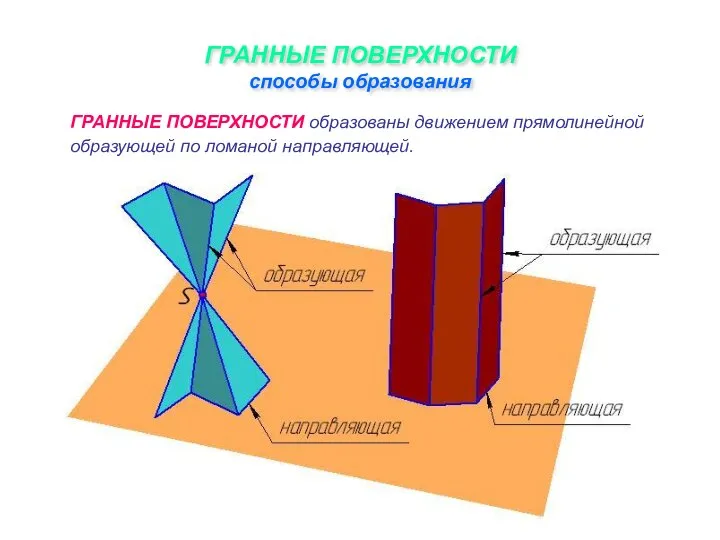
ГРАННЫЕ ПОВЕРХНОСТИ
способы образования
ГРАННЫЕ ПОВЕРХНОСТИ образованы движением прямолинейной образующей по ломаной направляющей.

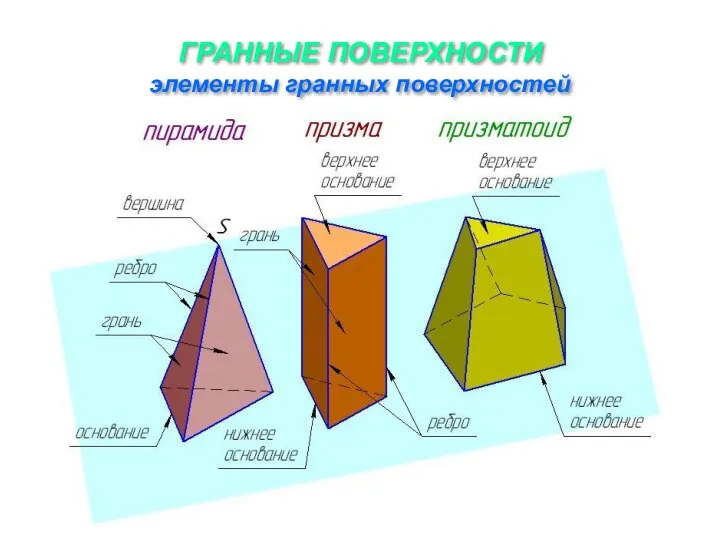
ГРАННЫЕ ПОВЕРХНОСТИ
элементы гранных поверхностей

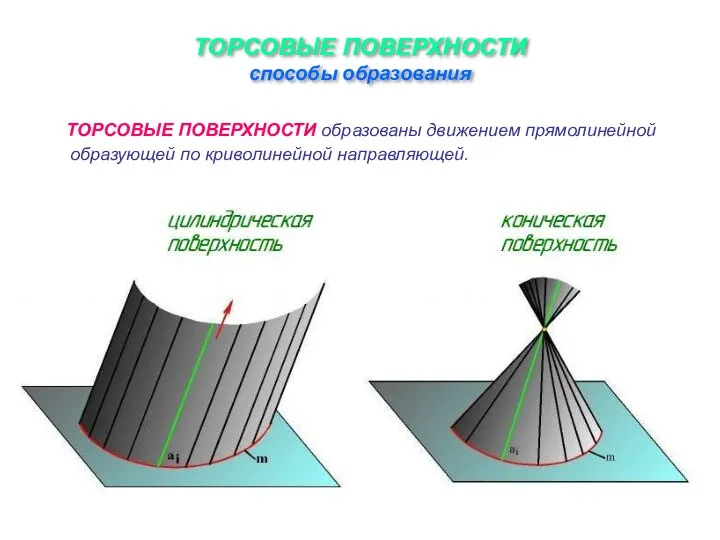
ТОРСОВЫЕ ПОВЕРХНОСТИ
способы образования
ТОРСОВЫЕ ПОВЕРХНОСТИ образованы движением прямолинейной образующей по криволинейной направляющей.

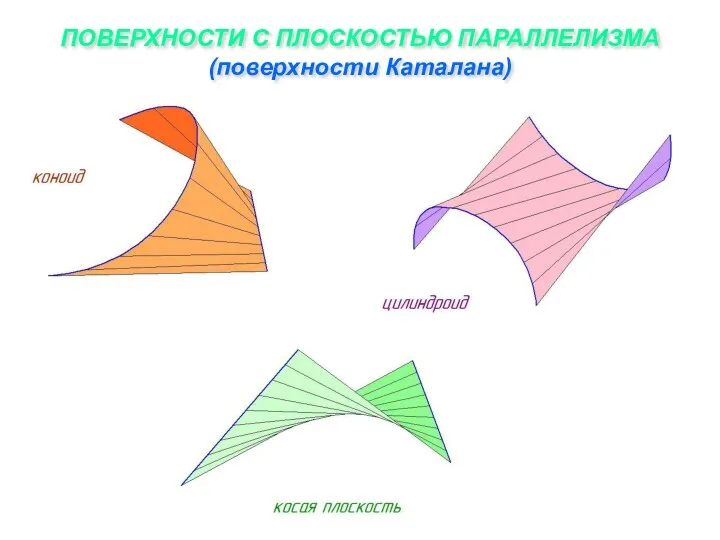
ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ ПАРАЛЛЕЛИЗМА
(поверхности Каталана)

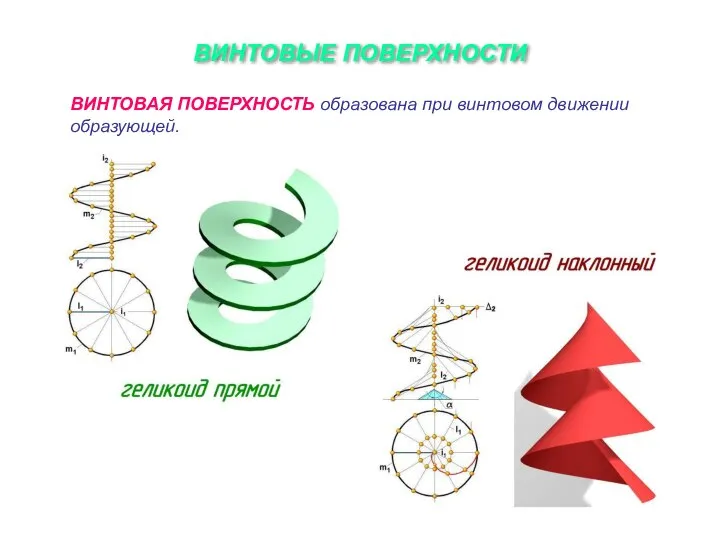
ВИНТОВЫЕ ПОВЕРХНОСТИ
ВИНТОВАЯ ПОВЕРХНОСТЬ образована при винтовом движении образующей.

ПОВЕРХНОСТИ ВРАЩЕНИЯ
способы образования
ПОВЕРХНОСТЬ ВРАЩЕНИЯ – это поверхность, образованная вращением образующей вокруг неподвижной оси.

ПОВЕРХНОСТИ ВРАЩЕНИЯ
основные элементы поверхностей вращения
ПАРАЛЛЕЛЬ – окружность, образованная вращением точки вокруг оси.
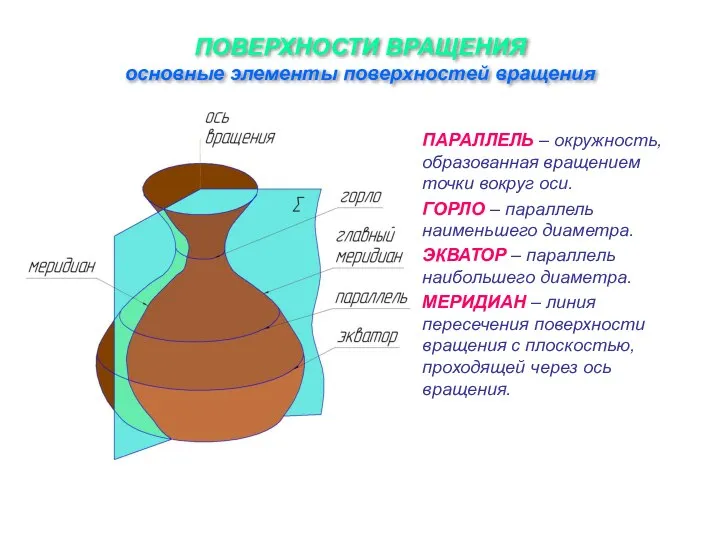
ГОРЛО – параллель наименьшего диаметра.
ЭКВАТОР – параллель наибольшего диаметра.
МЕРИДИАН – линия пересечения поверхности вращения с плоскостью, проходящей через ось вращения.

ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИ
ЦИКЛИЧЕСКИЕ ПОВЕРХНОСТИ образованы при движении произвольной кривой (окружности) вдоль направляющей.
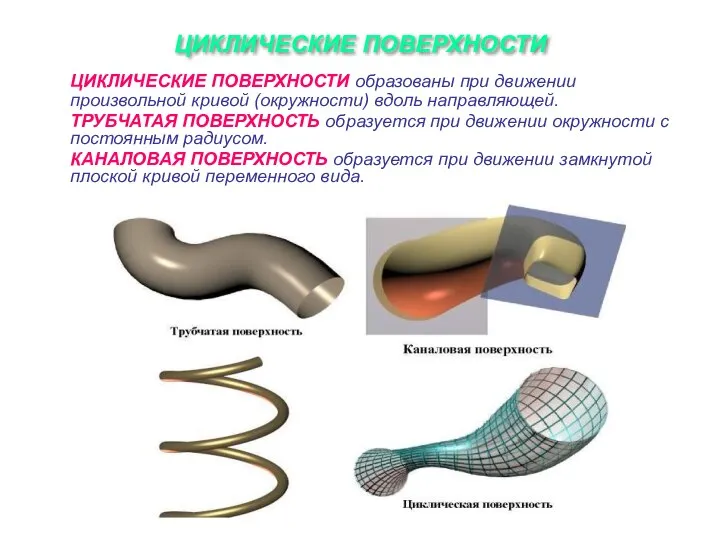
ТРУБЧАТАЯ ПОВЕРХНОСТЬ образуется при движении окружности с постоянным радиусом.
КАНАЛОВАЯ ПОВЕРХНОСТЬ образуется при движении замкнутой плоской кривой переменного вида.

ГРАФИЧЕСКИЕ ПОВЕРХНОСТИ
ГРАФИЧЕСКИЕ ПОВЕРХНОСТИ задаются конечным множеством линий уровня, образующих каркас этих поверхностей.

ТОЧКА НА ПОВЕРХНОСТИ
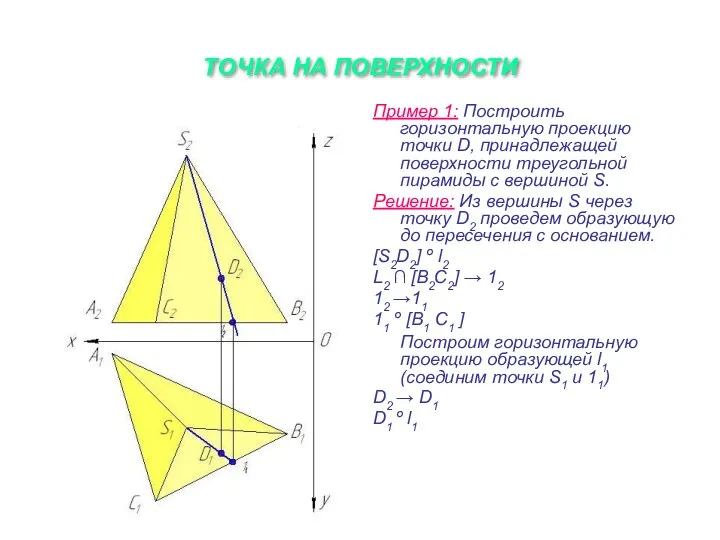
Пример 1: Построить горизонтальную проекцию точки D, принадлежащей поверхности треугольной пирамиды с вершиной S.
Решение: Из вершины S через точку D2 проведем образующую до пересечения с основанием.
[S2D2] º l2
L2 ∩ [B2C2] → 12
12 →11
11 º [B1 C1 ]
Построим горизонтальную проекцию образующей l1 (соединим точки S1 и 11)
D2 → D1
D1 º l1

ТОЧКА НА ПОВЕРХНОСТИ
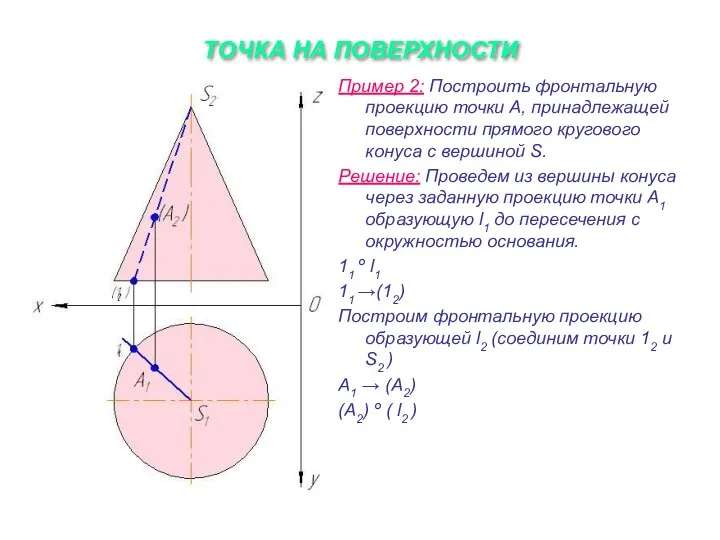
Пример 2: Построить фронтальную проекцию точки А, принадлежащей поверхности прямого кругового конуса с вершиной S.
Решение: Проведем из вершины конуса через заданную проекцию точки А1 образующую l1 до пересечения с окружностью основания.
11 º l1
11 →(12)
Построим фронтальную проекцию образующей l2 (соединим точки 12 и S2 )
А1 → (А2)
(А2) º ( l2 )

ТОЧКА НА ПОВЕРХНОСТИ
Пример 3: Построить фронтальную проекцию точки А, принадлежащей поверхности сферы.
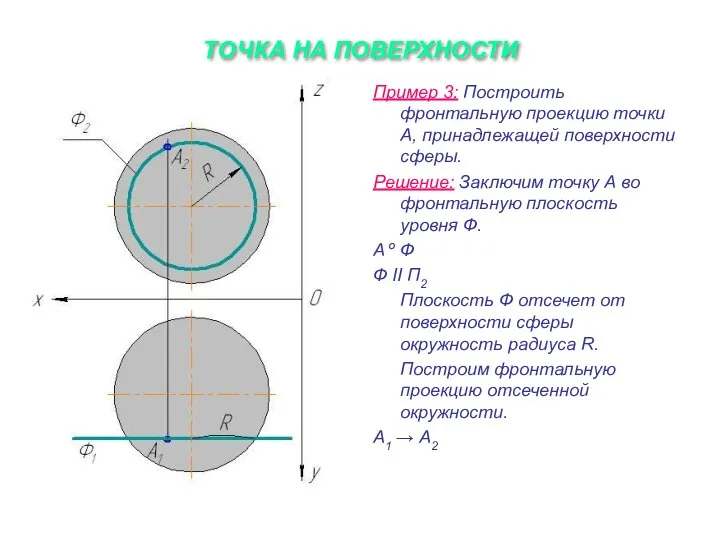
Решение: Заключим точку А во фронтальную плоскость уровня Ф.
А º Ф
Ф ІІ П2
Плоскость Ф отсечет от поверхности сферы окружность радиуса R.
Построим фронтальную проекцию отсеченной окружности.
А1 → А2

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ
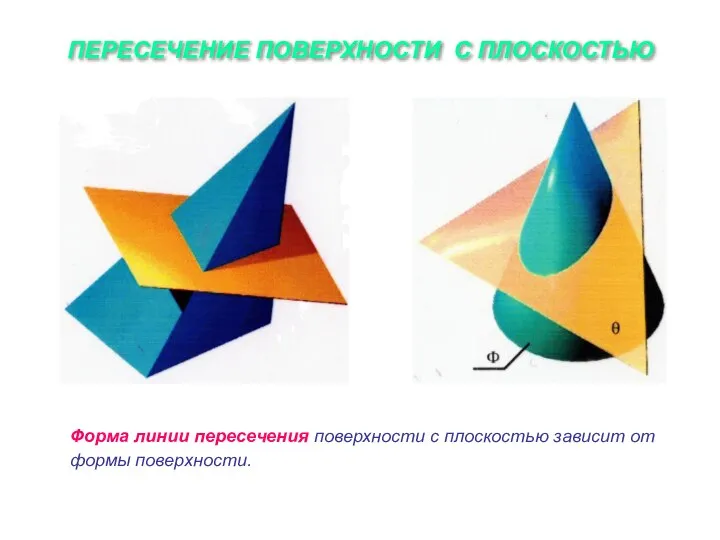
Форма линии пересечения поверхности с плоскостью зависит от формы поверхности.

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ
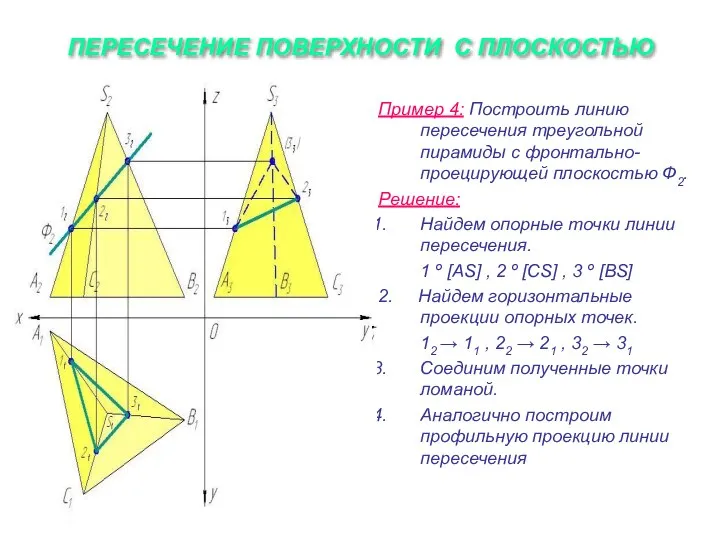
Пример 4: Построить линию пересечения треугольной пирамиды с фронтально-проецирующей плоскостью Ф2.
Решение:
Найдем опорные точки линии пересечения.
1 º [AS] , 2 º [CS] , 3 º [BS]
2. Найдем горизонтальные проекции опорных точек.
12 → 11 , 22 → 21 , 32 → 31
Соединим полученные точки ломаной.
Аналогично построим профильную проекцию линии пересечения

ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТИ С ПЛОСКОСТЬЮ
Пример 5: Построить линию пересечения поверхности сферы с горизонтально проецирующей плоскостью Г.
Решение: 1. Найдем опорные точки линии пересечения.
2. Построим фронтальные проекции опорных точек
11→(12) , 21→22 , (2/1)→2/2 , 41→42
31 º Ф1 , (3 /1 ) º Ф1 , Ф ІІ П2
3. Построим вспомогательную окружность радиусом R.
4. Спроецируем на эту окружность точки 31→32 , (3 /1)→3 /2
5. Соединить лекальной кривой построенные точки, учитывая их видимость.
6. Аналогично строим профильную проекцию линии пересечения.