Поверхности вращения

Поверхность α , образованная вращением образующей ℓ вокруг неподвижной оси i, называется поверхностью вращения

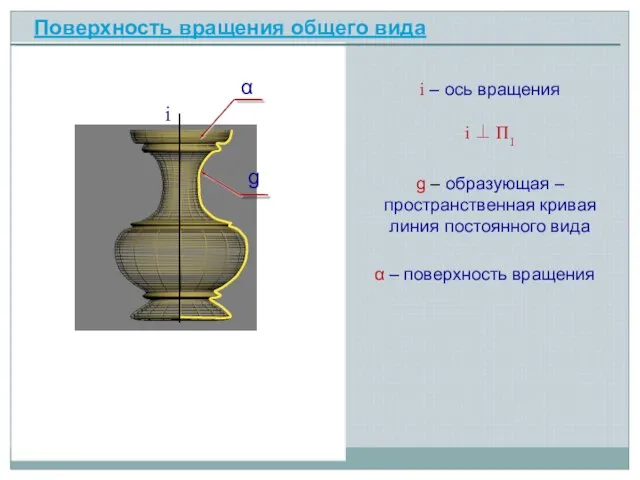
i – ось вращения
Поверхность вращения общего вида
i
g – образующая – пространственная кривая линия постоянного вида
g
α – поверхность вращения
α
i ⊥ П1

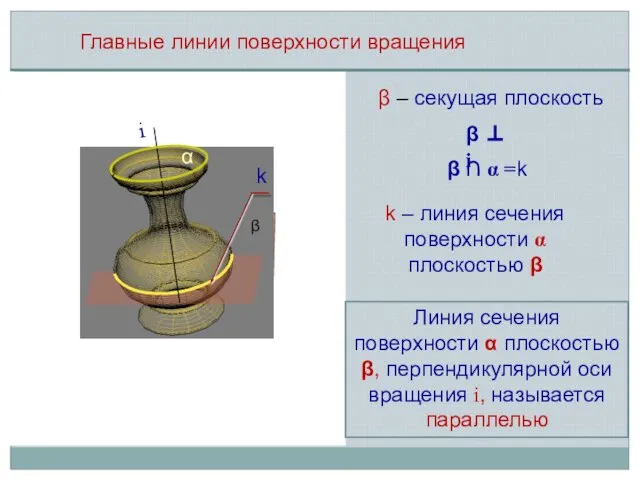
β – секущая плоскость
Главные линии поверхности вращения
k – линия сечения поверхности α плоскостью β
k
i
β ⊥ i
Линия сечения поверхности α плоскостью β, перпендикулярной оси вращения i, называется параллелью
β
β ∩ α =k
α

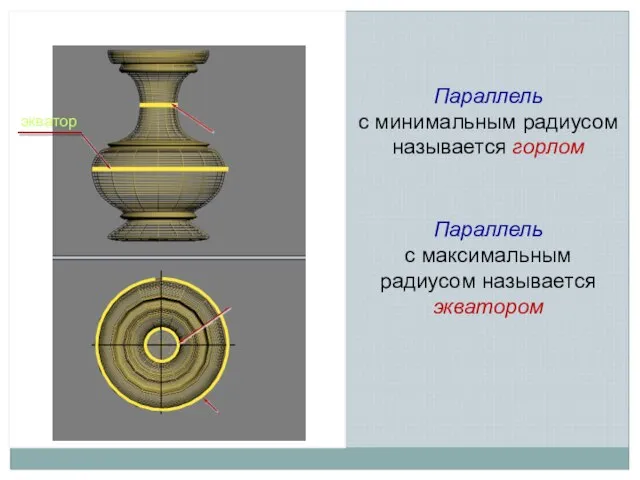
горло
горло
экватор
Параллель
с минимальным радиусом называется горлом
Параллель
с максимальным радиусом называется экватором
экватор

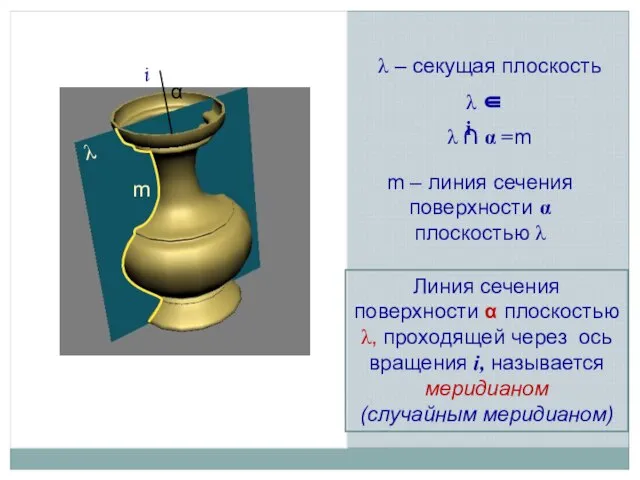
i
λ
α
λ – секущая плоскость
m – линия сечения поверхности α плоскостью λ
λ ∈ i
Линия сечения поверхности α плоскостью λ, проходящей через ось вращения i, называется меридианом
(случайным меридианом)
λ ∩ α =m
m

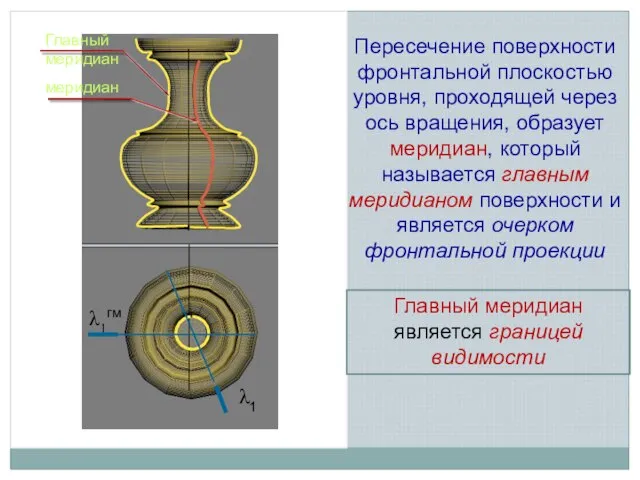
Главный меридиан
меридиан
λ1гм
Пересечение поверхности фронтальной плоскостью уровня, проходящей через ось вращения, образует меридиан, который называется главным меридианом поверхности и является очерком фронтальной проекции
Главный меридиан является границей видимости
λ1

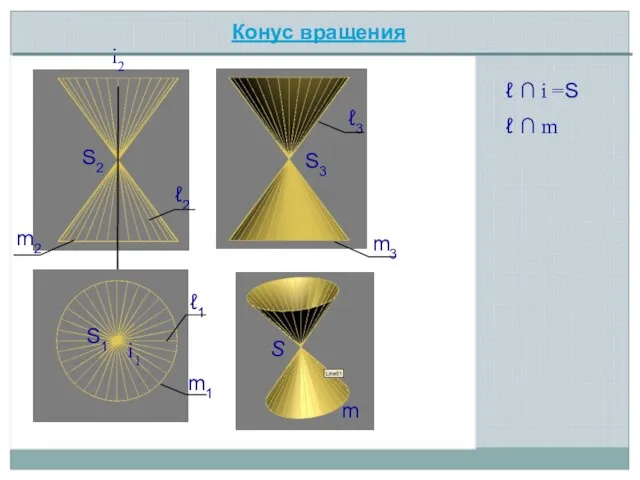
i2
S2
S
ℓ ∩ i =S
ℓ2
S1
S3
i1
ℓ1
m1
m2
ℓ ∩ m
m3
m
ℓ3
Конус вращения

Принадлежность точки поверхности

Точка принадлежит поверхности, если она принадлежит линии, расположенной на этой поверхности
Линия принадлежит поверхности, если каждая ее точка принадлежит этой поверхности

Среди точек кривой выделяют опорные точки:
– экстремальные точки – высшая и низшая, крайняя левая и крайняя правая, самая далекая и самая ближняя точки кривой;
– граничные точки видимости кривой, принадлежащей поверхности, лежат на очерках поверхности и отделяют видимую часть поверхности от ее невидимой части

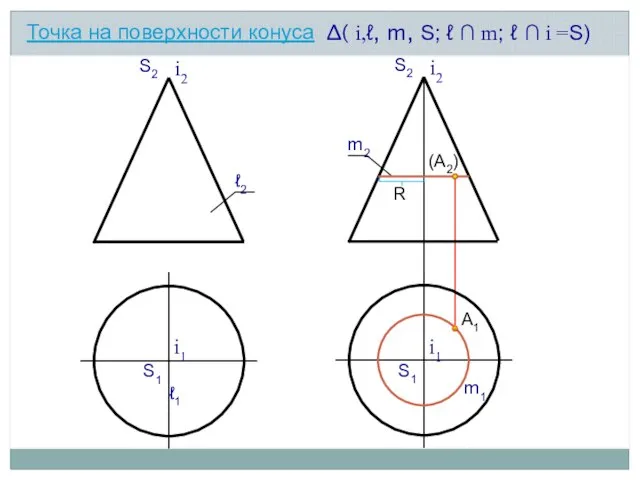
А2
А1
i2
S2
∆( i,ℓ, m, S; ℓ ∩ m; ℓ ∩ i =S)
ℓ2
S1
i1
ℓ1
(А2)
А1
i2
S2
m2
S1
i1
m1
Точка на поверхности конуса
R

Вогнутый тор (глобоид)
Поверхность, образованная внутренней стороной вращающейся дуги радиусом R, называется глобоидом

R
R
А2 ≡(В2 )
А1
А
В1

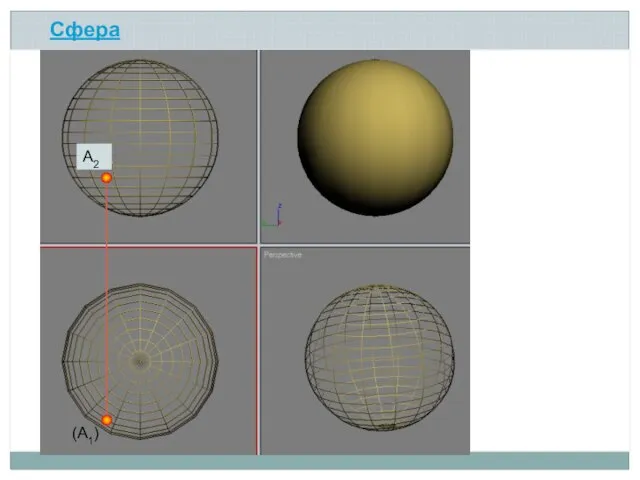
A2
(A1)
Сфера

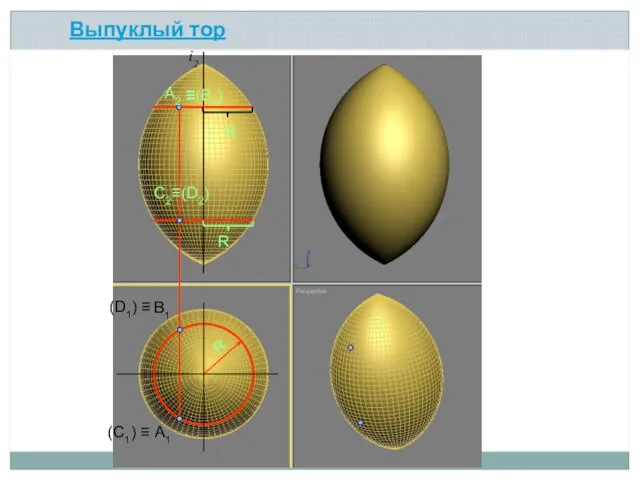
Выпуклый тор
R
R
А2
А1
R
В1
С2≡(D2)
(C1) ≡
(D1) ≡
≡(В2)
i2

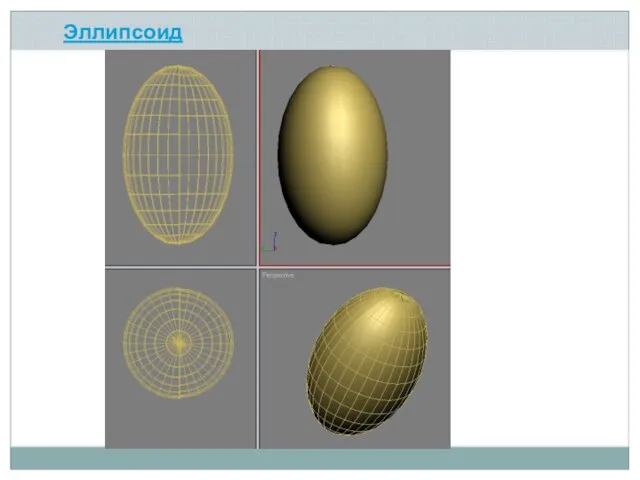
Эллипсоид

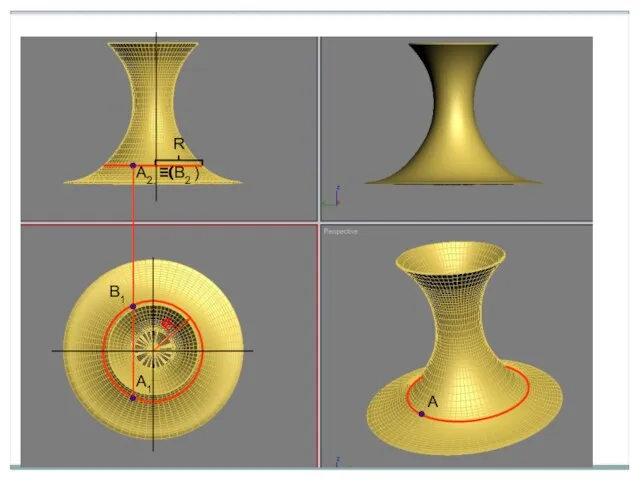
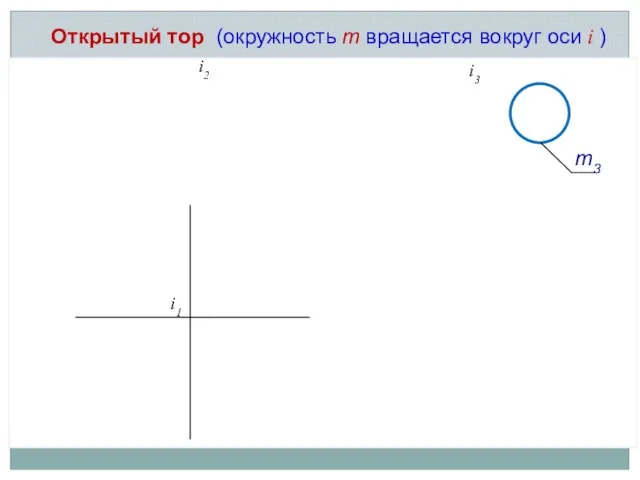
Открытый тор (окружность m вращается вокруг оси i )
i2
i1
i3
m3

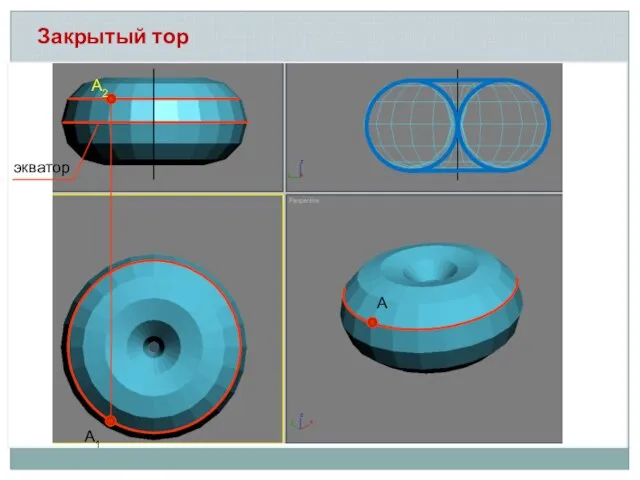
Закрытый тор
А2
А1
А
экватор

Закрытый кольцевой тор (самопересекающийся)