Содержание
- 2. Поверхность вращения Может быть построена в результате вращения двумерного объекта (прямая, плоская кривая) вокруг оси в
- 3. Вращение точки вокруг одной из координатных осей или произвольной прямой Результат построения – окружность
- 4. Отрезок и ось вращения компланарны и параллельны друг другу Результат построения – цилиндрическая поверхность или твердотельный
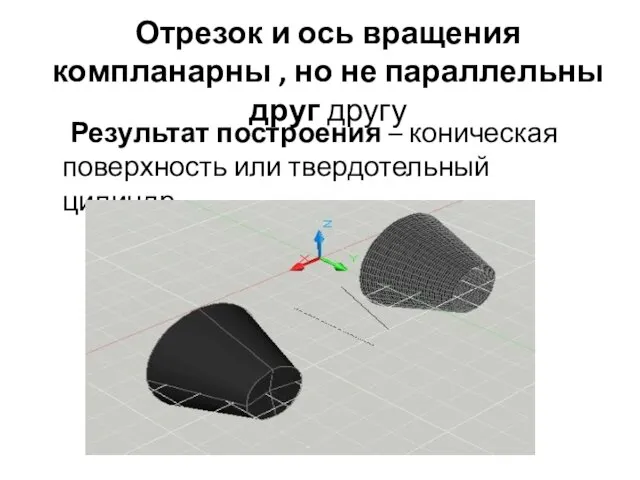
- 5. Отрезок и ось вращения компланарны , но не параллельны друг другу Результат построения – коническая поверхность
- 6. Отрезок и ось вращения компланарны, отрезок перпендикулярен оси вращения Результат построения: Плоский диск, если отрезок доходит
- 7. Отрезок и ось вращения не компланарны Результат построения - однополосный гиперболоид
- 8. Вращение половины окружности вокруг оси, лежащей в той же плоскости и проходящей через ее центр. Результат
- 9. Вращение половины эллипса вокруг оси, лежащей в той же плоскости и совпадающей с одной из его
- 10. Вращение окружности вокруг оси, лежащей с ней в одной плоскости и не пересекающей ее Результат построения
- 11. Математические основы построения поверхности вращения Поверхность вращения помимо самостоятельной трехмерной поверхностной модели может быть основой для
- 12. Рассмотрим математическое описание поверхности вращения вокруг оси X. Q(t,q)=[x(t), y(t)cos(q),y(t)sin(q)] Пояснения к данному выражению даны на
- 13. Данное математическое выражение поверхности вращения можно представить в матричном виде следующим образом.
- 15. Скачать презентацию









![Рассмотрим математическое описание поверхности вращения вокруг оси X. Q(t,q)=[x(t), y(t)cos(q),y(t)sin(q)] Пояснения к](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/402558/slide-11.jpg)

 Lluvia
Lluvia Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах
Жужжалочка. Дидактическая игра для автоматизации звука Ж в словах УД ПСИХОЛОГИЯ
УД ПСИХОЛОГИЯ Храмы России
Храмы России Оптическая микроскопия
Оптическая микроскопия Менеджмент
Менеджмент Кондитерский отдел
Кондитерский отдел Органы и службы стандартизации РФ
Органы и службы стандартизации РФ Вышел зайчик погулять Художник – В. Сергеев
Вышел зайчик погулять Художник – В. Сергеев Знакомство с точкой
Знакомство с точкой Состояние и задачи управления проектами в строительстве
Состояние и задачи управления проектами в строительстве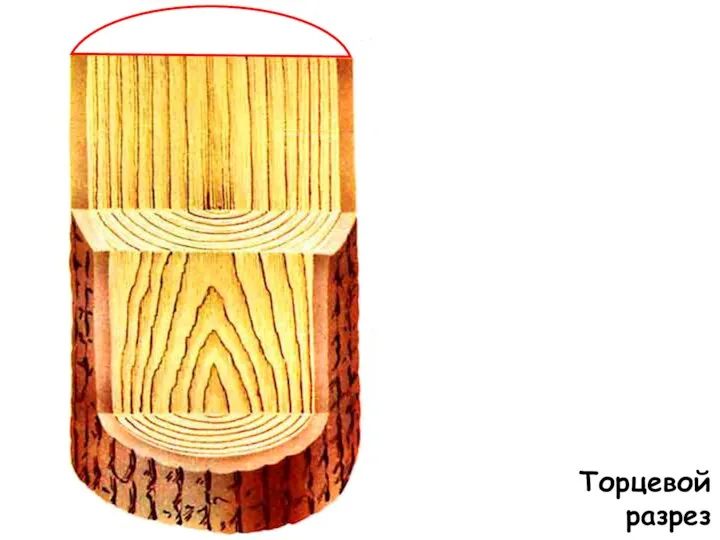 Торцевой разрез. Материаловедение
Торцевой разрез. Материаловедение чайные истории
чайные истории Шпаргалка юного покупателя
Шпаргалка юного покупателя Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор
Учебно-методический комплекс "Живая география" Живая география - учебно-методический комплекс, позволяющий использовать геоинфор Классификация реакций
Классификация реакций Организация хранения документов Архивного фонда Российской Федерации и других архивных документов
Организация хранения документов Архивного фонда Российской Федерации и других архивных документов Трансляция – биосинтез белка на рибосоме
Трансляция – биосинтез белка на рибосоме Инновационный подход к жизни
Инновационный подход к жизни DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D
DaCoPAn Software Engineering Project - Система динамической визуализации событий работы протоколов при обмене данными между двумя сетевыми ЭВМ — D Урок – размышление по рассказу К.Г. Паустовского «Телеграмма»
Урок – размышление по рассказу К.Г. Паустовского «Телеграмма» Путешествие в мир животных
Путешествие в мир животных СПАСИБО, АЗБУКА!
СПАСИБО, АЗБУКА! Rave Cosmology Today Dying, Death & Bardo . RC3.8
Rave Cosmology Today Dying, Death & Bardo . RC3.8 Основные закономерности развития информационного пространства
Основные закономерности развития информационного пространства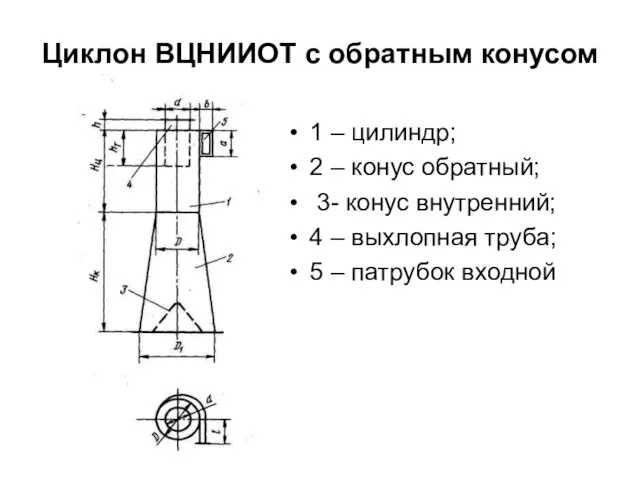 Циклон ВЦНИИОТ с обратным конусом
Циклон ВЦНИИОТ с обратным конусом  Квантовые компьютеры
Квантовые компьютеры Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)
Разработать рекламную кампанию в стиле шоу для молодежного интернет-издания Пи-Пермь (бюджет студенческой редакции)