Содержание
- 2. Задачи работы: Образовательные: обеспечить усвоение студентами геометрического содержания курса математики начальной школы Развивающие: развивать умение ясно
- 3. Заполни таблицу
- 4. - Проанализируем, что получилось? Каким образом распределён материал по классам? Какие учебники более насыщены геометрическим материалом?
- 5. - В каждой группе составьте кластер, где будут объединены понятия по выделенным нами группам. Кластер —
- 6. - Итак, мы убедились, какое большое количество геометрических понятий рассматривается в начальной школе. На следующем этапе
- 7. Текст для 1группы Линия — неопределяемое понятие. С линией знакомят, моделируя ее из шнура или рисуя
- 8. Текст для 2 группы Окружность и круг образованы замкнутой кривой линией. Круг — часть плоскости, ограниченная
- 9. Текст для 3 группы Замкнутая ломаная на плоскости ограничивает многоугольник. Треугольник ограничен ломаной из трех звеньев.
- 10. Текст для 4 группы Точка – неопределяемое понятие. С точкой обычно знакомят, рисуя её или прокалывая
- 12. Скачать презентацию
Слайд 2Задачи работы:
Образовательные: обеспечить усвоение студентами геометрического содержания курса математики начальной школы
Развивающие: развивать
Задачи работы:
Образовательные: обеспечить усвоение студентами геометрического содержания курса математики начальной школы
Развивающие: развивать

умение ясно выражать свои мысли, анализировать, сравнивать, делать выводы и обобщения, развивать грамотную математическую речь
Воспитательные: создать условия для воспитания навыков сотрудничества, умения слушать и работать в группах, умения анализировать свою деятельность и деятельность своих товарищей, формировать способности в принятии совместного решения.
Воспитательные: создать условия для воспитания навыков сотрудничества, умения слушать и работать в группах, умения анализировать свою деятельность и деятельность своих товарищей, формировать способности в принятии совместного решения.
Слайд 3Заполни таблицу
Заполни таблицу
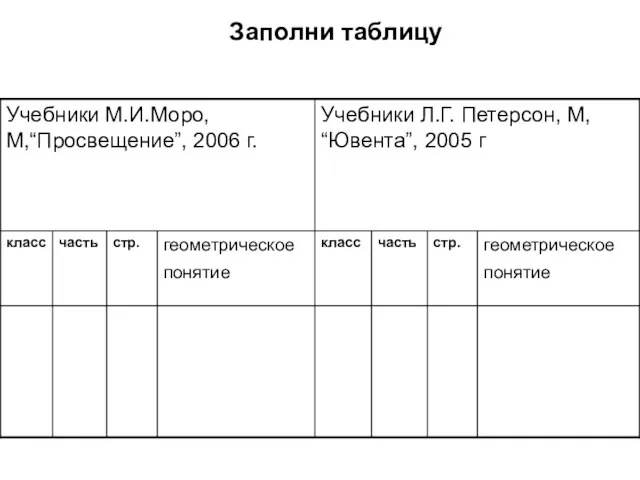
Слайд 4- Проанализируем, что получилось? Каким образом распределён материал по классам? Какие учебники
- Проанализируем, что получилось? Каким образом распределён материал по классам? Какие учебники

более насыщены геометрическим материалом?
- На какие большие группы можно разделить весь геометрический материал в начальной школе, с какими основными геометрическими понятиями знакомятся младшие школьники в период обучения?
Линии-1группа.
Окружность и круг-2группа.
Многоугольники-3группа.
Точка, числовой луч-4группа.
Углы-5группа.
- На какие большие группы можно разделить весь геометрический материал в начальной школе, с какими основными геометрическими понятиями знакомятся младшие школьники в период обучения?
Линии-1группа.
Окружность и круг-2группа.
Многоугольники-3группа.
Точка, числовой луч-4группа.
Углы-5группа.
Слайд 5- В каждой группе составьте кластер, где будут объединены понятия по выделенным
- В каждой группе составьте кластер, где будут объединены понятия по выделенным

нами группам.
Кластер — это объединение в систему однородных единиц. При этом данная система может считаться самостоятельным элементом обладающим определёнными свойствами.
Кластер — это объединение в систему однородных единиц. При этом данная система может считаться самостоятельным элементом обладающим определёнными свойствами.
Слайд 6- Итак, мы убедились, какое большое количество геометрических понятий рассматривается в начальной
- Итак, мы убедились, какое большое количество геометрических понятий рассматривается в начальной

школе. На следующем этапе нашего занятия мы постараемся все эти понятия восстановить в своей памяти. Для этого используем режим работы “Зигзаг”.
Слайд 7Текст для 1группы
Линия — неопределяемое понятие. С линией знакомят, моделируя ее из
Текст для 1группы
Линия — неопределяемое понятие. С линией знакомят, моделируя ее из

шнура или рисуя на доске, на листе бумаги.
Прямую линию удобно демонстрировать, согнув любой лист бумаги — линия сгиба всегда прямая. Основное свойство прямой линии: прямая линия бесконечна.
Кривую линию удобно моделировать из шнура. Кривые могут быть замкнутыми и незамкнутыми.
В программе 1 класса рассматривают только линии на плоскости.
Основные взаимоотношения точки и прямой (или кривой) линии, с которыми знакомятся дети в 1 классе:
• Через одну точку можно провести множество прямых.
• Через одну точку можно провести множество кривых.,
• Через две точки можно провести только одну прямую.
• Через две точки можно провести множество кривых.
Ломаную линию удобно моделировать, используя счетные палочки или складной металлический метр.
Отрезок прямой-множество, состоящее из двух различных точек и всех точек, лежащих между ними.
Ломаная— обединение отрезков, конец каждого из которых(кроме последнего) является началом следующего и смежные отрезки не лежат на одной прямой.
Звено ломаной — отрезок. Точки соединения концов звеньев называют вершинами ломаной.
Ломаная (как и кривая линия) может быть замкнутой и незамкнутой. На рисунке выше ломаная 1 — незамкнутая, ломаная, 3 — замкнутая.
Длина ломаной — сумма длин звеньев ломаной. Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.
Прямую линию удобно демонстрировать, согнув любой лист бумаги — линия сгиба всегда прямая. Основное свойство прямой линии: прямая линия бесконечна.
Кривую линию удобно моделировать из шнура. Кривые могут быть замкнутыми и незамкнутыми.
В программе 1 класса рассматривают только линии на плоскости.
Основные взаимоотношения точки и прямой (или кривой) линии, с которыми знакомятся дети в 1 классе:
• Через одну точку можно провести множество прямых.
• Через одну точку можно провести множество кривых.,
• Через две точки можно провести только одну прямую.
• Через две точки можно провести множество кривых.
Ломаную линию удобно моделировать, используя счетные палочки или складной металлический метр.
Отрезок прямой-множество, состоящее из двух различных точек и всех точек, лежащих между ними.
Ломаная— обединение отрезков, конец каждого из которых(кроме последнего) является началом следующего и смежные отрезки не лежат на одной прямой.
Звено ломаной — отрезок. Точки соединения концов звеньев называют вершинами ломаной.
Ломаная (как и кривая линия) может быть замкнутой и незамкнутой. На рисунке выше ломаная 1 — незамкнутая, ломаная, 3 — замкнутая.
Длина ломаной — сумма длин звеньев ломаной. Для нахождения длины ломаной следует измерить длину каждого звена и результаты сложить.
Слайд 8Текст для 2 группы
Окружность и круг образованы замкнутой кривой линией.
Круг — часть
Текст для 2 группы
Окружность и круг образованы замкнутой кривой линией.
Круг — часть

плоскости, ограниченная окружностью.
Окружность-множество точек плоскости , находящихся на данном расстоянии от данной точки, лежащей в этой же плоскости.
Поскольку в начальных классах не дается классическое определение окружности, то знакомство с окружностью проводят методом показа, связывая его с непосредственной практической деятельностью по вычерчиванию окружности с помощью циркуля.
Замкнутая кривая линия, которую рисует грифель циркуля, — это окружность.
Окружность (круг) имеет центр. Точка О — центр окружности (круга).
Радиус — отрезок, соединяющий центр окружности с какой-нибудь ее точкой.
Например: ОМ— радиус окружности (круга).
Радиусы одной окружности (круга) равны.
Диаметр — отрезок, проходящий через центр окружности (круга) и соединяющий две любые ее точки.
Например: диаметр АD.
Основное свойство диаметров одной окружности (круга).
Диаметры одной окружности (круга) равны. Диаметр равен двум радиусам.
Окружность-множество точек плоскости , находящихся на данном расстоянии от данной точки, лежащей в этой же плоскости.
Поскольку в начальных классах не дается классическое определение окружности, то знакомство с окружностью проводят методом показа, связывая его с непосредственной практической деятельностью по вычерчиванию окружности с помощью циркуля.
Замкнутая кривая линия, которую рисует грифель циркуля, — это окружность.
Окружность (круг) имеет центр. Точка О — центр окружности (круга).
Радиус — отрезок, соединяющий центр окружности с какой-нибудь ее точкой.
Например: ОМ— радиус окружности (круга).
Радиусы одной окружности (круга) равны.
Диаметр — отрезок, проходящий через центр окружности (круга) и соединяющий две любые ее точки.
Например: диаметр АD.
Основное свойство диаметров одной окружности (круга).
Диаметры одной окружности (круга) равны. Диаметр равен двум радиусам.
Слайд 9Текст для 3 группы
Замкнутая ломаная на плоскости ограничивает многоугольник. Треугольник ограничен ломаной
Текст для 3 группы
Замкнутая ломаная на плоскости ограничивает многоугольник. Треугольник ограничен ломаной

из трех звеньев. Звенья называют сторонами, а их общие точки вершинами. У треугольника три стороны и три вершины.
Треугольники, имеющие стороны разной длины, называют разносторонними.
Треугольники, у которых равны две стороны, называют равнобедренными.
Среди равнобедренных треугольников есть такие, у которых равны все три стороны. Эти треугольники называют равносторонними.
Остроугольным называется треугольник, все углы которого острые.
Прямоугольным называется треугольник, который имеет прямой угол.
Тупоугольным называется треугольник, который имеет тупой угол.
Четырехугольник ограничен ломаной из четырех звеньев. Четырехугольник имеет четыре стороны и четыре вершины.
Прямой угол — это угол, который по определению содержит 90 градусов. Прямоугольник — четырехугольник, у которого все углы прямые.
Основное свойство прямоугольника: противолежащие стороны прямоугольника имеют равные длины.
Модель прямого угла служит средством проверки выбора прямоугольников. В дальнейшем бумажная модель прямого угла заменяется на угольник, который является основным инструментом для распознавания и построения прямых углов.
Основное свойство прямоугольника дети определяют опытным путем: перегибают бумажные модели прямоугольников, совмещая противолежащие стороны.
Квадрат - прямоугольник, у которого все стороны равны.
Диагональ — отрезок, соединяющий противолежащие вершины многоугольника.
Диагонали квадрата пересекаются под прямым углом. Диагонали прямоугольника имеют равные длины. Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.
С диагоналями прямоугольника детей знакомят методом показа:
Отрезки АВ и СD диагонали прямоугольника АВСD. Точка Е — точка пересечения диагоналей. Свойства диагоналей прямоугольника определяются эмпирическим (опытным) путем — измерением длин соответствующих отрезков.
Поскольку квадрат является прямоугольником, то его диагонали обладают теми же свойствами.
Периметр многоугольника — сумма длин всех его сторон.
Для нахождения периметра многоугольника измеряют длины его сторон и складывают полученные результаты.
Площадь плоской фигуры измеряется количеством стандартных мер площади, укладывающихся внутри фигуры.
Дети знакомятся с единицей измерения 1 см2.
Инструмент для определения площади всех фигур — палетка.
Палетка — лист кальки (или прозрачного пластика), на который нанесена сетка квадратов размером 1х1 см.
Чтобы вычислить площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
Треугольники, имеющие стороны разной длины, называют разносторонними.
Треугольники, у которых равны две стороны, называют равнобедренными.
Среди равнобедренных треугольников есть такие, у которых равны все три стороны. Эти треугольники называют равносторонними.
Остроугольным называется треугольник, все углы которого острые.
Прямоугольным называется треугольник, который имеет прямой угол.
Тупоугольным называется треугольник, который имеет тупой угол.
Четырехугольник ограничен ломаной из четырех звеньев. Четырехугольник имеет четыре стороны и четыре вершины.
Прямой угол — это угол, который по определению содержит 90 градусов. Прямоугольник — четырехугольник, у которого все углы прямые.
Основное свойство прямоугольника: противолежащие стороны прямоугольника имеют равные длины.
Модель прямого угла служит средством проверки выбора прямоугольников. В дальнейшем бумажная модель прямого угла заменяется на угольник, который является основным инструментом для распознавания и построения прямых углов.
Основное свойство прямоугольника дети определяют опытным путем: перегибают бумажные модели прямоугольников, совмещая противолежащие стороны.
Квадрат - прямоугольник, у которого все стороны равны.
Диагональ — отрезок, соединяющий противолежащие вершины многоугольника.
Диагонали квадрата пересекаются под прямым углом. Диагонали прямоугольника имеют равные длины. Отрезки, получаемые при пересечении диагоналей прямоугольника, равны.
С диагоналями прямоугольника детей знакомят методом показа:
Отрезки АВ и СD диагонали прямоугольника АВСD. Точка Е — точка пересечения диагоналей. Свойства диагоналей прямоугольника определяются эмпирическим (опытным) путем — измерением длин соответствующих отрезков.
Поскольку квадрат является прямоугольником, то его диагонали обладают теми же свойствами.
Периметр многоугольника — сумма длин всех его сторон.
Для нахождения периметра многоугольника измеряют длины его сторон и складывают полученные результаты.
Площадь плоской фигуры измеряется количеством стандартных мер площади, укладывающихся внутри фигуры.
Дети знакомятся с единицей измерения 1 см2.
Инструмент для определения площади всех фигур — палетка.
Палетка — лист кальки (или прозрачного пластика), на который нанесена сетка квадратов размером 1х1 см.
Чтобы вычислить площадь прямоугольника, измеряют его длину и ширину (в одинаковых единицах) и находят произведение полученных чисел.
Слайд 10Текст для 4 группы
Точка – неопределяемое понятие. С точкой обычно знакомят, рисуя
Текст для 4 группы
Точка – неопределяемое понятие. С точкой обычно знакомят, рисуя

её или прокалывая стержнем ручки в листочке бумаги. Считается, что точка не имеет ни длины, ни ширины, ни площади.
Луч — часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
Точка А— начало луча.
В математике луч обычно обозначается двумя буквами, например: луч АС. Такая запись обозначает, что луч имеет началом точку А и “идет” в сторону, обозначенную буквой С:
Числовой луч — луч, на котором точками обозначены натуральные числа. Расстояние между точками равно 1 единице измерения (единичный отрезок), которая задается условно.
Каждой точке ставится в соответствие число, начиная с числа 1. Началу луча ставится в соответствие число О.
Числовой луч играет большую роль при иллюстрации понятия “натуральный ряд чисел”, позволяет сравнивать натуральные числа, ориентируясь на их расположение на числовом луче, позволяет выполнять приемы присчитывания и отсчитывания по частям с опорой на числовой луч. Другая роль числового луча состоит в том, что, используя это понятие, можно познакомить детей с прямоугольной системой координат (числовой или координатный угол), отрицательными числами (числовая прямая).
Луч — часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
Точка А— начало луча.
В математике луч обычно обозначается двумя буквами, например: луч АС. Такая запись обозначает, что луч имеет началом точку А и “идет” в сторону, обозначенную буквой С:
Числовой луч — луч, на котором точками обозначены натуральные числа. Расстояние между точками равно 1 единице измерения (единичный отрезок), которая задается условно.
Каждой точке ставится в соответствие число, начиная с числа 1. Началу луча ставится в соответствие число О.
Числовой луч играет большую роль при иллюстрации понятия “натуральный ряд чисел”, позволяет сравнивать натуральные числа, ориентируясь на их расположение на числовом луче, позволяет выполнять приемы присчитывания и отсчитывания по частям с опорой на числовой луч. Другая роль числового луча состоит в том, что, используя это понятие, можно познакомить детей с прямоугольной системой координат (числовой или координатный угол), отрицательными числами (числовая прямая).
 Отмена ЕНВД
Отмена ЕНВД Рынок земли(природных ресурсов)
Рынок земли(природных ресурсов) «Электричество и растения».
«Электричество и растения». Роль женщины-матери в духовно-нравственном воспитании детей
Роль женщины-матери в духовно-нравственном воспитании детей Риск-менеджмент. Теоретические основы рискологии. Лекция №1
Риск-менеджмент. Теоретические основы рискологии. Лекция №1 Моя любимая игра: ,,Страйкбол”
Моя любимая игра: ,,Страйкбол” Что такое Recognition? Программа Recognition (перевод с англ. признание) – это инновационный продукт на международном образовательном рынке.
Что такое Recognition? Программа Recognition (перевод с англ. признание) – это инновационный продукт на международном образовательном рынке.  Презентация на тему Петр I
Презентация на тему Петр I  Единое и расчлененное знание в истории культуры
Единое и расчлененное знание в истории культуры 2_5390911506760081685
2_5390911506760081685 Государственный Фонд развития промышленности Рязанской области (ГФРП РО)
Государственный Фонд развития промышленности Рязанской области (ГФРП РО) Некоторые задачи планирования сети магистрального оператора
Некоторые задачи планирования сети магистрального оператора Жизнь и творчество Л.Н. Толстого (1828-1910)
Жизнь и творчество Л.Н. Толстого (1828-1910) Трансплантация
Трансплантация Разработка продающего сайта
Разработка продающего сайта Литература и искусство эпохи Возрождения
Литература и искусство эпохи Возрождения Слайд только для инструкторов *** Не демонстрировать во время презентации
Слайд только для инструкторов *** Не демонстрировать во время презентации МОУ МАГАНСКАЯ СОШ
МОУ МАГАНСКАЯ СОШ Эко-отель Leaprus
Эко-отель Leaprus Презентация на тему Три состояния вещества Физика 7 класс
Презентация на тему Три состояния вещества Физика 7 класс  Клеточное строение корня (1)
Клеточное строение корня (1) Административные дела (первая инстанция) Урок 3.2. Рассмотрение административного дела
Административные дела (первая инстанция) Урок 3.2. Рассмотрение административного дела Зразы картофельные с грибами (замороженный полуфабрикат)
Зразы картофельные с грибами (замороженный полуфабрикат) Внедрение ГШИС и КМИС КУ в образовательном учреждении
Внедрение ГШИС и КМИС КУ в образовательном учреждении Правописание суффиксов -чик- и -щик-
Правописание суффиксов -чик- и -щик- Тест "Про кошек и собак" 2 класс
Тест "Про кошек и собак" 2 класс Смертная казнь по законодательству Республики Казахстан: история и современность
Смертная казнь по законодательству Республики Казахстан: история и современность Первый питательный крем от Anew - Ультра-Питание
Первый питательный крем от Anew - Ультра-Питание