Содержание
- 2. Цель проекта: Познакомиться с правильными многогранниками. Изучить их формы и узнать где они встречаются. Исследовать практическое
- 3. ЗАДАЧИ: Развивать эстетическое восприятие математический фактов, расширить представление о сфере применения математики. Расширить кругозор посредством знакомства
- 4. МЕТОДЫ: Работа с литературой. Работа с интернет-ресурсами. Беседа с преподавателем математики. Наблюдение.
- 5. Виды многогранников Многогранник- это поверхность составленная из многоугольников, а также тело ограниченное такой поверхностью.
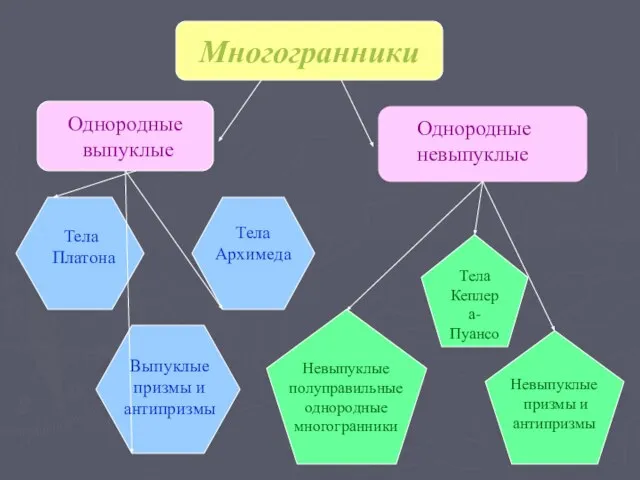
- 6. Многогранники Однородные выпуклые Однородные невыпуклые Тела Архимеда Тела Платона Выпуклые призмы и антипризмы Тела Кеплера- Пуансо
- 7. Правильными многогранниками называют выпуклые многогранники, все грани и все углы которых равны, причем грани - правильные
- 8. Существует лишь пять выпуклых правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными гранями, куб (гексаэдр)
- 9. огонь тетраэдр икосаэдр октаэдр гексаэдр вселенная додекаэдр вода земля воздух Платон предположил, что атомы четырех «основных
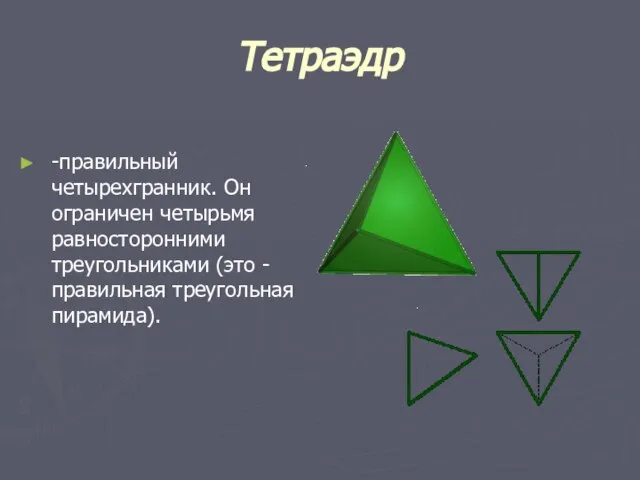
- 10. Тетраэдр -правильный четырехгранник. Он ограничен четырьмя равносторонними треугольниками (это - правильная треугольная пирамида).
- 11. Гексаэдр - правильный шестигранник. Это куб состоящий из шести равных квадратов.
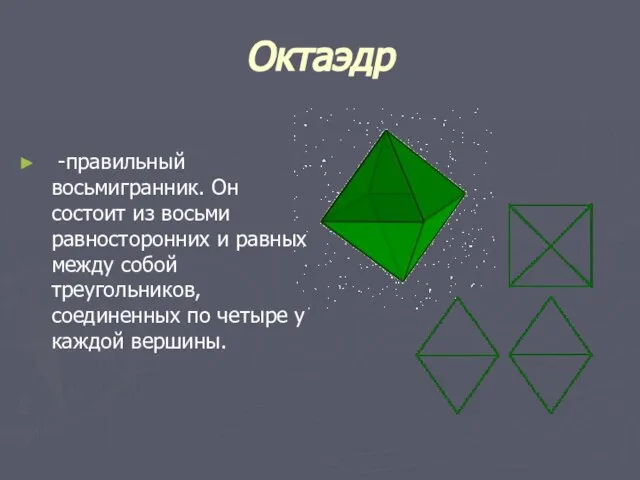
- 12. Октаэдр -правильный восьмигранник. Он состоит из восьми равносторонних и равных между собой треугольников, соединенных по четыре
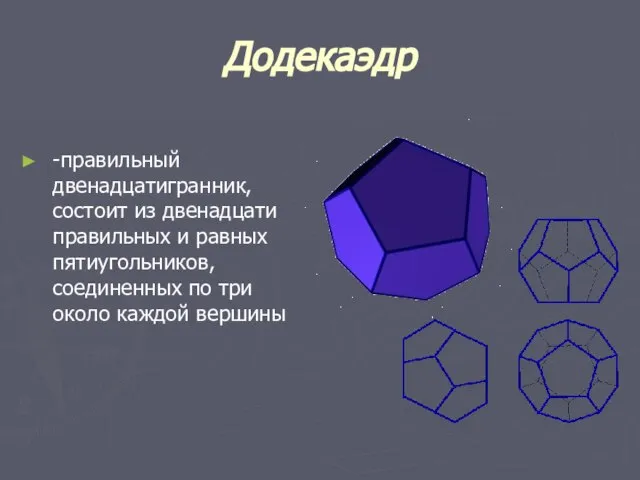
- 13. Додекаэдр -правильный двенадцатигранник, состоит из двенадцати правильных и равных пятиугольников, соединенных по три около каждой вершины
- 14. Икосаэдр -состоит из 20 равносторонних и равных треугольников, соединенных по пять около каждой вершины
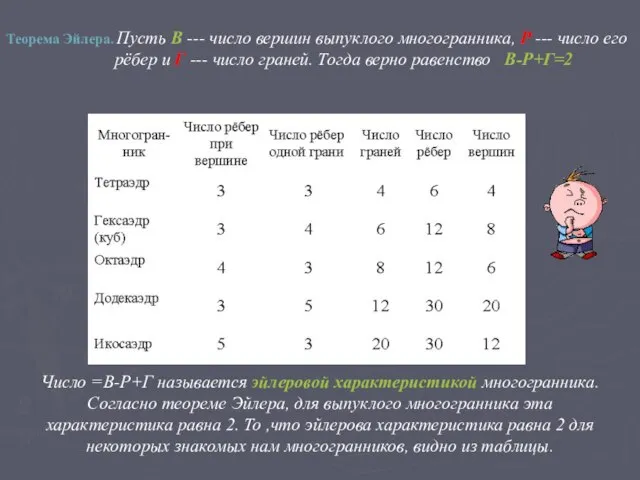
- 15. Число =В-Р+Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2.
- 16. Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется. Кристаллы — эти твёрдые тела
- 17. Молекула МЕТАНА имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями молекулы метана, полученными при помощи электронного
- 18. Кристаллы поваренной соли имеют форму куба, кристаллы льда и горного хрусталя (кварца) напоминают отточенный с двух
- 19. Форму одноклеточных организмов – феодарий точно передает икосаэдр. Чем же вызвана такая природная геометризация? Может быть,
- 20. Пятничный многогранник: “огуречный” вирус На картинке – вирус, поражающий ценные растения типа помидоров и огурцов. Именно
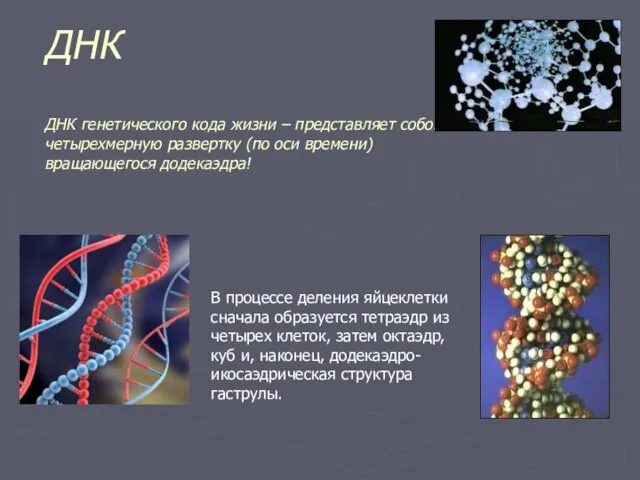
- 21. ДНК ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра! В
- 22. Искусство впрочем, многогранники - отнюдь не только объект научных исследований. Их формы - завершенные и причудливые,
- 23. Так как правильные многогранники обладают жесткостью, то каркасы куполов церквей делают в виде правильных многогранников Многогранники
- 25. Скачать презентацию
















 (–1) · 3 =
(–1) · 3 = Осмотр общего имущества в многоквартирном доме
Осмотр общего имущества в многоквартирном доме EV3 Самосвал
EV3 Самосвал Инвестиционный фонд МАП «Инновационный лифт»
Инвестиционный фонд МАП «Инновационный лифт» Нам нужны союзники!
Нам нужны союзники! Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3
Дисциплина: Международные перевозки грузов РАЗДЕЛ 3. Обеспечивающий комплекс организации международной перевозки грузов Тема 3 Мое зазеркалье
Мое зазеркалье Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем
Московский колледж бизнес-технологий. Эксплуатация беспилотных авиационных систем Презентация Microsoft PowerPoint (3)
Презентация Microsoft PowerPoint (3) Презентация на тему Иудаизм презентация 4 класс
Презентация на тему Иудаизм презентация 4 класс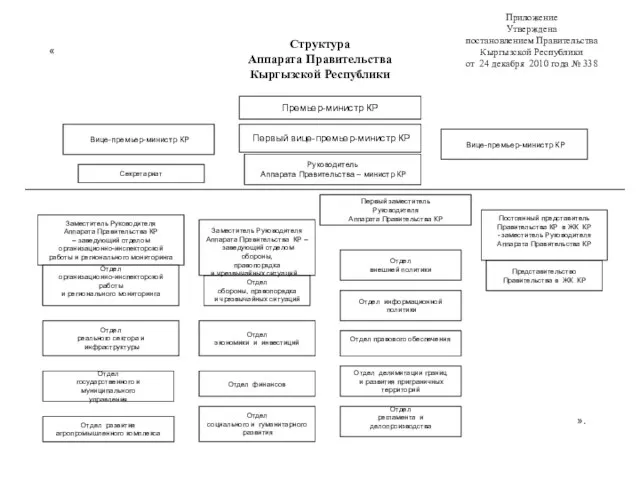 Структура Аппарата Правительства Кыргызской Республики
Структура Аппарата Правительства Кыргызской Республики Автоматизированная информационная система «Государственный заказ»
Автоматизированная информационная система «Государственный заказ» Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов
Формирование экологической культуры обучающихся колледжа через реализацию социально-образовательых проектов Тема урока «Право на труд. Трудовые правоотношения»
Тема урока «Право на труд. Трудовые правоотношения» Класс 1-1 3주 후 시험문제 읽기 Чтение
Класс 1-1 3주 후 시험문제 읽기 Чтение Обобщающий урок - игра по теме: «Я знаю край родной».
Обобщающий урок - игра по теме: «Я знаю край родной». Тяжелая атлетика в России и за рубежом
Тяжелая атлетика в России и за рубежом Разработка мероприятия Цифровой текстиль. Синтетические ткани
Разработка мероприятия Цифровой текстиль. Синтетические ткани Лекция_6 ЭТД ФТД.ppt
Лекция_6 ЭТД ФТД.ppt Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс
Презентация на тему Сочинение по картине Левитана «Весна. Большая вода» 4 класс Методы мониторинга репутациив социальных медиа
Методы мониторинга репутациив социальных медиа Областной конкурспервичных профсоюзныхорганизаций.
Областной конкурспервичных профсоюзныхорганизаций. Контроль квалификации сварщиков. Система аттестации сварочного производства
Контроль квалификации сварщиков. Система аттестации сварочного производства Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1)
Уголовное законодательство Республики Казахстан на страже воинского правопорядка (занятие 1) 36736
36736 Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс)
Презентация на тему Разгром империи Наполеона. Венский конгресс (8 класс) Электрическая лампа накаливания
Электрическая лампа накаливания 20161206_avstraliya-i-okeaniya
20161206_avstraliya-i-okeaniya