Презентация на тему Четырехугольники 8 класс

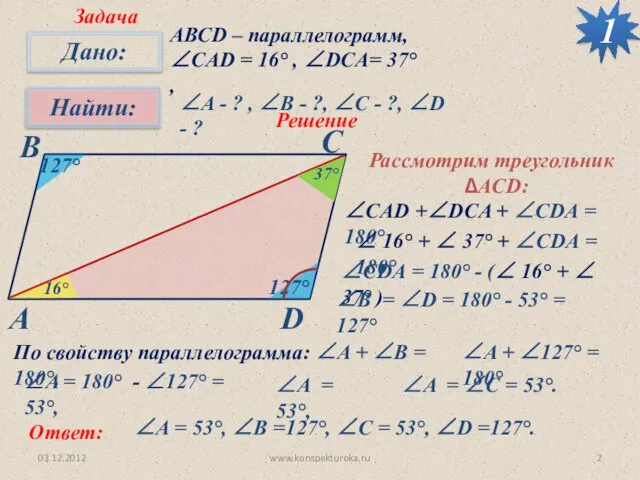
03.12.2012
www.konspekturoka.ru
1
АВСD – параллелограмм,
∠CAD = 16° , ∠DCA= 37° ,
∠A - ? , ∠B - ?, ∠C - ?, ∠D - ?
Задача
Решение
Рассмотрим треугольник
∆ACD:
∠CAD +∠DCA + ∠СDА = 180°
∠ 16° + ∠ 37° + ∠СDА = 180°
∠СDА = 180° - (∠ 16° + ∠ 37° )
∠B = ∠D = 180° - 53° = 127°
По свойству параллелограмма: ∠A + ∠B = 180°,
∠A + ∠127° = 180°
∠A = 180° - ∠127° = 53°,
∠A = 53°,
∠A = ∠C = 53°.
Ответ:
∠A = 53°, ∠B =127°, ∠C = 53°, ∠D =127°.

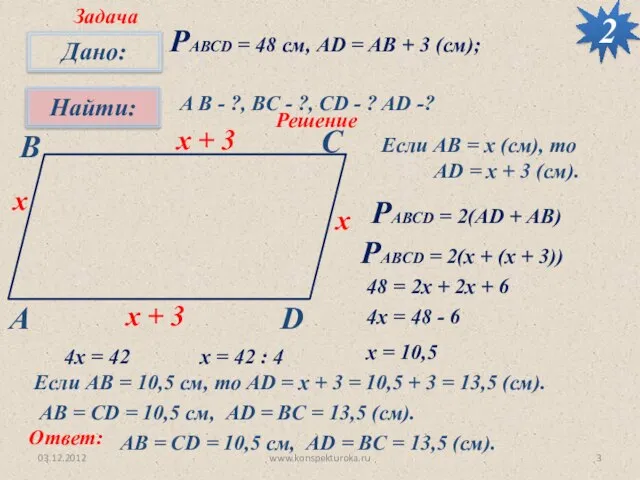
03.12.2012
www.konspekturoka.ru
2
РАВСD = 48 см, AD = AB + 3 (см);
A B - ?, ВC - ?, CD - ? AD -?
Задача
Ответ:
Решение
х
х
х + 3
х + 3
Если АВ = х (см), то
AD = x + 3 (см).
РАВСD = 2(AD + AB)
РАВСD = 2(x + (x + 3))
48 = 2x + 2x + 6
4x = 48 - 6
4x = 42
x = 42 : 4
x = 10,5
Если АВ = 10,5 см, то AD = x + 3 = 10,5 + 3 = 13,5 (см).
АВ = CD = 10,5 см, AD = BC = 13,5 (см).
АВ = CD = 10,5 см, AD = BC = 13,5 (см).

03.12.2012
www.konspekturoka.ru
3
РАВСD = 48 см, AD - AB = 7 (см);
A B - ?, ВC - ?, CD - ? AD -?
Задача
Ответ:
Решение
х
х
х + 7
х + 7
Если АВ = х (см), то
AD = x + 7 (см).
РАВСD = 2(AD + AB)
РАВСD = 2(x + (x + 7))
48 = 2x + 2x + 14
4x = 48 - 14
4x = 34
x = 34 : 4
x = 8,5
Если АВ = 8,5 см, то AD = x + 7 = 8,5 + 7 = 15,5 (см).
АВ = CD = 8,5 см, AD = BC = 15,5 (см).
АВ = CD = 8,5 см, AD = BC = 15,5 (см).

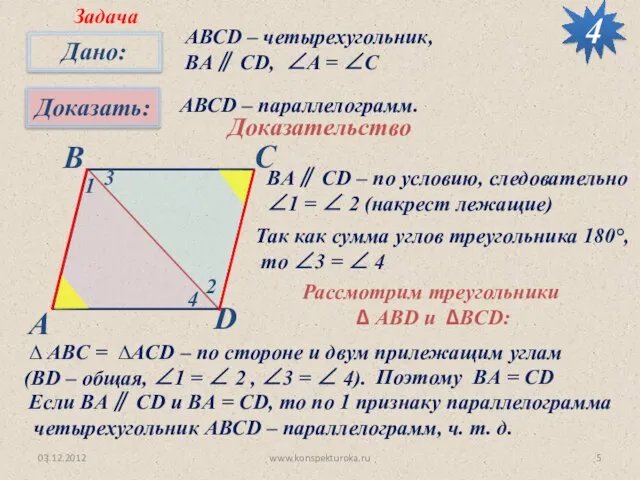
03.12.2012
www.konspekturoka.ru
4
АВСD – четырехугольник,
BА∥ CD, ∠A = ∠C
АВСD – параллелограмм.
Доказательство
Задача
1
2
3
4
BА∥ CD – по условию, следовательно
∠1 = ∠ 2 (накрест лежащие)
Рассмотрим треугольники
∆ АBD и ∆BCD:
Так как сумма углов треугольника 180°,
то ∠3 = ∠ 4
∆ АBC = ∆ACD – по стороне и двум прилежащим углам
(ВD – общая, ∠1 = ∠ 2 , ∠3 = ∠ 4).
Поэтому BА = CD
Если BА∥ CD и BА = CD, то по 1 признаку параллелограмма
четырехугольник АВСD – параллелограмм, ч. т. д.

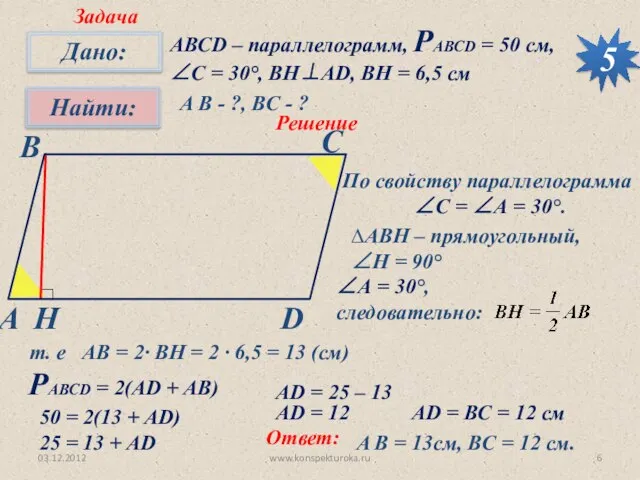
03.12.2012
www.konspekturoka.ru
5
Задача
АВСD – параллелограмм, РАВСD = 50 см,
∠С = 30°, BH⊥AD, BH = 6,5 см
A B - ?, ВC - ?
Решение
Н
∟
По свойству параллелограмма
∠С = ∠А = 30°.
∆АВН – прямоугольный,
∠Н = 90°
∠А = 30°,
следовательно:
т. е АВ = 2· ВН = 2 · 6,5 = 13 (см)
РАВСD = 2(AD + AB)
50 = 2(13 + AD)
25 = 13 + AD
AD = 25 – 13
AD = 12
Ответ:
A B = 13см, ВC = 12 см.
AD = ВС = 12 см

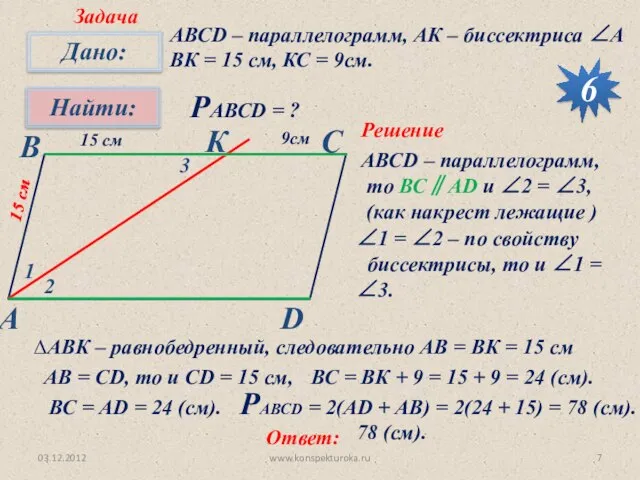
03.12.2012
www.konspekturoka.ru
Задача
6
АВСD – параллелограмм, АК – биссектриса ∠А
ВК = 15 см, КС = 9см.
РАВСD = ?
1
2
3
Решение
АВСD – параллелограмм,
то ВС∥AD и ∠2 = ∠3,
(как накрест лежащие )
∠1 = ∠2 – по свойству
биссектрисы, то и ∠1 = ∠3.
К
∆АВК – равнобедренный, следовательно АВ = ВК = 15 см
15 см
9см
АВ = СD, то и СD = 15 см,
ВС = ВК + 9 = 15 + 9 = 24 (см).
15 см
ВС = AD = 24 (см).
РАВСD = 2(AD + AB) = 2(24 + 15) = 78 (cм).
Ответ:
78 (cм).