произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рm,n того, что в результате n испытаний событие А наступило ровно m раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
8
Повторение испытаний.
Формула Бернулли










 Сервис Мечты
Сервис Мечты Основи формування і реєстраціi корисного сигналу в діапазоні
Основи формування і реєстраціi корисного сигналу в діапазоні Комплексная система автоматизации
Комплексная система автоматизации Телепорт
Телепорт Осторожно! Сосульки
Осторожно! Сосульки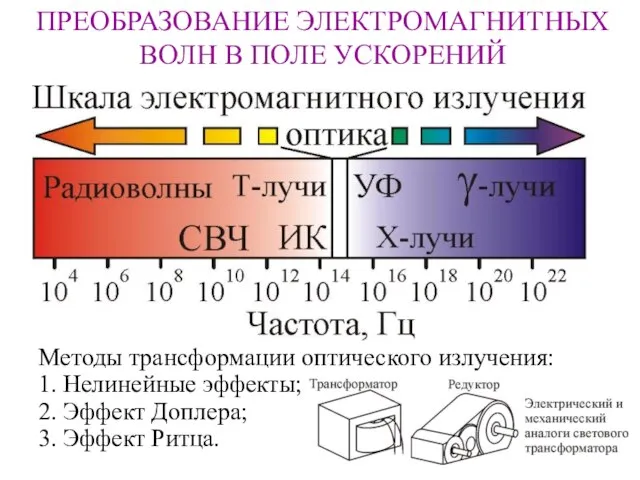 ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ
ПРЕОБРАЗОВАНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ПОЛЕ УСКОРЕНИЙ Примеры комбинаторных задач (9 класс)
Примеры комбинаторных задач (9 класс) Решение логических задач из курса кибернетики
Решение логических задач из курса кибернетики Бедность
Бедность Nocturnal eczema: Review of sleep and circadian rhythms
Nocturnal eczema: Review of sleep and circadian rhythms Microsoft Office Word 2007
Microsoft Office Word 2007 Международное сотрудничество в освоении космического пространства
Международное сотрудничество в освоении космического пространства Золото
Золото Презентация на тему Загадки о диких животных
Презентация на тему Загадки о диких животных Королева оркестра
Королева оркестра Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина
Экологическое просвещение в творчествеВладимира Алексеевича Чивилихина Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар
Ҳозирги замон ҳуқуқи ва унинг моҳияти ҳақидаги концепциялар Образ Чичикова в поэме "Мертвые души"
Образ Чичикова в поэме "Мертвые души" Табір "Світанок"
Табір "Світанок" Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана Онтология
Онтология  Источники загрязнения окружающей среды
Источники загрязнения окружающей среды Project_A
Project_A Типы связи слов в словосочетании
Типы связи слов в словосочетании Всероссийский флешмоб Голубь мира
Всероссийский флешмоб Голубь мира Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во
Работа головного мозга находится в прямой зависимости от качества нашего питания, чем оно лучше, тем выше наши интеллектуальные во БИОСИНТЕЗ
БИОСИНТЕЗ Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12
Сусымалы компоненттерді мөлшерлеу мен қоспалау желісі. Дарис 12