Содержание
- 2. Цели урока: Научиться раскладывать произвольный вектор по координатным векторам. Отработать навыки действий над векторами с заданными
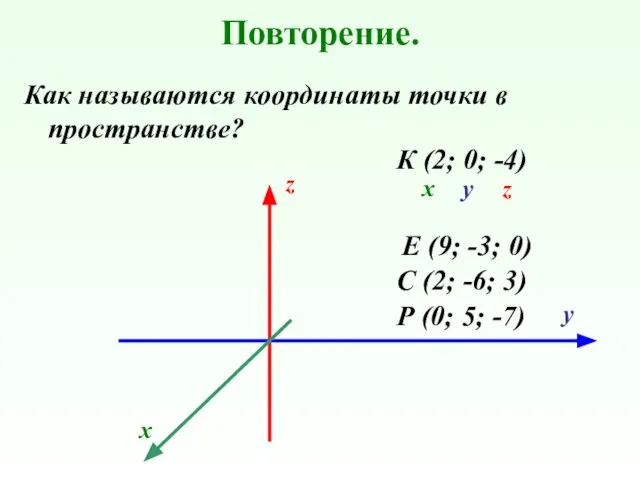
- 3. Повторение. Как называются координаты точки в пространстве? Р (0; 5; -7) К (2; 0; -4) С
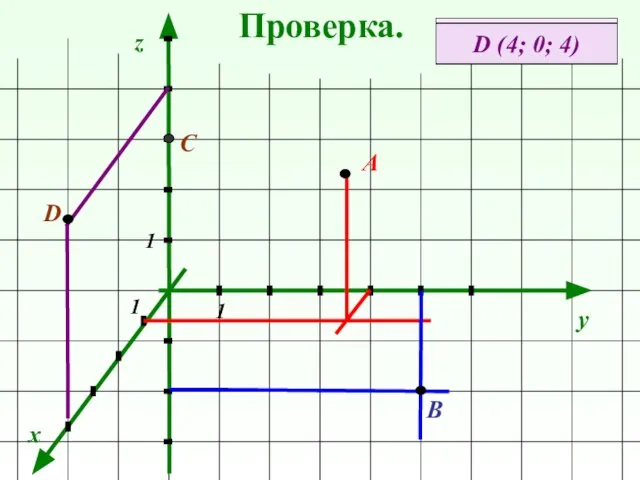
- 4. Повторение. Даны точки: А (2; -1; 0) В (0; 0; -7) С (2; 0; 0) D
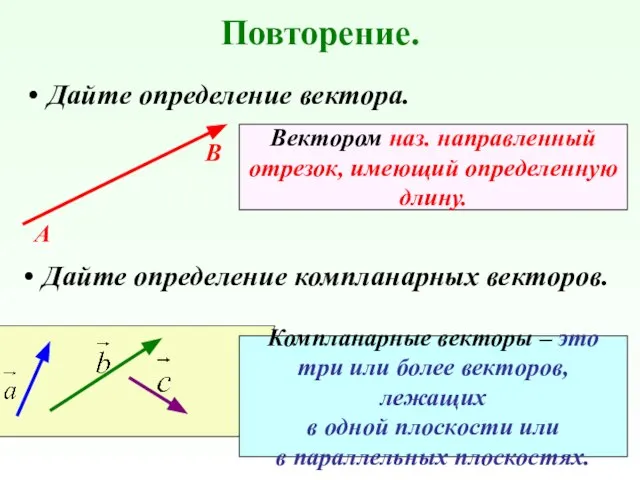
- 5. Повторение. Дайте определение вектора. А В Вектором наз. направленный отрезок, имеющий определенную длину. Дайте определение компланарных
- 6. Выполнение задания с последующей проверкой. Начертить прямоугольную трехмерную систему координат и отметить в ней точки: А
- 7. Проверка. x y z А (1; 4; 3) А В (0; 5; -3) 1 1 1
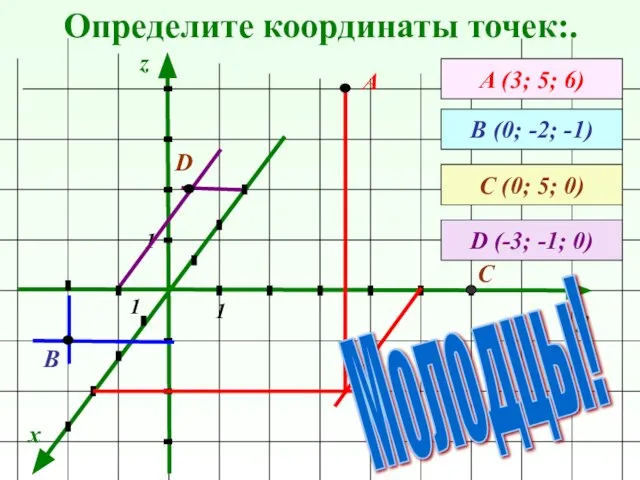
- 8. Определите координаты точек:. x y z А (3; 5; 6) А В (0; -2; -1) 1
- 9. Думаем… Отвечаем… Даны точки А (2; 4; 5), В (3; а; b), C (0; 4; d)
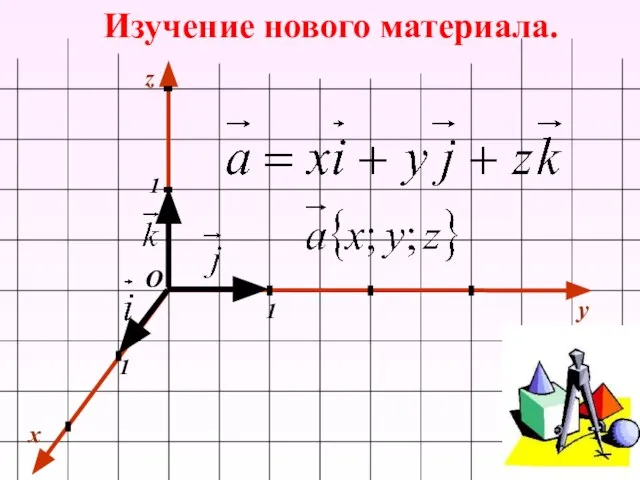
- 10. Изучение нового материала. x y 1 1 1 О z
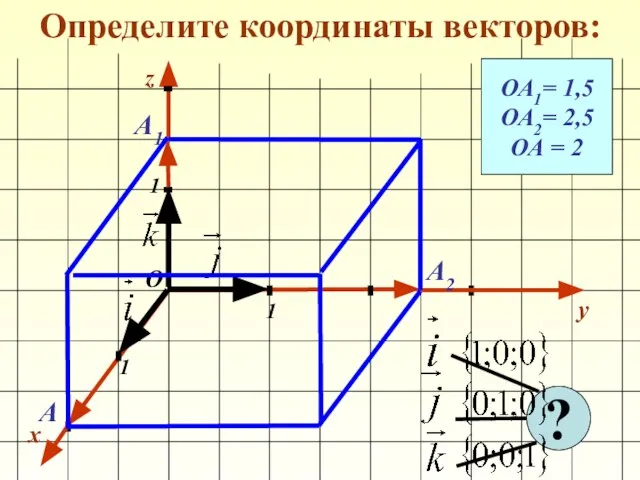
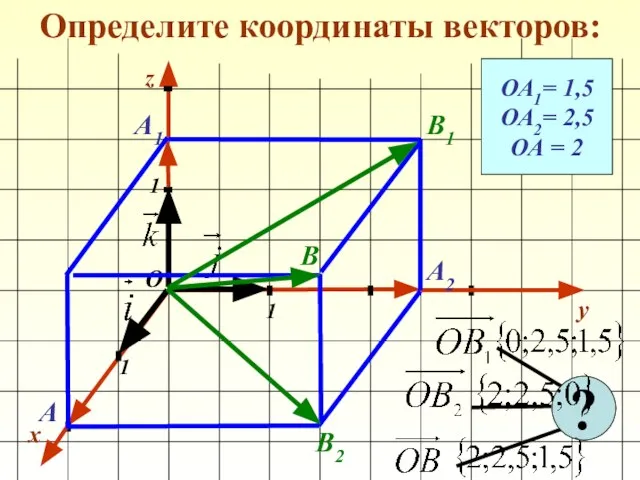
- 11. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 12. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
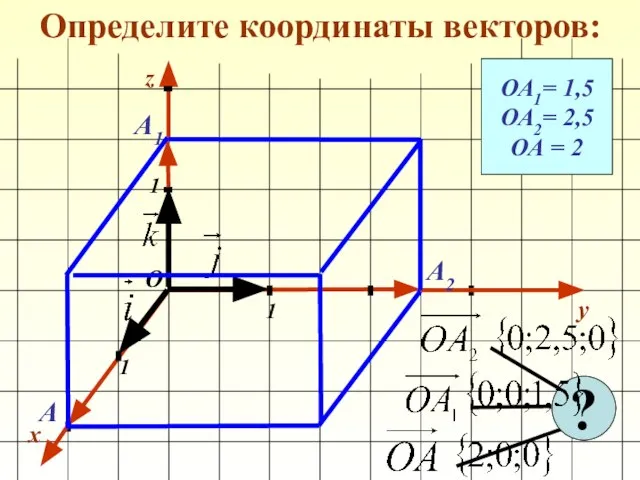
- 13. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 14. Разложите все векторы по координатным векторам. Проверяем:
- 15. Правила действий над векторами с заданными координатами. 1. Равные векторы имеют равные координаты. Пусть , тогда
- 16. Правила действий над векторами с заданными координатами. 2. Каждая координата суммы двух (и более) векторов равна
- 17. Правила действий над векторами с заданными координатами. 3. Каждая координата произведения вектора на число равна произведению
- 18. Домашнее задание: №№ 403, 404, 407 Доказательства двух правил действий над векторами. Повторить определение средней линии
- 19. Выполнить задание устно: Даны векторы: Найти вектор равный:
- 20. Письменно: №№ 403; 404; № 407 – по вариантам. I вариант – а, в, д. II
- 22. Скачать презентацию










 История одной девушки……..
История одной девушки…….. Объект и его свойства
Объект и его свойства Потребительская корзина
Потребительская корзина Виды общения в психологии
Виды общения в психологии От кареты до ракеты
От кареты до ракеты Отчёт депутата госдумы Шишкоедова В.М, партия Единая Россия
Отчёт депутата госдумы Шишкоедова В.М, партия Единая Россия Эндокринологическая аллея. Остановка Исторический музей
Эндокринологическая аллея. Остановка Исторический музей Стоимость системы Пион до конца 2020 года. Умный транспорт. ООО Софтлайн
Стоимость системы Пион до конца 2020 года. Умный транспорт. ООО Софтлайн Muqayise olunan dillerde sual cumleleri
Muqayise olunan dillerde sual cumleleri 1401470
1401470 Ремёсла на Кубани
Ремёсла на Кубани Source:
Source: Уклад и общественное управление
Уклад и общественное управление Презентация на тему НОРВЕГИЯ
Презентация на тему НОРВЕГИЯ  ПРАВИЛА ДОРОЖНОГО ДВИЖЕНИЯИ СТАТИСТИКА ДОРОЖНО-ТРАНСПОРТНЫХ ПРОИСШЕСТВИЙ
ПРАВИЛА ДОРОЖНОГО ДВИЖЕНИЯИ СТАТИСТИКА ДОРОЖНО-ТРАНСПОРТНЫХ ПРОИСШЕСТВИЙ K-POP
K-POP Устройство персонального компьютера
Устройство персонального компьютера Презентация на тему Состав чисел первого десятка
Презентация на тему Состав чисел первого десятка Оптимизация распределительной деятельности
Оптимизация распределительной деятельности Постимпрессионизм
Постимпрессионизм Opime koos! Учимся вместе!
Opime koos! Учимся вместе! Вы блестящий учитель, у Вас прекрасные ученики!
Вы блестящий учитель, у Вас прекрасные ученики! Презентация на тему Путь к свободе через красоту
Презентация на тему Путь к свободе через красоту Предмет, метод, система и источники трудового права
Предмет, метод, система и источники трудового права Магистерская программа
Магистерская программа ОТЕЧЕСТВЕННАЯ ВОЙНА 1812г.
ОТЕЧЕСТВЕННАЯ ВОЙНА 1812г. Лекция 1. Мировое хозяйство: понятие и сущность. МРТ.
Лекция 1. Мировое хозяйство: понятие и сущность. МРТ. Рынок мощности
Рынок мощности