Презентация на тему Обратные тригонометрические функции

Содержание:
Обратные тригонометрические функции, свойства, графики
Историческая справка
Преобразование выражений, содержащих обратные тригонометрические функции
Решение уравнений
Задания различного уровня сложности

Из истории тригонометрических функций
Древняя Греция.III в до н. э. Евклид, Аполоний Пергский. Отношения
сторон в прямоугольном треугольнике.
Ок. 190 до н. э Гиппарх Никейский. Возможно он первый составил
таблицу хорд, аналог современных таблиц тригонометрических функций.
Абу-аль-Ваф ввел тригонометрические функции тангенс и котангенс.
Первая половина XV в. Аль-Каши произвел уникальные расчеты, которые
были нужны для составления таблицы синусов с шагом 1’.
I-II вв. индийские математики вводят понятие синуса.
1423-1461- австрийский математик и астроном Георг фон Пойербах
был одним из первых европейских ученых, которрый применил
понятие синуса.
1602-1675 французский математик, астроном и физик Жиль Роберваль
построил синусоиду.
XV в. Региомонтан ввел термин тангенс.
1739 г. И. Бернулли ввел современные обозначения синуса и косинуса.
1770 г. Георг Симон Клюгель вводит новый термин тригонометрические
функции.
1772 г. Ж. Лагранж вводит первую из шести обратных тригонометрических
функций.
Карл Шерфер ввел современные обозначения для обратных
тригонометрических функций.

Arcsin х
Арксинусом числа m называется такой угол x, для которого sinx=m, -π/2≤X≤π/2,|m|≤1
Функция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей.
График обратной функции симметричен с графиком основной функции относительно биссектрисы I - III координатных углов.

Свойства функции y = arcsin x
1)Область определения: отрезок [-1; 1];
2)Область изменения: отрезок [-π/2,π/2];
3)Функция y = arcsin x нечетная: arcsin (-x) = - arcsin x;
4)Функция y = arcsin x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.

Arccos х
Арккосинусом числа m называется такой угол x, для которого:
cos x = m
0 ≤ x ≤ π
|m|≤1

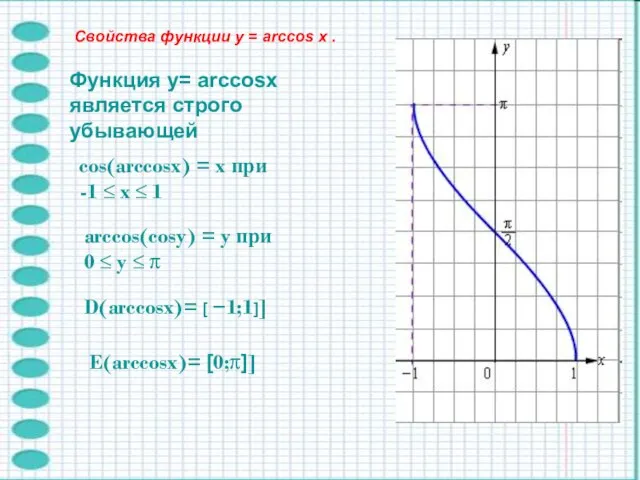
Функция y= arccosx является строго убывающей
cos(arccosx) = x при
-1 ≤ x ≤ 1
arccos(cosy) = y при
0 ≤ y ≤ π
D(arccosx)= [ −1;1]]
E(arccosx)= [0;π]]
Свойства функции y = arccos x .

Arctgх
Арктангенсом числа m
называется такой угол x,
для которого tgx=m,
-π/2
График функции y=arctgx
Получается из графика
Функции y=tgx, симметрией
Относительно прямой y=x.

y=arctgх
1)Область определения: R
2)Область значения: отрезок [-π/2,π/2];
3)Функция y = arctg x нечетная: arctg (-x) = - arctg x;
4)Функция y = arctg x монотонно возрастающая;
5)График пересекает оси Ох, Оу в начале координат.
y
y
x

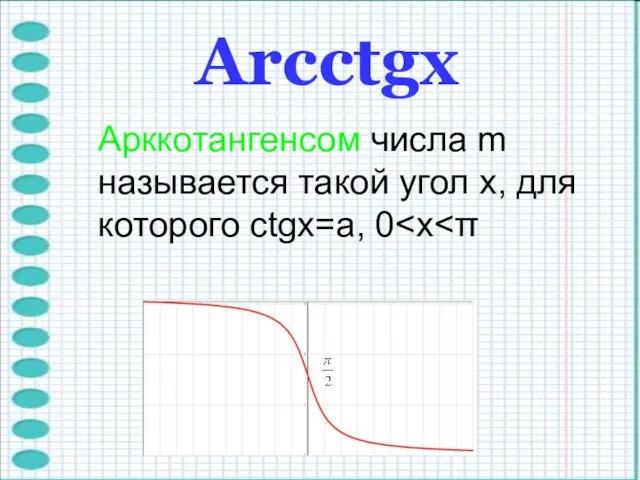
Arcctgх
Арккотангенсом числа m называется такой угол x, для которого ctgx=a, 0

Функция y=arcctgx непрерывна и ограничена на всей своей числовой прямой.
Функция y=arcctgx является строго убывающей.
ctg(arcctgx)=x при xєR
arcctg(ctgy)=y при 0 < y < π
D(arcctgx)=(-∞;∞)
E(arcctgx)=(0; π)
Arcctgх

Преобразование выражений

Преобразование выражений

Уравнения, содержащие
обратные тригонометрические функции

Упражнения для самостоятельного решения

Задания различного уровня сложности

Задания различного уровня сложности

Задания различного уровня сложности

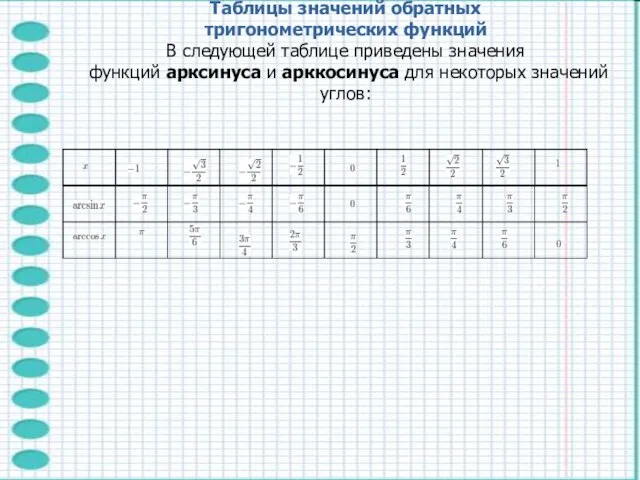
Таблицы значений обратных
тригонометрических функций
В следующей таблице приведены значения
функций арксинуса и арккосинуса для некоторых значений углов:

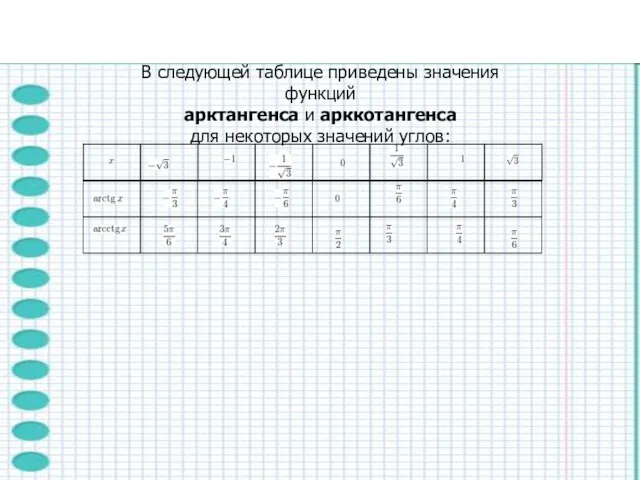
В следующей таблице приведены значения функций
арктангенса и арккотангенса
для некоторых значений углов: