Презентация на тему Отношения и пропорции

Вступление
"Впервые интерес к пропорции, возникающей при делении отрезка в крайнем и среднем отношении, возникает в античной науке (Пифагор, Платон, Евклид). Удивительные математические свойства этой пропорции уже тогда создают вокруг нее ореол таинственности и мистического поклонения".

Пропорция
Слово «пропорция» (от латинского propotio) означает «соразмерность», «определённое соотношение частей между собой».
В математике: равенство двух отношений

Возникновение учений об отношениях и пропорциях.
Учение об отношениях и пропорциях особенно успешно развивалось в IV веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.

Основное свойство пропорций
Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III век до нашей эры), там, в частности, приводится и доказательство основного свойства пропорции.
Оно звучит так: «В верной пропорции произведение крайних членов равно произведению средних.
a : b = c : d
средние
крайние
a · d = c · b

ПРОПОРЦИОНАЛЬНОСТЬ
Это простейший вид функциональной зависимости. Различают прямую пропорциональность. ( y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S = vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y = a/ x.

Свойства прямой пропорциональной зависимости
Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости)
Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.
Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.
Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх

Свойства обратной пропорциональной зависимости
Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.
Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.
Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным.
Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений у:
х1 / х2 = у2 / у1

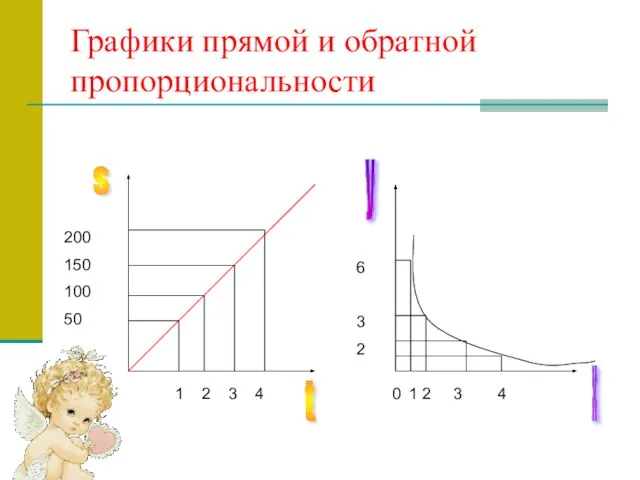
Графики прямой и обратной пропорциональности
1 2 3 4
200
150
100
50
s
t
у
х
0 1 2 3 4
6
3
2

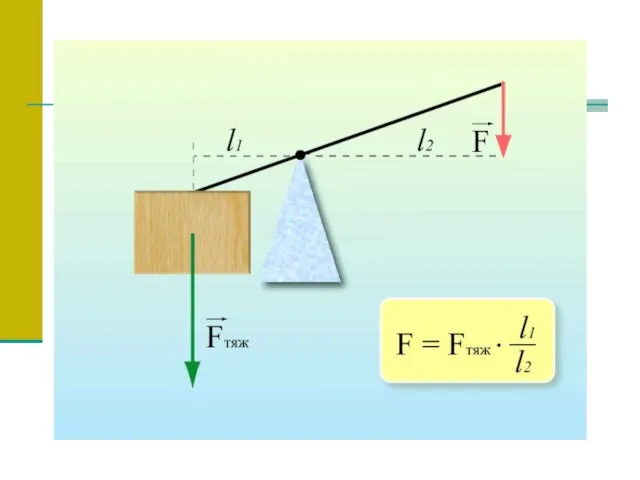
Пропорции в физике
С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией,
где M и m – массы грузов, а L и l – «плечи» рычага.

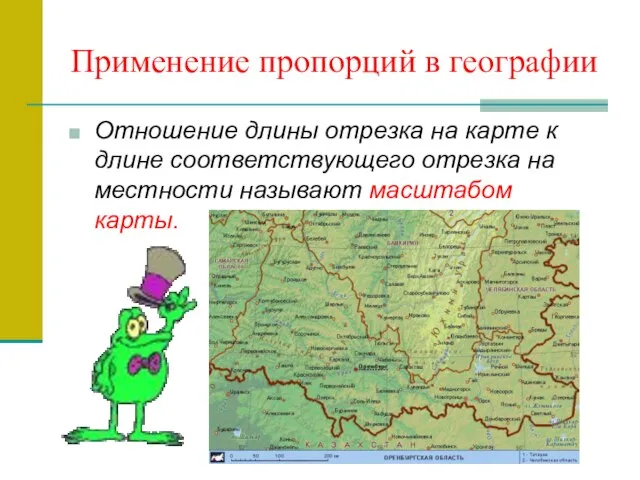
Применение пропорций в географии
Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.

Пропорциональность в других сферах жизни
Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.
Золотое сечение

ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.
Применение «золотого сечения» в архитектуре

АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)
«Золотое сечение» в искусстве

Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.

Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).

Задача
О применении математики в языкознании
В классе заболел учитель русского языка. Пришёл математик и стал объяснять падежи:
Именительный кто ? что ?
Родительный кого ? чего ?
Дательный кому ? а второй вопрос он забыл.
Тогда он сказал:
- Ничего, давайте обозначим его через x и составим пропорцию:
Итак, второй вопрос дательного падежа: чему ?

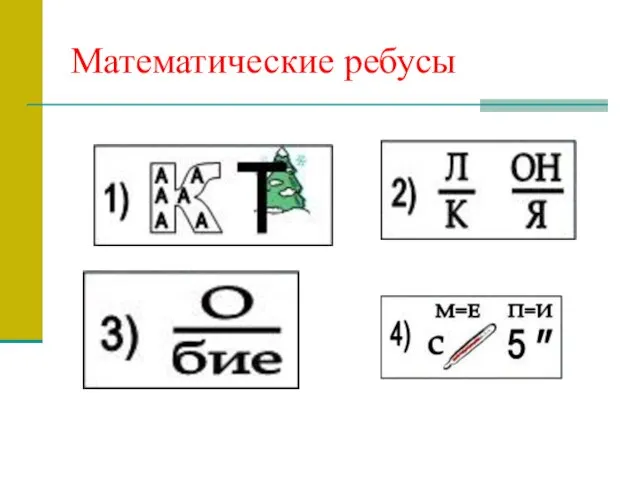
Математические ребусы

1.Показатель 2. Наклоная 3.Подобие 4.Стереометрия

Заключение
Пропорции сопровождают нас повсюду и являются неотъемлемой частью нашей жизни.
В своей презентации я привела только не большой перечень сфер где применяют пропорции. На самом деле этот список намного больше. Ведь пропорции появились одновременно с природой, даже до появления человека.