Содержание
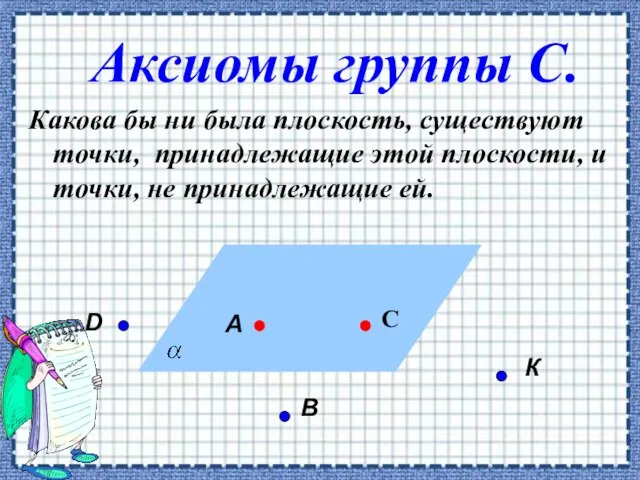
- 2. Аксиомы группы С. Какова бы ни была плоскость, существуют точки, принадлежащие этой плоскости, и точки, не
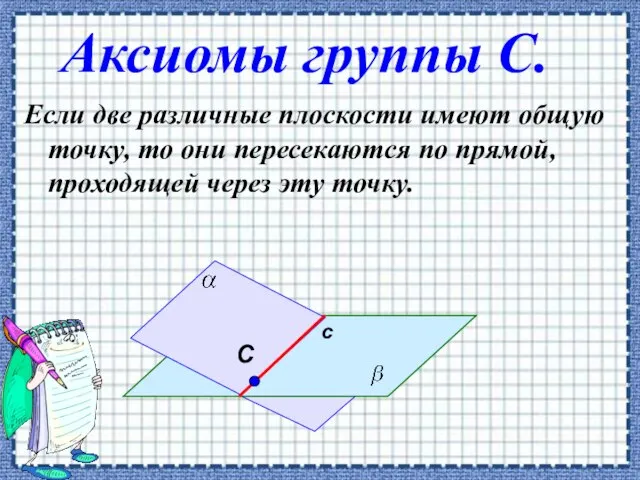
- 3. Аксиомы группы С. Если две различные плоскости имеют общую точку, то они пересекаются по прямой, проходящей
- 4. Аксиомы группы С. Если две различные прямые имеют общую точку, то через них можно провести плоскость,
- 5. Через любую прямую и не принадлежащую ей точку можно провести плоскость, и притом только одну.
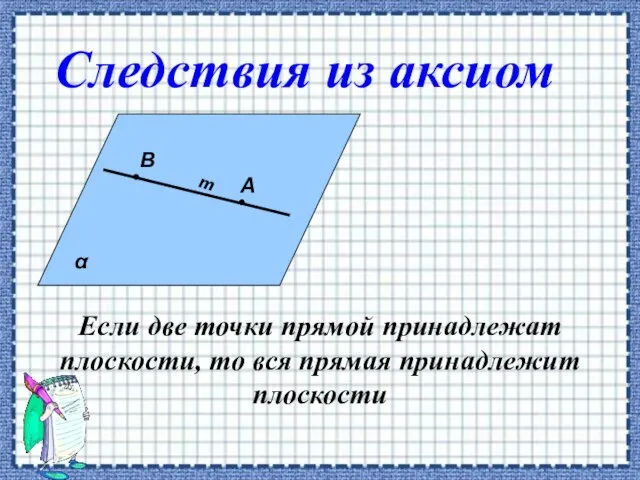
- 6. Если две точки прямой принадлежат плоскости, то вся прямая принадлежит плоскости А В Следствия из
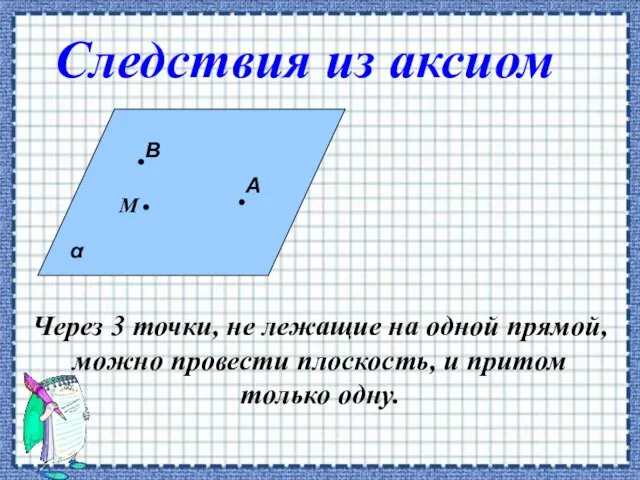
- 7. Через 3 точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.
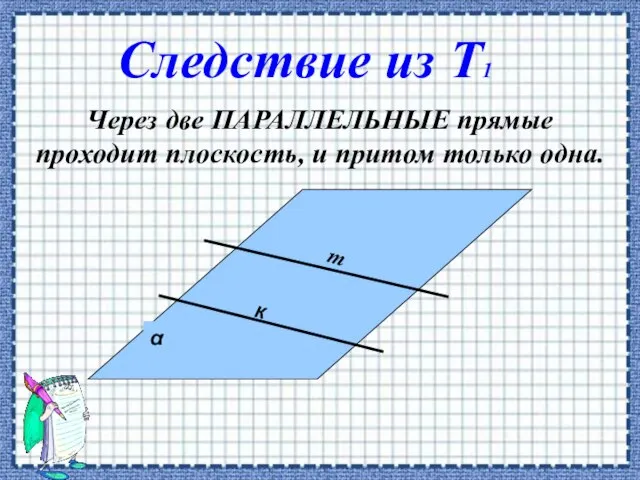
- 8. Через две ПАРАЛЛЕЛЬНЫЕ прямые проходит плоскость, и притом только одна. к Следствие из Т1
- 9. Вывод Как в пространстве можно однозначно задать плоскость? 1. По трем точкам 2. По прямой и
- 10. Сколько существует способов задания плоскости? Сколько плоскостей можно провести через выделенные элементы? а) б) в) г)
- 11. Нет Да Нет Да Нет Да Определите: верно, ли утверждение?
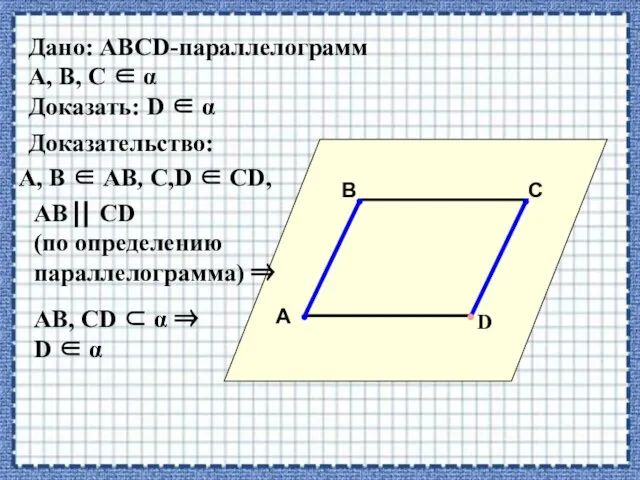
- 12. Дано: АВСD-параллелограмм А, В, С α Доказать: D α А В С D •
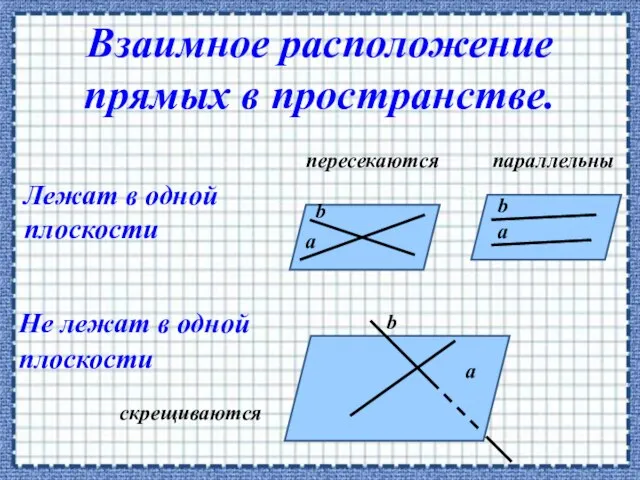
- 13. пересекаются параллельны а а а b b b скрещиваются Лежат в одной плоскости Не лежат в
- 14. Доказательство: а с в1 в β α В 1 случай. а, в, с α рассмотрен
- 15. Теорема о параллельных прямых. К a b Дано: К a Доказать: ! b: К
- 16. Задание 1 Вставьте пропущенные слова Единственную плоскость можно задать через три точки, при этом они на
- 17. Задание 2 Определите: верно, ли утверждение? Нет Нет Да Да Нет
- 18. Задание 2 Определите: верно, ли утверждение? Нет Нет Нет Да
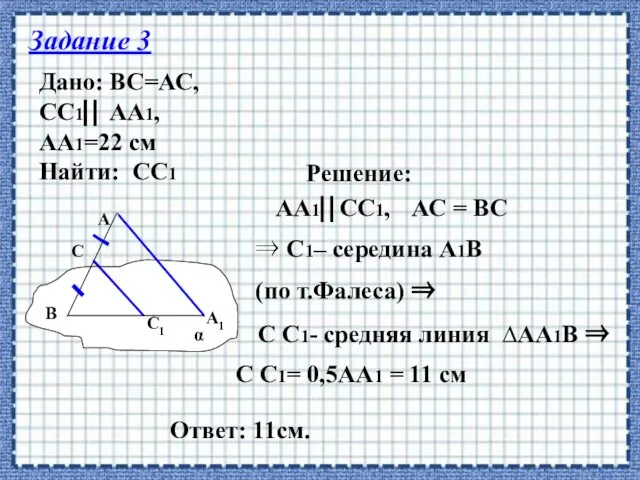
- 19. Задание 3 Дано: ВС=АС, СС1 АА1, АА1=22 см Найти: СС1 Решение: АА1СС1, АС = ВС
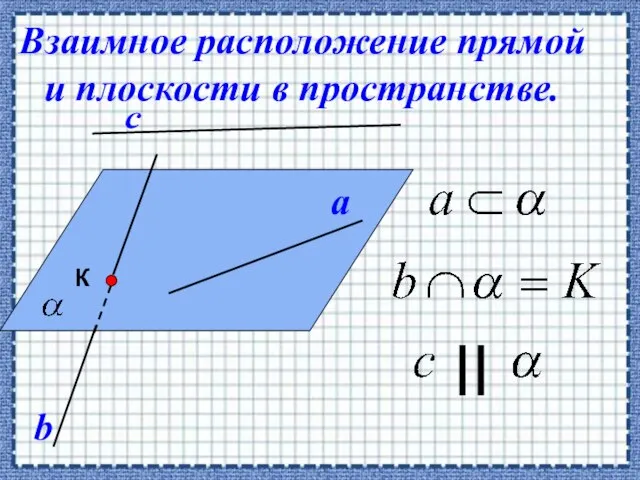
- 20. Взаимное расположение прямой и плоскости в пространстве.
- 21. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости , то
- 22. 1.Через прямые a и b проведем плоскость α Пусть , , α 2. α β
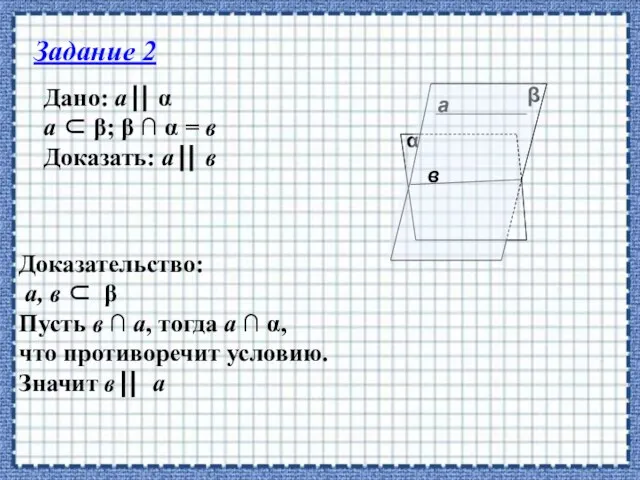
- 23. Дано: а α а β; β ∩ α = в Доказать: а в
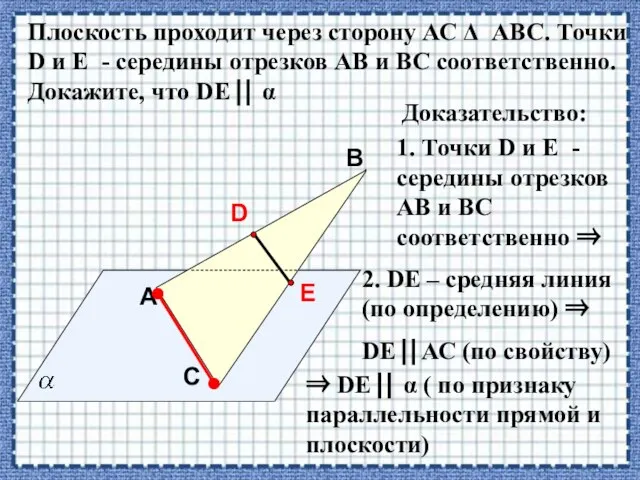
- 24. A В С Плоскость проходит через сторону АС АВС. Точки D и E - середины
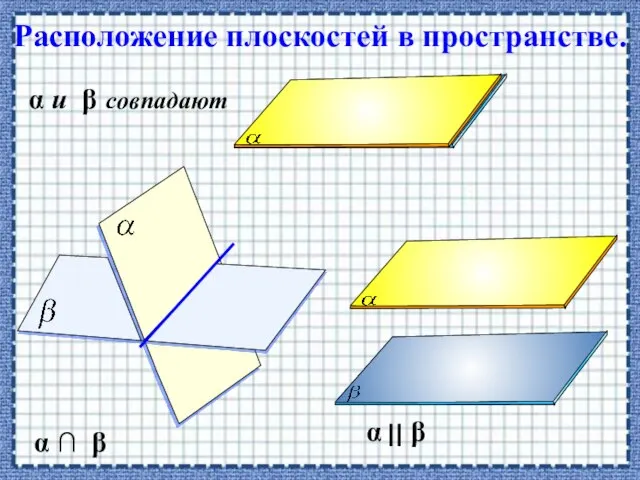
- 25. Расположение плоскостей в пространстве. α β α и β совпадают α β
- 26. Признак параллельности двух плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой
- 27. Теорема Через точку вне данной плоскости можно провести плоскость, параллельную данной, причём единственную. β а1 •
- 28. β • А α Докажем единственность плоскости β методом от противного. • С • В в
- 29. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. Свойство параллельных плоскостей. Дано: α
- 30. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. Свойство параллельных плоскостей. Доказать: АВ = СD Дано:
- 31. 1. если плоскости не пересекаются, то они параллельны. 2. плоскости параллельны, если прямая лежащая в одной
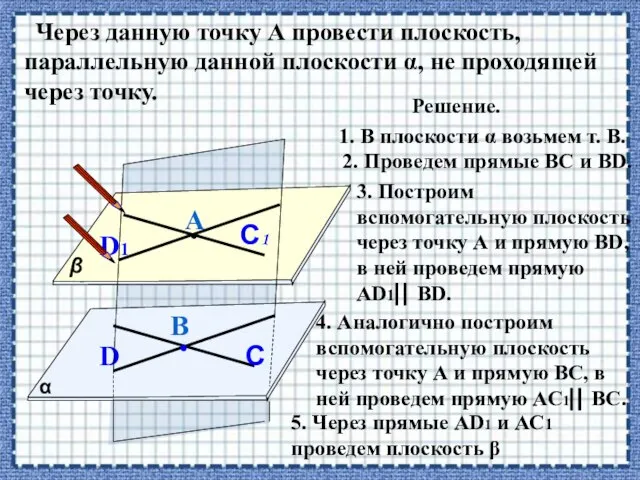
- 32. Через данную точку А провести плоскость, параллельную данной плоскости α, не проходящей через точку. α β
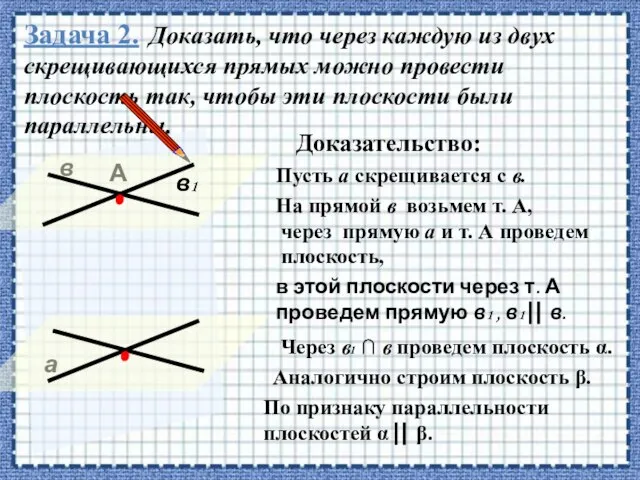
- 33. Задача 2. Доказать, что через каждую из двух скрещивающихся прямых можно провести плоскость так, чтобы эти
- 35. Скачать презентацию


















 45%
45% Молодёжные субкультуры
Молодёжные субкультуры Сила упругости. Закон Гука
Сила упругости. Закон Гука 03.2016 Гуляев Р.А. Дубровина Т.Л
03.2016 Гуляев Р.А. Дубровина Т.Л Язык живописи. Перспектива
Язык живописи. Перспектива Презентация на тему Агропромышленный комплекс Легкая и пищевая промышленность
Презентация на тему Агропромышленный комплекс Легкая и пищевая промышленность К 240- летию со дня рождения
К 240- летию со дня рождения Программа автоматизации организации школьного питания «Вижен-Софт:Питание в школе»
Программа автоматизации организации школьного питания «Вижен-Софт:Питание в школе» Презентация на тему If I went to Britain
Презентация на тему If I went to Britain Прокуратура РФ
Прокуратура РФ Научно-исследовательский институт столичного образования в научном комплексе МГПУ
Научно-исследовательский институт столичного образования в научном комплексе МГПУ Удивительный мир веществ
Удивительный мир веществ Опыт и уроки формирования методологии реализации проекта NCSA
Опыт и уроки формирования методологии реализации проекта NCSA растительный мир
растительный мир Огневая подготовка
Огневая подготовка История изменения моды в Англии XX-XXI веков
История изменения моды в Англии XX-XXI веков Салаты
Салаты Зонирование (00000002)
Зонирование (00000002) Системы смягчения рисков в сельской местности
Системы смягчения рисков в сельской местности Костюм Западной Европы XIX века
Костюм Западной Европы XIX века Рекомендательный аннотированный список русской детской и современной детской литературы. Составлен библиотекарем гимнази
Рекомендательный аннотированный список русской детской и современной детской литературы. Составлен библиотекарем гимнази Художественное объединение Голубая роза
Художественное объединение Голубая роза ОСНОВНЫЕ НАПРАВЛЕНИЯ ДЕЯТЕЛЬНОСТИ
ОСНОВНЫЕ НАПРАВЛЕНИЯ ДЕЯТЕЛЬНОСТИ Какой я
Какой я Урок-игра "Обыкновенные дроби"
Урок-игра "Обыкновенные дроби" Правила описания объекта закупки (ПООЗ) 44 -ФЗ
Правила описания объекта закупки (ПООЗ) 44 -ФЗ Рынок инновационной продукции: понятие, субъект, объект, отличительные особенности
Рынок инновационной продукции: понятие, субъект, объект, отличительные особенности Разработка мероприятий по совершенствованию систем контроля качества демонтажных работ
Разработка мероприятий по совершенствованию систем контроля качества демонтажных работ