Содержание
- 2. Определение: Функция F(х) называется первообразной функции f(х) на промежутке Х, если Теорема: Если функция f(х) непрерывна
- 3. Пример: Решение. Данная функция может быть записана в виде:
- 4. Замечание 2: Если функция f(х) определена на промежутке Х и в точке имеет разрыв в виде
- 5. Основные свойства неопределенного интеграла.
- 6. Основные методы Интегрирования.
- 7. Табличный. Сведение к табличному преобразованием подынтегрального выражения в сумму или разность. Интегрирование с помощью замены переменной
- 8. Нахождение интеграла методом преобразования подынтегральной функции в сумму или разность.
- 9. Интегрирование методом замены переменной.
- 11. Интегрирование выражений, содержащих радикалы, методом подстановки.
- 13. Интегрирование алгебраических дробей.
- 14. Интегрирование по частям.
- 17. Скачать презентацию














 Антон Павлович Чехов Толстый и тонкий
Антон Павлович Чехов Толстый и тонкий ДЕПАРТАМЕНТ ПО СОЦИАЛЬНЫМ ВОПРОСАМ Муниципальное образовательное учреждение для детей-сирот и детей, оставшихся без попечения р
ДЕПАРТАМЕНТ ПО СОЦИАЛЬНЫМ ВОПРОСАМ Муниципальное образовательное учреждение для детей-сирот и детей, оставшихся без попечения р Neuropsychology of Memory
Neuropsychology of Memory  Синтетические волокна: полиуретановые и полиакрилонитрильные волокна
Синтетические волокна: полиуретановые и полиакрилонитрильные волокна Организация как объект менеджмента
Организация как объект менеджмента Геология
Геология  Эмоции и традиционное общество
Эмоции и традиционное общество Андрей Матвеев
Андрей Матвеев Инновационные перспективы преподавания валеологического компонента в структуре базовых клинических дисциплин Реализация мер
Инновационные перспективы преподавания валеологического компонента в структуре базовых клинических дисциплин Реализация мер Виды повреждений ТС
Виды повреждений ТС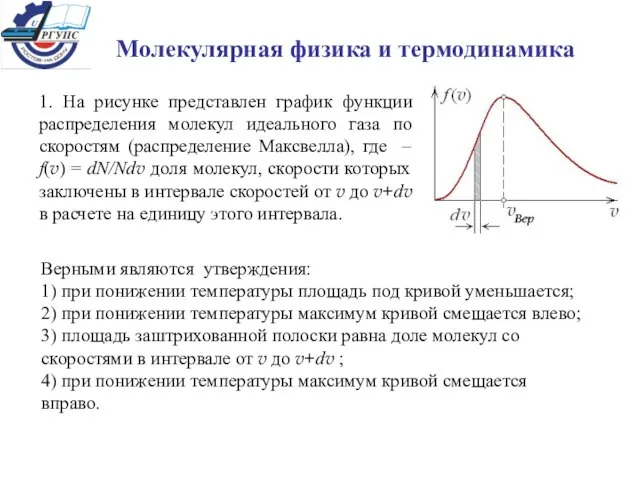 Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Жизнь 8а
Жизнь 8а ХАРАКТЕРИСТИКА ТУНДР
ХАРАКТЕРИСТИКА ТУНДР 2012 – год российской истории
2012 – год российской истории Наш кандидат - Миншаехова Дарья
Наш кандидат - Миншаехова Дарья Начало подросткового возраста
Начало подросткового возраста Презентация на тему Применение компьютерных технологий в обучении младших классов
Презентация на тему Применение компьютерных технологий в обучении младших классов  Жесты судей
Жесты судей Текстовый редактор Microsoft Word Одной из наиболее широких сфер использования компьютеров является обработка текстовой информации: ре
Текстовый редактор Microsoft Word Одной из наиболее широких сфер использования компьютеров является обработка текстовой информации: ре Куликовская битва 4 класс - тест
Куликовская битва 4 класс - тест 48843
48843 Презентация Института оценки программ и политик (ИОПП) 2008 г.
Презентация Института оценки программ и политик (ИОПП) 2008 г. Поговорим о любимых домашних питомцах
Поговорим о любимых домашних питомцах Павел Мишарин - свадебный фотограф
Павел Мишарин - свадебный фотограф Торговые организации Башкортостана
Торговые организации Башкортостана Проект "Выпекаем праздник"
Проект "Выпекаем праздник" Правда о диете
Правда о диете Религия как форма культуры
Религия как форма культуры