Презентация на тему Рациональные уравнения

В данной презентации достаточно полно
изложена теория решения различных видов
рациональных уравнений,
за исключением линейных и квадратных
уравнений, а также общей теории
решения уравнений 3-й и 4-й степеней.
Нет здесь и примеров, решаемых
с помощью теоремы Безу.
Каждый вид уравнения сопровождается
решением соответствующего примера.
Данные материалы могут быть использованы
частично на уроках алгебры
в обычных классах,
но в большей мере пригодятся
для изучения этой темы
в классах с углубленным изучением
математики.

end

end

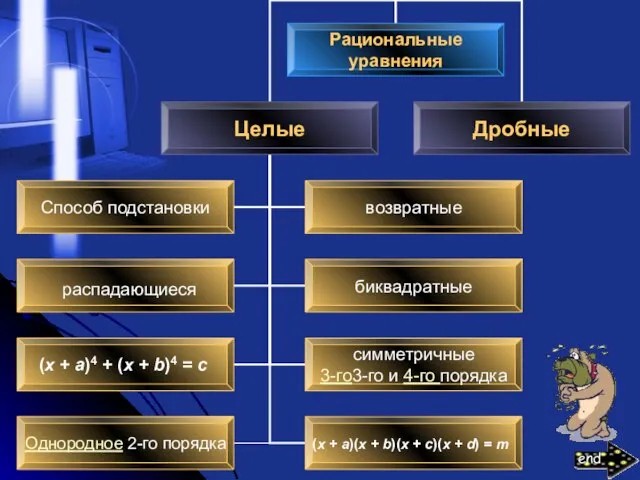
Способ подстановки
При решении некоторых целых рациональных уравнений есть смысл ввести новую переменную величину, обозначив некоторое рациональное выражение новой буквой.
Например, в уравнении ,
где Р(х) – многочлен, удобно ввести новую
переменную y=Р(х), решить полученное
квадратное уравнение
относительно y и, наконец, решить
уравнение Р(х)= yо, где yо – корень
уравнения
Обратно
в меню
Пример

Пример
Решите уравнение
Решение. Введем новую переменную. Пусть
Тогда получим уравнение
Находим корень у = 1 и делаем обратную подстановку.
Ответ: 2; 3.
Обратно
в меню

Распадающееся уравнение
Рациональное уравнение называется распадающимся, если его можно привести к виду , где – рациональные выражения с переменной х.
Для решения воспользуемся равносильным переходом
Применяемые приемы разложения на множители:
- вынесение общего множителя за скобки;
- способ группировки;
-формулы сокращенного умножения.
Обратно
в меню
Пример

Пример
Решите уравнение
Решение. Разложим левую часть уравнения на множители:
Воспользуемся равносильным переходом:
Ответ:-2;0;1;2.
Обратно
в меню

Однородное уравнение 2-го порядка
При решении уравнения надо проверить две ситуации:
1) т.е. корнями заданного уравнения
являются решения этой системы.
2) Если Q(x) ≠ 0, то после деления заданного уравнения на Q2(x) получим уравнение
которое подстановкой сводится
к квадратному уравнению
В ответ включают числа, полученные
при рассмотрении обеих ситуаций.
Обратно
в меню
Пример

Пример
Решить уравнение
(x2 – 2х)2 – (x2 – 2х)(x2 – х – 2) – 2(x2 – х – 2)2 = 0.
Решение. Возможны две ситуации.
Рассмотрим первую:
Обратно
в меню
Найден первый корень уравнения х=2.

Продолжение решения
Рассмотрим вторую ситуацию: разделим почленно заданное уравнение на (x2 – х – 2)2 при условии, что х ≠ -1 и х ≠ 2. Уравнение принимает вид
Обозначим и решим квадратное
уравнение t2 – t –2 = 0. Получаем t1= -1, t2= 2.
Обратная подстановка дает уравнения
откуда х = -0,5 и х = -2.
С учетом обеих ситуаций получаем
ответ: - 0,5; -2; 2.
Обратно
в меню

Биквадратное уравнение
Уравнение имеет вид
aх4+bх2+c=0.
Сделаем подстановку x2 = t. Значит, x4 = t2.
Получаем квадратное уравнение
at2+bt+c=0.
Находим значения t и, сделав обратную подстановку, находим корни исходного уравнения.
Замечание.
При решении биквадратного уравнения можно
получить от 1 до 4-х корней или же это
уравнение может совсем не иметь корней.
Обратно
в меню
Пример

Пример
Решите уравнение х4–3х2–4=0.
Решение.
Сделаем подстановку x2 = t. Получаем квадратное уравнение
t2–3t–4=0,
корни которого t = -1 и t = 4.
Обратная замена дает два уравнения
x2 = -1 и x2 = 4, из которых первое уравнение не имеет корней, а корни второго уравнения -2 и 2.
Ответ: -2; 2.
Обратно
в меню

Симметричное уравнение
3-го порядка
Уравнение имеет вид
ах3+bх2+bх+а=0.
Сгруппируем слагаемые: а(х3+1)+bх(х+1)=0.
Применим формулу суммы кубов
а(х+1)(х2 –х+1)+bх(х+1)=0
и выполним разложение на множители
(х+1)(ах2+(b - а)х+а)=0.
Получили распадающееся уравнение. Значит,
х+1=0 или ах2+(b - а)х+а=0.
Решив эти два уравнения, найдем корни
исходного уравнения.
Обратно
в меню
Пример

Пример
Решите уравнение 2х3–3х2– 3х +2=0.
Решение. Сгруппируем слагаемые парами и в каждой паре вынесем общий множитель за скобки:
2(х3+1)–3х(х+1)=0.
Применим формулу суммы кубов и вынесем общий множитель (х+1):
2(х+1)(х2 –х+1)– 3х(х+1)=0,
(х+1)(2х2 –5х+2)=0.
Значит,
х+1=0 или 2х2 –5х+2=0.
Решив эти два уравнения, найдем корни
исходного уравнения: -1; 0,5; 2.
Ответ: -1; 0,5; 2.
Обратно
в меню

Симметричное уравнение
4-го порядка
Уравнение имеет вид
ах4+bх3+сх2+bх+а=0.
Сгруппируем слагаемые и разделим обе части уравнения на х2. Получаем
Сделаем подстановку , тогда
Получаем квадратное уравнение
a(t2-2)+bt+c=0.
Находим значения t и делаем обратную подстановку.
Обратно
в меню
Пример

Пример
Решите уравнение
Решение. Разделим обе части уравнения на x2 ≠ 0 и, удобно группируя, получим равносильное уравнение:
Сделаем подстановку , тогда
Получаем квадратное уравнение , корни
которого 2 и -3,5.
Обратная подстановка дает два рациональных
уравнения и
откуда и находим корни исходного уравнения.
Ответ: 1;
Обратно
в меню

Возвратное уравнение
Уравнение вида
ax4 + bx3 + cx2 + dx + e = 0,
где a ≠ 0, b ≠ 0 и ,
называется возвратным уравнением четвертого порядка.
Это уравнение сводится к квадратному с
помощью подстановки
Обратно
в меню
Пример

Пример
Решить уравнение
x4 + x3 - 6x2 - 2x + 4 = 0.
Решение. Заметим, что и, следовательно, данное уравнение есть возвратное уравнение четвертого порядка.
Так как x = 0 не является решением уравнения, разделим на x2 и получим равносильное уравнение
Обозначим , тогда
и уравнение примет вид t2 + t - 2 = 0, корни которого t1 = -2 и t2 = 1.
Делаем обратную замену и после умножения на x ≠ 0
получаем два квадратных уравнения
x2 + 2x - 2 = 0, x2 - x - 2 = 0,
откуда и получим корни исходного уравнения.
Ответ:
Обратно
в меню

Уравнения вида
(x + a)(x + b)(x + c)(x + d) = m
Если a + b = c + d , то это уравнение сводится к квадратному уравнению. Действительно,
(x + a)(x + b) = x2 + (a + b)x + ab
(x + c)(x + d) = x2 + (c + d)x + cd =
= x2 + (a + b)x + cd
Обозначив x2 + (a + b)x = t, получим квадратное
уравнение
(t + ab)(t + cd) = m
Из этого уравнения найдем значения t и,
сделав обратную подстановку, закончим
решение исходного уравнения.
Обратно
в меню
Пример

Пример
Решить уравнение
(x - 2)(x + 1)(x + 4)(x + 7) = 19.
Решение. Заметим, что -2 + 7 = 1 + 4. Удобно группируя, получим
[(x - 2)(x + 7)]·[(x + 1)(x + 4)] = 19
или
(x2 + 5x – 14 )(x2 + 5x + 4) = 19.
Обозначим t = x2 + 5x - 14, тогда x2 + 5x + 4 = t + 18.
Уравнение примет вид
t(t + 18) = 19 или t2 + 18t - 19 = 0,
откуда t = -19 и t = 1.
Сделав обратную подстановку, получим
x2 + 5x - 14 = -19 и x2 + 5x - 14 = 1.
Окончательный ответ:
Обратно
в меню

Уравнение вида
(x + a)4 + (x + b)4 = c
Используя подстановку , уравнение
можно свести к биквадратному уравнению относительно t.
Действительно, подставив в уравнение , получим
Обозначим и возведем
каждое слагаемое в 4-ю степень. После приведения
подобных получим биквадратное уравнение
Обратно
в меню
Пример

Пример
Решить уравнение
(x + 3)4 + (x - 1)4 = 82.
Решение. Сделаем подстановку
Получим следующее уравнение относительно t:
(t + 2)4 + (t - 2)4 = 82
или
t4 + 8t3 + 24t2 + 32t + 16 + t4 - 8t3 + 24t2 - 32t + 16 - 82 = 0.
Откуда получим биквадратное уравнение
t4 + 24t2 - 25 = 0,
корни которого t = ± 1.
Следовательно, x + 1 = ± 1.
Значит, корни исходного уравнения
x = -2 и x = 0.
Ответ: -2;0.
Обратно
в меню

Уравнение вида
Решить уравнение Р(х) = 0.
Для каждого корня уравнения Р(х) = 0
сделать проверку: удовлетворяет ли он
условию Q(х) ≠ 0 или нет. Если да, то
это — корень заданного уравнения,
а если нет, то этот корень является
посторонний для заданного уравнения
и в ответ его включать не следует.
Обратно
в меню
Пример

Пример
Решите уравнение
Решение.
Приравняем числитель дроби к нулю и решим полученное уравнение:
Значение х = 2 не удовлетворяет условию
Следовательно, уравнение имеет один
корень х= 4.
Ответ: 4.
Обратно
в меню

Уравнение вида
Подстановкой это уравнение
сводится к виду
Умножим на и решим полученное квадратное
уравнение относительно t.
Остается сделать обратную подстановку
где tо - корень квадратного уравнения,
и решить полученное уравнение
относительно х.
Обратно
в меню
Пример

Уравнение вида
Подстановкой это уравнение
сводится к виду
Умножим на и решим полученное квадратное
уравнение относительно t.
Остается сделать обратную подстановку
где tо - корень квадратного уравнения,
и решить полученное уравнение
относительно х.
Обратно
в меню
Пример

Пример
Решите уравнение
Решение.
Сделаем подстановку и решим полученное уравнение относительно t :
Обратная подстановка приводит к уравнению
корень которого х = -1.
Ответ: -1.
Обратно
в меню

Уравнения, состоящие из суммы двух и более дробей
1-й способ
Перенести все члены уравнения
в одну часть.
Привести уравнение к виду и найти корни полученного уравнения.
2-й способ
Определить О.Д.З. уравнения.
Умножить обе части уравнения на общий знаменатель дробей и получить целое уравнение.
Найти корни полученного уравнения и проверить их соответствие О.Д.З.
Обратно
в меню
Пример

Пример
Решите уравнение
Решение. Найдём О.Д.З. Знаменатели дробей не могут обращаться в нуль . Значит, О.Д.З. уравнения: х ≠ 2 и х ≠ 0.
Перенесём члены из правой части уравнения в левую и приведём к общему знаменателю.
.
Приравняем числитель дроби к нулю: х2 – 6х + 8 = 0.
Находим корни квадратного уравнения: х = 4 и х = 2.
Значение х = 2 не удовлетворяет О.Д.З.
Следовательно, уравнение имеет один корень х= 4.
Ответ: 4.
Обратно
в меню

Уравнения вида
Данное уравнение сводится к квадратному уравнению заменой переменной
Обратно
в меню
Пример

Пример
Решить уравнение
Решение. О.Д.З. уравнения есть множество
Поскольку x = 0 не является решением данного уравнения, перепишем уравнение в виде
(разделим числитель и знаменатель каждой дроби на x).
Обозначим и уравнение примет вид
Обратно
в меню

Продолжение решения
О.Д.З. полученного уравнения t ≠ 5 и t ≠ -1. Решая это уравнение, приходим к квадратному уравнению
2t2 - 13t + 11 = 0,
корни которого t1 = 1 и t2 = 11/2 удовлетворяют О.Д.З..
Делаем обратную подстановку и получаем два
рациональных уравнения
решив которые находим корни заданного
уравнения.
Ответ:
Обратно
в меню