Содержание
- 2. Скорость и ускорение при движении точки в пространстве Для характеристики движения материальной точки в пространстве вводится
- 3. Направление вектора средней скорости совпадает с направлением . При неограниченном уменьшении t средняя скорость стремится к
- 4. Аналогично определяются величины среднего и мгновенного ускорения:
- 5. В общем случае полное ускорение можно представить в виде векторной суммы тангенциального и нормального ускорений Тангенциальная
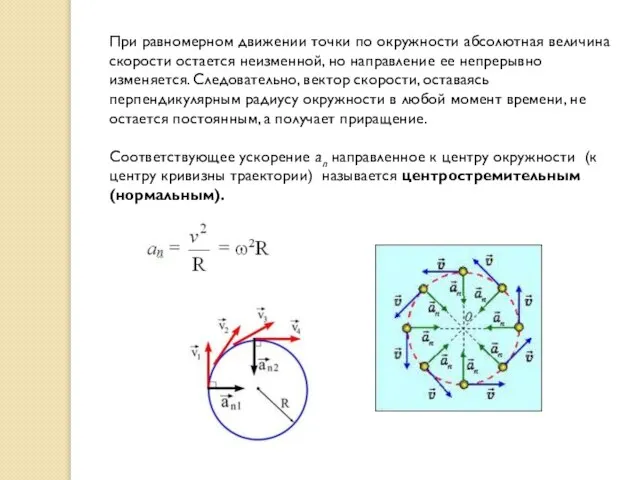
- 6. Нормальная составляющая ускорения равна где v – скорость, R – радиус кривизны траектории в данный момент
- 7. Известно, что в году приблизительно пи на десять в седьмой секунд. И это просто объяснить с
- 8. Кинематика вращательного движения Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела
- 9. Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени: Вектор направлен вдоль
- 10. Отдельные точки вращающегося тела имеют различные линейные скорости . Скорость каждой из точек непрерывно изменяет свое
- 11. Вектор может изменяться как за счет изменения скорости вращения тела вокруг оси (в этом случае он
- 12. При равномерном движении точки по окружности абсолютная величина скорости остается неизменной, но направление ее непрерывно изменяется.
- 13. Задание. Тело, имея начальную скорость 4 м/с, прошло за шестую секунду движения путь 2,9 м. Найти
- 14. Задание. Автомобиль, находясь на расстоянии 50 м от светофора и имея в этот момент скорость 36
- 15. Задание. Определить центростремительное ускорение точек земной поверхности на экваторе, на широте и на полюсе, вызванное вращением
- 16. 2.Линейная скорость точки В земной поверхности, находящейся на широте φ, равна где r - радиус окружности,
- 17. Задание. Во сколько раз нужно увеличить скорость брошенного вверх тела, чтобы высота подъема увеличилась в 4
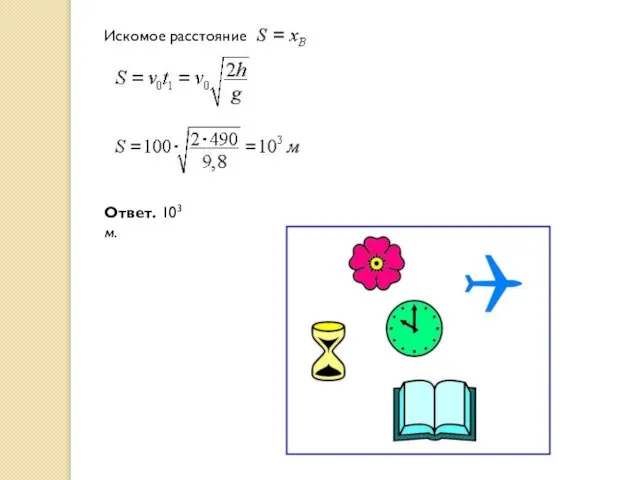
- 18. Задание. Самолет летит горизонтально со скоростью 360 км/ч на высоте 490 м. Когда он пролетает над
- 19. Искомое расстояние Ответ. 103 м.
- 20. Вопросы на внимание по предыдущему рисунку. 1. Есть ли в книге картинки? 2. В какую сторону
- 21. Динамика материальной точки и поступательного движения твердого тела Кинематика описывает движение тел, не затрагивая его причин.
- 22. Первый закон Ньютона. Масса и импульс тела. Сила Динамика является основным разделом механики, в ее основе
- 23. Система отсчета, в которой выполняется первый закон Ньютона, называют инерциальной системой отсчета. Инерциальной системой отсчета является
- 24. История выбора "правильной" системы отсчета Этот выбор в первую очередь связан с системой мира Коперника. Интересно
- 25. Клавдий Птолемей (ок. 90–ок. 160 нашей эры). Птолемей родился в Александрии (Египет), древний астроном, географ и
- 26. Николай Коперник - прославленный астроном из Польши(1473-1543). Николай Коперник отодвинул в сторону общепринятые представления о геоцентрической
- 27. Гелиоцентрическая система в варианте Коперника может быть сформулирована в семи утверждениях: Орбиты и небесные сферы не
- 28. Джордано Бруно (1548-1600) пострадал от рук инквизиции: 17 февраля 1600 года мыслитель был сожжен на Площади
- 29. Иоган Кеплер (1571-1630) – Выдающийся немецкий астроном и математик, открывший законы движения планет вокруг Солнца. Кеплер
- 30. Первый закон Кеплера предполагает, что Солнце находится не в центре эллипса, а в особой точке, называемой
- 31. Галилео Галилей (1564-1642), итальянский физик, механик и астроном, один из основателей естествознания Нового времени. …семидесятилетний больной
- 32. Вся жизнь великого ученого свидетельствует, что, уступая злой, слепой силе, он не смирился. Он открыл горы
- 33. Это Галилей первым вывел формулу: пройденный падающим телом путь пропорционален квадрату времени падения. Он первым определил,
- 34. Эксперимент Фуко Впервые публичная демонстрация была осуществлена Фуко в 1851 г. в Парижском Пантеоне: под куполом
- 35. В Исаакиевском соборе маятник Фуко был запущен в ночь с 11 на 12 апреля 1931 года.
- 36. Физика эксперимента Фуко Маятник Фуко является математическим маятником, такой маятник, отклонённый от равновесного положения, совершает колебания
- 38. Скачать презентацию

































 Политика и власть
Политика и власть А.С.Пушкин «Барышня-крестьянка»
А.С.Пушкин «Барышня-крестьянка» Билингвальный профориентационный проект. АтомГлосс. Тверская гимназия №8
Билингвальный профориентационный проект. АтомГлосс. Тверская гимназия №8 Содержание и методика подготовки исследовательских работ обучающихся по краеведению
Содержание и методика подготовки исследовательских работ обучающихся по краеведению Конфликты
Конфликты 2009 год.
2009 год. Каталог столярных изделий
Каталог столярных изделий JPA International Аудит - Гарант. Аудиторлық желі
JPA International Аудит - Гарант. Аудиторлық желі 1
1 Здравствуй, праздник Новый год!
Здравствуй, праздник Новый год! Восхождение на Килиманджаро
Восхождение на Килиманджаро Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Построение проекций точек на поверхностях тел и предметов. Урок черчения
Построение проекций точек на поверхностях тел и предметов. Урок черчения «Очистка воздушных масс»
«Очистка воздушных масс» Разработка мероприятий по безопасности технологического процесса производтсва в ООО Северные тепловые сети
Разработка мероприятий по безопасности технологического процесса производтсва в ООО Северные тепловые сети Река Медведица
Река Медведица Презентация по биологии по теме «Система кровообращения»
Презентация по биологии по теме «Система кровообращения» Мир фотографии
Мир фотографии Активные формы и методы работы по развитию творческих способностей на уроках и во внеурочной деятельности
Активные формы и методы работы по развитию творческих способностей на уроках и во внеурочной деятельности Диаграммы и графики
Диаграммы и графики Управление закупками государственными автономными и бюджетными учреждениями
Управление закупками государственными автономными и бюджетными учреждениями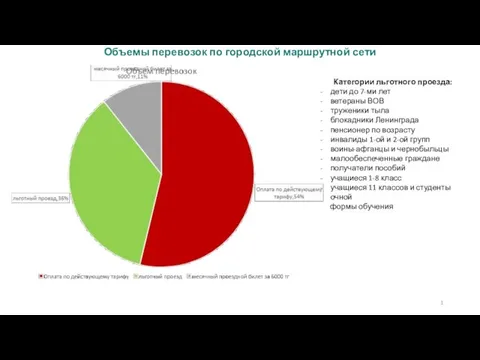 Объемы перевозок по городской маршрутной сети
Объемы перевозок по городской маршрутной сети Виды заданий ЕГЭ
Виды заданий ЕГЭ Nineteeneffect by nineteenstudio
Nineteeneffect by nineteenstudio Буслаев Федор Иванович
Буслаев Федор Иванович Основы психологии. 8 класс
Основы психологии. 8 класс Судебная система
Судебная система Культуризм или бодибилдинг
Культуризм или бодибилдинг