Презентация на тему Теоремы синусов и косинусов 9 КЛАСС

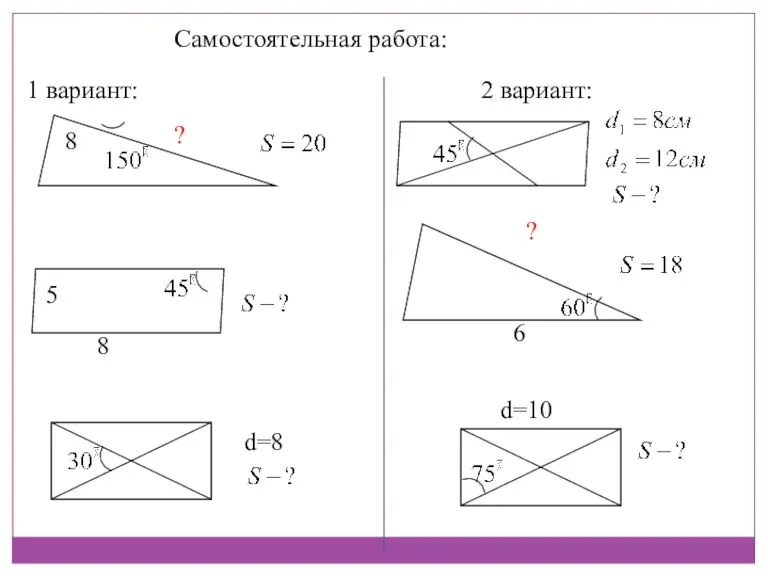
Самостоятельная работа:
1 вариант:
2 вариант:
8
?
8
5
d=8
?
6
d=10

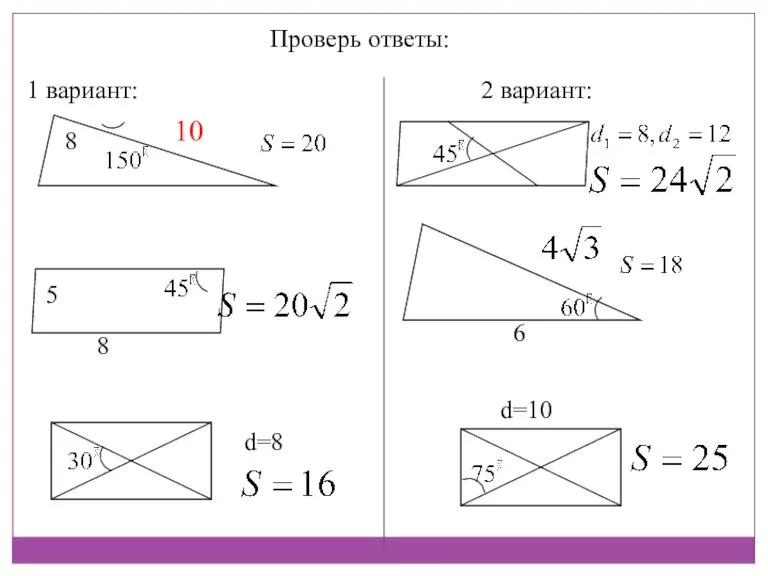
Проверь ответы:
1 вариант:
2 вариант:
8
10
8
5
d=8
6
d=10

ТЕОРЕМА КОСИНУСОВ.
ИСТОРИЯ.
Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» Евклида.

ТЕОРЕМА КОСИНУСОВ.
ИСТОРИЯ.
Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал Региомонтан, назвав её «теоремой Альбатегния» (по имени ал-Баттани).

ТЕОРЕМА КОСИНУСОВ.
ИСТОРИЯ.
В Европе теорему косинусов популяризовал Франсуа Виет в XVI столетии. В начале XIX столетия её стали записывать в принятых по сей день алгебраических обозначениях.

A
B
C
Теорема косинусов:
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними
а
с
b

ТЕОРЕМА СИНУСОВ.
ИСТОРИЯ.
Самое древнее доказательство для теоремы синусов на плоскости описано в книге Насир ад-Дин Ат-Туси «Трактат о полном четырёхстороннике» написанной в XIII веке. Теорема синусов для сферического треугольника была доказана математиками средневекового Востока ещё в X веке. В труде Ал-Джайяни XI века «Книга о неизвестных дугах сферы» приводилось общее доказательство теоремы синусов на сфере
Насир ад-Дин Ат-Туси

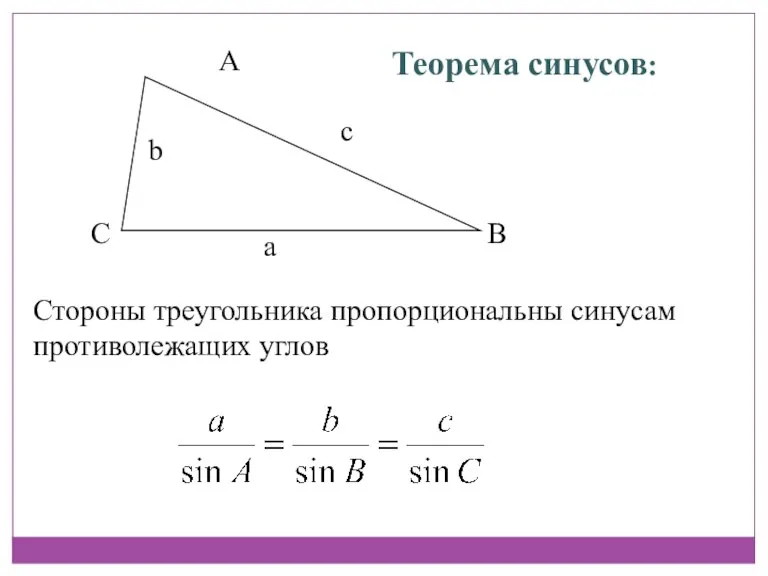
A
B
C
Теорема синусов:
Стороны треугольника пропорциональны синусам противолежащих углов
а
с
b

ТЕОРЕМА СИНУСОВ
Замечание: Можно доказать, что отношение стороны треугольника к синусу противолежащего угла равно диаметру описанной окружности. Следовательно, для любого треугольника ABC со сторонами AB=c, BC=a, CA=b имеют место равенства
Где R – радиус описанной окружности.

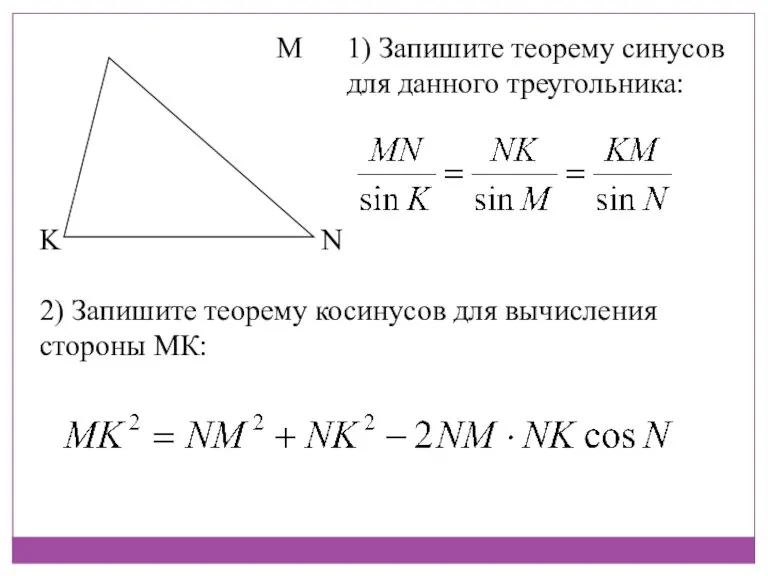
M
N
K
1) Запишите теорему синусов для данного треугольника:
2) Запишите теорему косинусов для вычисления стороны МК:

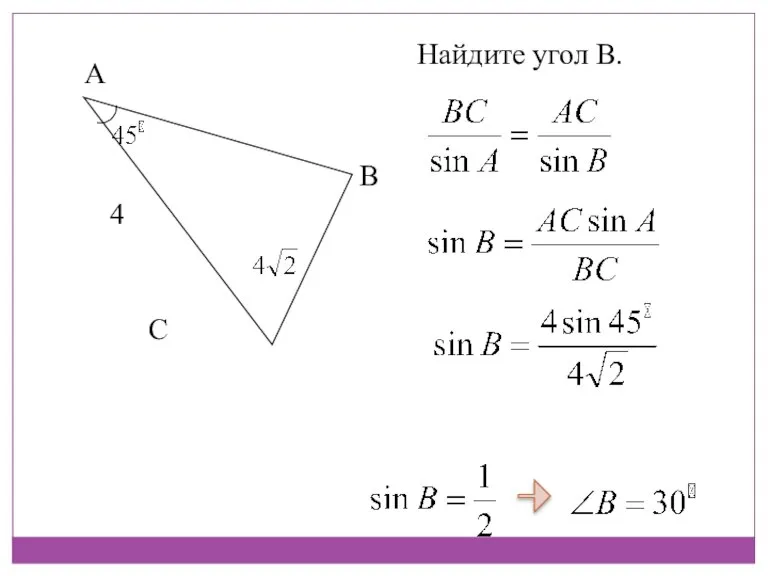
Найдите угол В.

Найдите длину стороны ВС.
А
С
В
3

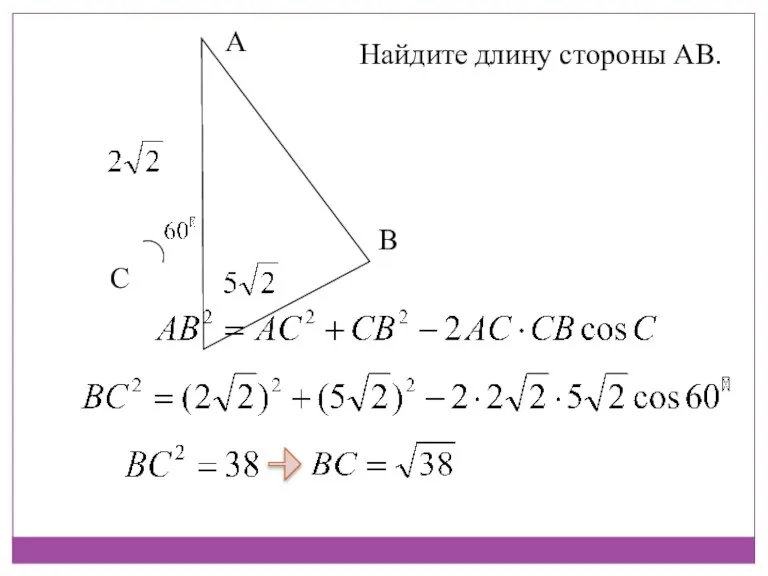
Найдите длину стороны АВ.
А
С
В

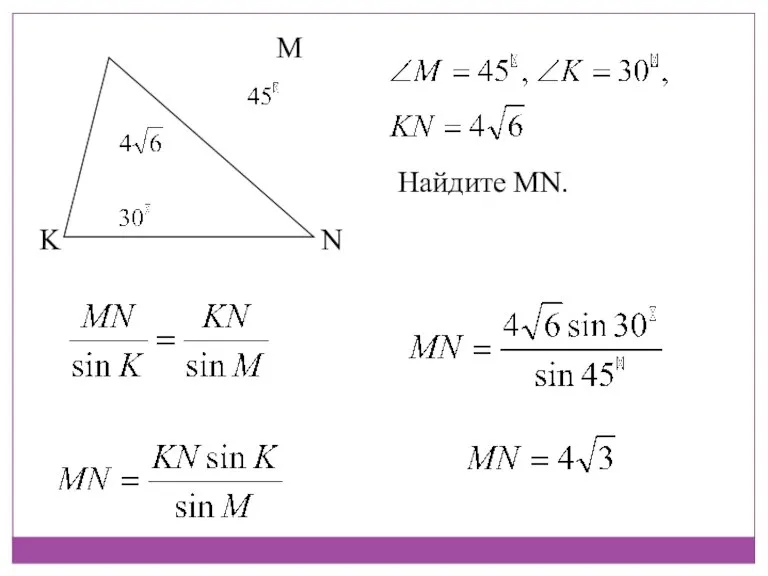
M
N
K
Найдите MN.

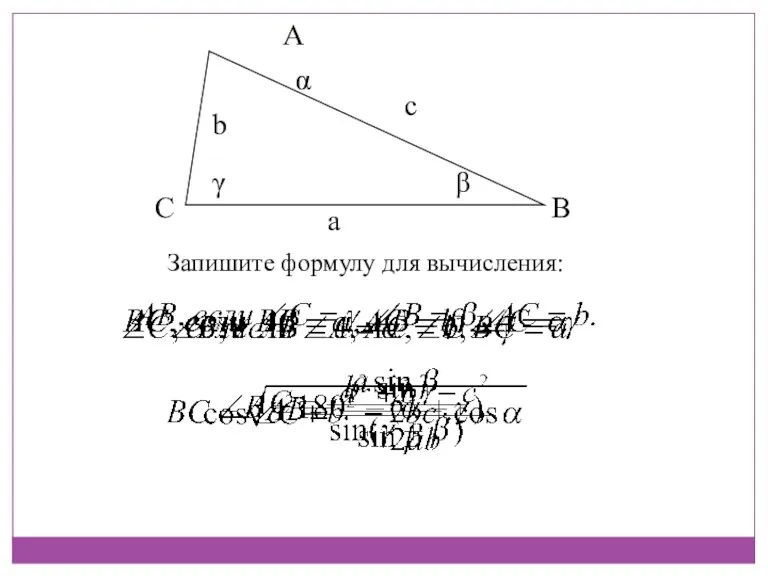
Запишите формулу для вычисления: