Слайд 2Краткая аннотация
В работе указаны три способа задания кривых линий. Приведены примеры

кривых линий. При написании работы применялись, в большинстве своем, теоретические методы исследования: изучение литературы, анализ и систематизация полученной информации, построение кривых.
Слайд 3
Актуальность
Кривые линии повсеместно встречаются в окружающем нас мире. В нашей повседневной

жизни мы постоянно сталкиваемся с огромным количеством кривых линий, которые порой не замечаем. Если бы в мире не было кривых линий, то все предметы были бы угловатыми, квадратными. И вещи, имеющие мягкие очертания, приятны для восприятия зрительными органами человека. Даже в природе количество n-угольных предметов сведено к минимуму.
Слайд 4Проблема
С помощью линий удаётся решать многие научные и
инженерные задачи, но

решение которых аналитическим путём часто приводит к использованию чрезвычайно громоздкого математического аппарата.
Слайд 5Исследованием кривых линий занимались:
Блэз Паскаль
Blaise Pascal
(19.06.1623 – 19.08.1662)
Один из самых знаменитых

людей в истории человечества. Паскаль умер, когда ему было 39 лет, но, несмотря на столь короткую жизнь, вошел в историю как выдающийся математик, физик, философ и писатель. Его именем названы единица давления (паскаль) и весьма популярный сегодня язык программирования.
Слайд 6Дезарг Жерар [1593, Лион, — 1662, там же (по др. данным —

1591—1661)], французский математик. Был военным инженером. Заложил основы проективной и начертательной геометрии. В своих исследованиях систематически применял перспективное изображение. Первым ввёл в геометрию Бесконечно удалённые элементы.
Слайд 7Цель работы
Изучить виды основных, наиболее известных кривых линий и их основные

свойства. Научится строить различные кривые. Найти оптимальные способы построения кривых линий.
Слайд 8Задачи:
1. Проанализировать литературу.
2. Просмотреть интернет ресурсы.
3. Определить способы.
4. Сравнить способы задания кривых.
5.

Оценить.
Слайд 9Способы задания кривых
Существует 3 способа задания кривых.
· аналитический
· графический
· табличный

Слайд 10Аналитический способ
Аналитический- кривая задана математическим уравнением.
Чаще всего закон, устанавливающий связь между аргументом

и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа — основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Слайд 11Графический способ
Графический- кривая задана визуально на носителе графической информации.
Графический способ. Графиком функции

y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Слайд 12Табличный способ
Табличный- кривая задана координатами последовательного ряда точек.
Табличный способ. Довольно распространенный, заключается

в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Слайд 13Плоские кривые линии
Существуют ПЛОСКИЕ КРИВЫЕ ЛИНИИ Кривые линии, все точки которых принадлежат

одной плоскости, называются плоскими.
Порядок плоской алгебраической кривой линии определяется наибольшим числом точек её пересечения прямой линией. Любая прямая линия может пересекать алгебраическую кривую линию n-го порядка не более, чем в n точках.
Рассмотрим несколько примеров алгебраической кривой линии:
Слайд 14Парабола
Парабола – кривая второго порядка, прямая пересекает ее в двух точках. При

этом парабола может быть определена как:
-множество точек М(A,B,C,...) плоскости, расстояние которых до определенной точки F этой плоскости (фокуса параболы) равно расстоянию до определенной прямой DD1 - директрисы параболы;
-линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и параллельная какой либо касательной плоскости этого конуса;
-в прямоугольной системе координат 0ху с началом в вершине параболы и осью 0х направленной по оси параболы уравнение параболы имеет так называемый канонический вид
Слайд 15Гипербола
. Гипербола :
- множество точек М(A,B,C,...) плоскости, разность (по абсолютной величине) расстояний

которых до двух определенных точек F и F1 этой плоскости (фокусов гиперболы) величина постоянная:
FM - F1M=2а<2с
Середина 0 отрезка FF1 (фокусного расстояния) называется центром гиперболы;
- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающая обе его полости;
- в прямоугольной системе координат 0ху с началом в центре гиперболы, на оси 0х которой лежат фокусы гиперболы уравнение гиперболы имеет так называемый канонический вид
где а и b длины полуосей гиперболы.
Слайд 16Эллипс
. Эллипс :
- множество точек М(xy) плоскости, сумма расстояний МF1 и МF2
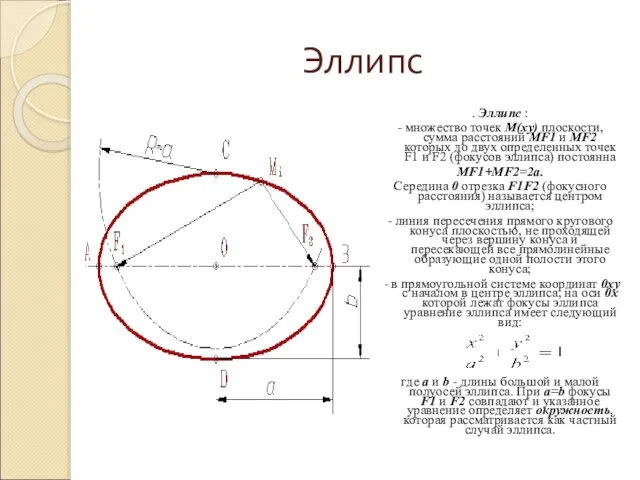
которых до двух определенных точек F1 и F2 (фокусов эллипса) постоянна
МF1+МF2=2а.
Середина 0 отрезка F1F2 (фокусного расстояния) называется центром эллипса;
- линия пересечения прямого кругового конуса плоскостью, не проходящей через вершину конуса и пересекающей все прямолинейные образующие одной полости этого конуса;
- в прямоугольной системе координат 0ху с началом в центре эллипса, на оси 0х которой лежат фокусы эллипса уравнение эллипса имеет следующий вид:
где а и b - длины большой и малой полуосей эллипса. При а=b фокусы F1 и F2 совпадают и указанное уравнение определяет окружность, которая рассматривается как частный случай эллипса.
Слайд 17Кривые конических сечений
Все, рассмотренные плоские кривые линии можно получить как линии пересечения

поверхности прямого кругового конуса с плоскостями, различно расположенными по отношению к оси конуса. Поэтому эти кривые называют кривыми конических сечений.
Трансцендентные кривые в отличие от алгебраических могут иметь бесконечное количество точек пересечения с прямой, точек перегиба, вершин и т.п.
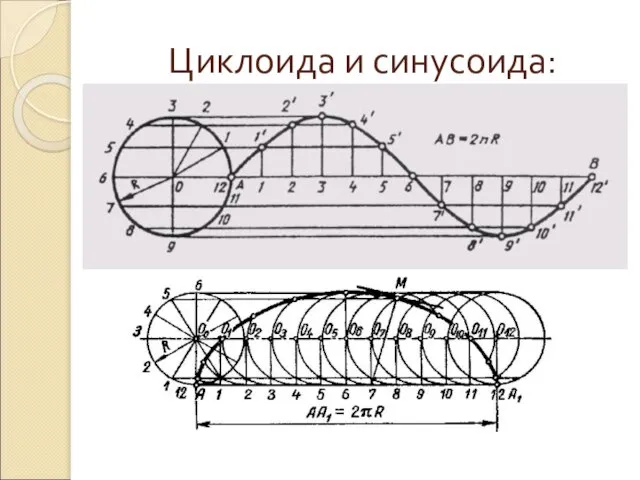
Слайд 18Синусоида
Синусоида - график функции у=sin x, непрерывная кривая линия с периодом
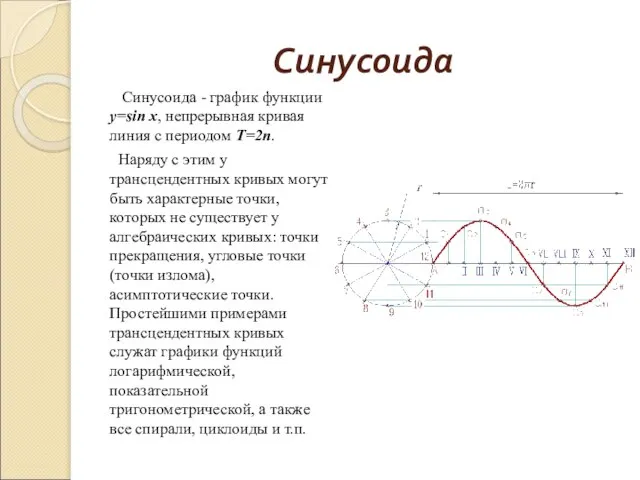
Т=2п.
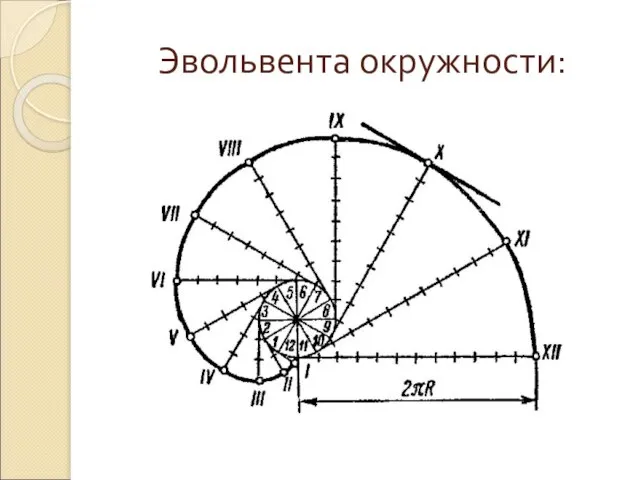
Наряду с этим у трансцендентных кривых могут быть характерные точки, которых не существует у алгебраических кривых: точки прекращения, угловые точки (точки излома), асимптотические точки. Простейшими примерами трансцендентных кривых служат графики функций логарифмической, показательной тригонометрической, а также все спирали, циклоиды и т.п.
Слайд 19Рассмотрим несколько примеров графической кривой линии:
Эллипс
Эллипс представляет собой замкнутую плоскую кривую
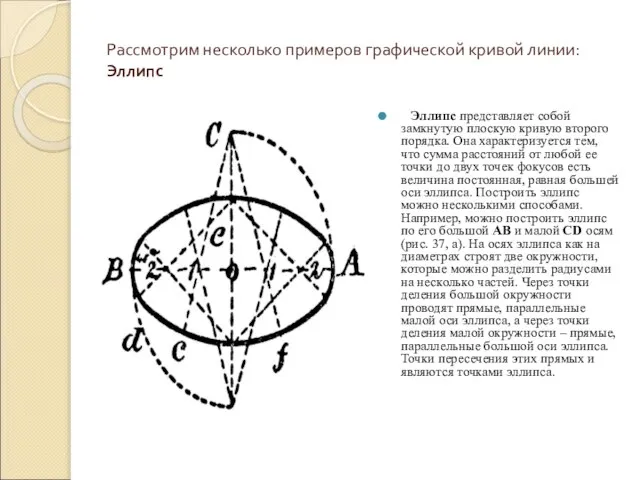
второго порядка. Она характеризуется тем, что сумма расстояний от любой ее точки до двух точек фокусов есть величина постоянная, равная большей оси эллипса. Построить эллипс можно несколькими способами. Например, можно построить эллипс по его большой АВ и малой CD осям (рис. 37, а). На осях эллипса как на диаметрах строят две окружности, которые можно разделить радиусами на несколько частей. Через точки деления большой окружности проводят прямые, параллельные малой оси эллипса, а через точки деления малой окружности – прямые, параллельные большой оси эллипса. Точки пересечения этих прямых и являются точками эллипса.
Слайд 20Приемы построения параболы и гиперболы:
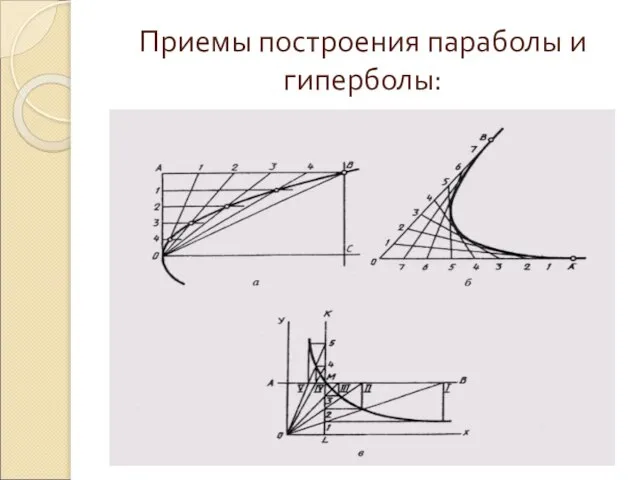
Слайд 23Выводы
Каждый из предложенных способов имеет свои преимущества и недостатки, поэтому выбор

способа построения кривых линий зависит от конкретной поставленной задачи.
Изучение кривых второго порядка дало толчок развитию теорий алгебраических и механических кривых: лемнискаты, конхоиды, циклоиды, эпициклоиды, гипоциклоиды, кардиоиды и т.д. Изучение этих кривых, их свойств могут вылиться в интересные ученические исследовательские работы.




















 Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Информационное оснащение женских консультаций
Информационное оснащение женских консультаций Презентация на тему Сложение чисел с помощью координатной прямой
Презентация на тему Сложение чисел с помощью координатной прямой  Что такое натуральные ткани? каковы их свойства?
Что такое натуральные ткани? каковы их свойства? Неорганические кислоты
Неорганические кислоты Фторхинолоны клиническая фармакология иособенности действия
Фторхинолоны клиническая фармакология иособенности действия ИГРА С БУДУЩИМ
ИГРА С БУДУЩИМ Антонио Гауди - великий архитектор
Антонио Гауди - великий архитектор Сообщающиеся сосуды
Сообщающиеся сосуды Плавание тел
Плавание тел Любимые места отдыха
Любимые места отдыха Повседневная жизнь земледельцев и горожан в средние века
Повседневная жизнь земледельцев и горожан в средние века Сводный медиаплан рекламной кампании
Сводный медиаплан рекламной кампании Лагерь молодёжного актива
Лагерь молодёжного актива Повесть Н.С.Лескова «Очарованный странник»
Повесть Н.С.Лескова «Очарованный странник» Мельник М.В. Управление риском
Мельник М.В. Управление риском Ошибки вокруг нас
Ошибки вокруг нас Приблизительные размеры территорий
Приблизительные размеры территорий Chanel SS21. Alberta Ferretti SS21. Вдохновение
Chanel SS21. Alberta Ferretti SS21. Вдохновение Обязательные условия при сканировании
Обязательные условия при сканировании chekhov
chekhov Презентация на тему Происхождение рас
Презентация на тему Происхождение рас  Обзор Информационно-аналитической системы «Семантический архив» 3.0
Обзор Информационно-аналитической системы «Семантический архив» 3.0 ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ»
ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ» Презентация на тему Памятник русскому солдату в Болгарии
Презентация на тему Памятник русскому солдату в Болгарии Как маркетинговая аналитика увеличивает продажи. Часть 1
Как маркетинговая аналитика увеличивает продажи. Часть 1 აუდიტი გამა
აუდიტი გამა Изделия из бересты
Изделия из бересты