Содержание
- 2. Содержание Введение. Основная часть Глава 1. Определение вневписанной окружности. Центр вневписанной окружности. Касательная к вневписанной окружности.
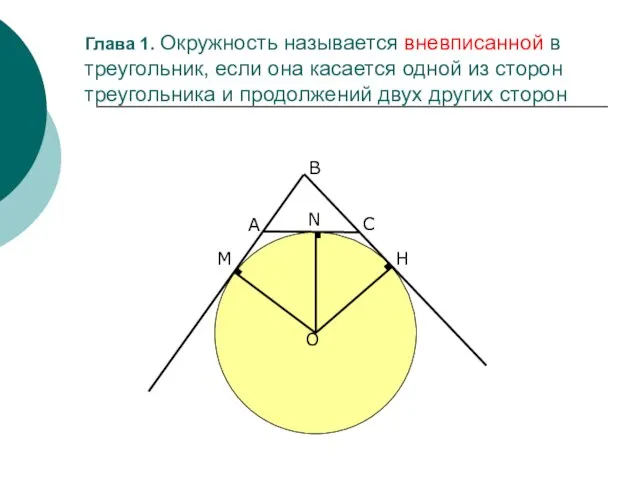
- 3. Глава 1. Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника и продолжений
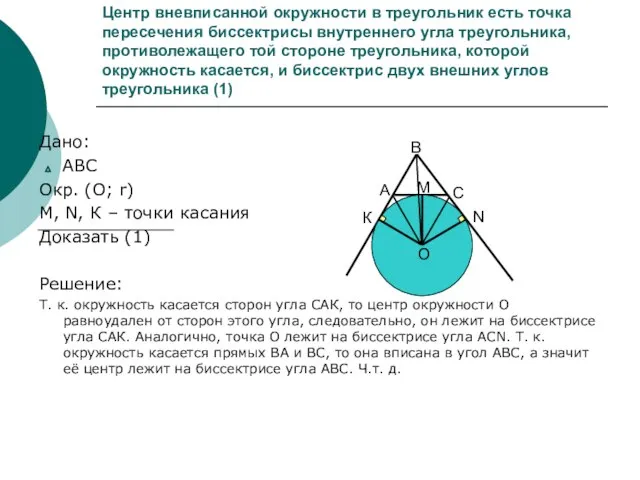
- 4. Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника,
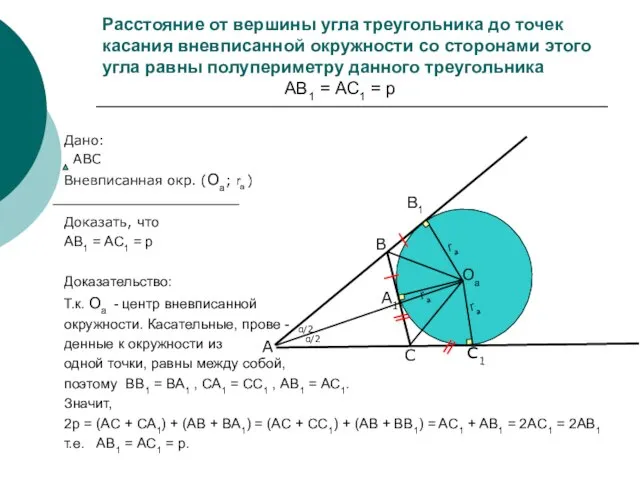
- 5. Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру
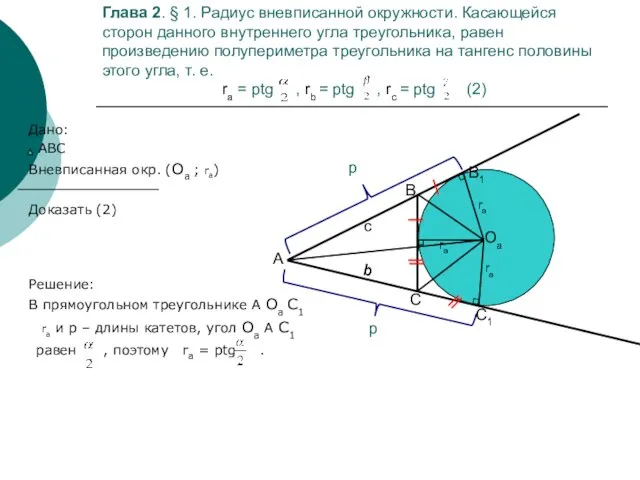
- 6. Глава 2. § 1. Радиус вневписанной окружности. Касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра
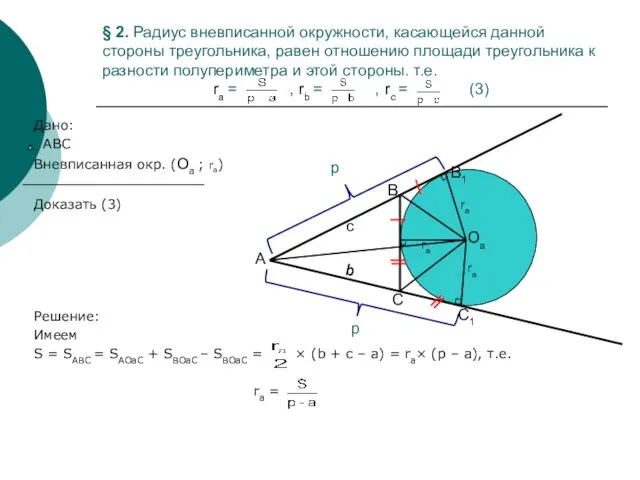
- 7. § 2. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра
- 8. Глава 3. § 1 Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра
- 9. § 2. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е.
- 10. § 3. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е. rarb
- 11. § 4. Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра
- 12. Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е.
- 13. Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса
- 14. § 5. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам
- 16. Скачать презентацию








 Архитектура и живопись русского классицизма
Архитектура и живопись русского классицизма О ВЛИЯНИИ ЭКСПЕРИМЕНТАЛЬНЫХ УСТРОЙСТВ НА ФИЗИКУ И БЕЗОПАСНОСТЬ ИССЛЕДОВАТЕЛЬСКИХ РЕАКТОРОВ XIII ЕЖЕГОДНОЕ РОССИЙСКОЕ СОВЕЩАНИЕ «
О ВЛИЯНИИ ЭКСПЕРИМЕНТАЛЬНЫХ УСТРОЙСТВ НА ФИЗИКУ И БЕЗОПАСНОСТЬ ИССЛЕДОВАТЕЛЬСКИХ РЕАКТОРОВ XIII ЕЖЕГОДНОЕ РОССИЙСКОЕ СОВЕЩАНИЕ « Нанотехнологии - инвестиционный ресурс развития Удмуртской Республики
Нанотехнологии - инвестиционный ресурс развития Удмуртской Республики Правила санитарии, гигиены и безопасной работы
Правила санитарии, гигиены и безопасной работы Система аварийного ввода бора (СБВБ) на АЭС
Система аварийного ввода бора (СБВБ) на АЭС История эволюционных идей. Карл Линней
История эволюционных идей. Карл Линней Формирование исполнительского мастерства в условиях образовательной среды в ДШИ
Формирование исполнительского мастерства в условиях образовательной среды в ДШИ Документация как информационное обеспечение бухгалтерского учета
Документация как информационное обеспечение бухгалтерского учета Современная научная космология.
Современная научная космология. Расписание дня школьника
Расписание дня школьника Перспективы развития мультимодальных грузовых перевозок в Ульяновской области
Перспективы развития мультимодальных грузовых перевозок в Ульяновской области Почему невозможно утонуть в грязевом вулкане?
Почему невозможно утонуть в грязевом вулкане? Лекция 3Показатели энергосбережения и повышения энергетической эффективности
Лекция 3Показатели энергосбережения и повышения энергетической эффективности Образец бренда
Образец бренда Летняя оздоровительная кампания 2010год
Летняя оздоровительная кампания 2010год Компания Xerographic Print Service основана в 1994 г.в Нидерландах. Производственные филиалы работают в странах ЕС и Китае.
Компания Xerographic Print Service основана в 1994 г.в Нидерландах. Производственные филиалы работают в странах ЕС и Китае. Функциональное зонирование участка
Функциональное зонирование участка Һөйләмдең баш һәм эйәрсән киҫәктәре
Һөйләмдең баш һәм эйәрсән киҫәктәре Презентация на тему Поздравление с Новым годом
Презентация на тему Поздравление с Новым годом УМК для начальной школы
УМК для начальной школы Методическое объединение педагогов дополнительного образования и учителей художественно-эстетического цикла
Методическое объединение педагогов дополнительного образования и учителей художественно-эстетического цикла ЭКОЛОГ - Профессия XXI века?
ЭКОЛОГ - Профессия XXI века? Система контроля безопасности СКБ Dog
Система контроля безопасности СКБ Dog Детальный Углеводородный Анализ продуктов первичной переработки нефти, продуктов риформинга, готовой продукции
Детальный Углеводородный Анализ продуктов первичной переработки нефти, продуктов риформинга, готовой продукции Рекреационные ресурсы Луганщины
Рекреационные ресурсы Луганщины Filippovich_i_Bashkatova_1
Filippovich_i_Bashkatova_1 12 Декабря - День Конституции Российской Федерации
12 Декабря - День Конституции Российской Федерации Естественнонаучный турнир
Естественнонаучный турнир