Содержание
- 2. Признаки делимости числа по последней цифре данного числа. ( на 2, на 5, на10)
- 3. Для того, чтобы число делилось на 2, необходимо и достаточно, чтобы последняя цифра была четной. Пример:
- 4. Признак делимости на 5: Для того, чтобы число делилось на 5, необходимо и достаточно, чтобы оно
- 5. Признаки делимости на 10 Для того, чтобы число делилось на 10, необходимо, чтобы оно оканчивалось на
- 6. Признаки делимости числа, по двух последним цифрам данного числа. (на 4 и на 25 , 50)
- 7. Признаки делимости на 4 Число делится на 4 если делится на 4 число, составленное из двух
- 8. Признаки делимости на 25 Число делится на 25, если делится на 25 число, составленное из двух
- 9. Признаки делимости на 50 Если в конце числа два нуля или 50 , то данное число
- 10. Признаки делимости числа, по сумме цифр данного числа. ( на 3 и на 9)
- 11. Признак делимости на 3 Для того, чтобы число делилось на 3 , необходимо и достаточно, чтобы
- 12. Признак делимости на 9 Для того, чтобы число делилось на 9, необходимо и достаточно, чтобы сумма
- 13. Признаки делимости на 8: ( по трем последним цифрам) Для того, чтобы число делилось на 8,
- 14. Получили признаки делимости на : 2. 3, 4, 5, 8, 9, 1 0, 25, 50. Составляя
- 15. Если число А = m* n, где m, n взаимно простые, то число В делится на
- 16. Признаки делимости на 7: Для того, чтобы число делилось на 7, надо: 1.Число, стоящее до десятков,
- 17. Признаки делимости на 11: Для того, чтобы число делилось на 11, необходимо, чтобы разность между суммой
- 18. Признак делимости на 13 Число делится на 13 тогда, когда число его десятков, сложенное с учетверённым
- 19. Признаки делимости на 17 Для того, чтобы число делилось на 17, необходимо, чтобы число его десятков,
- 20. Признаки делимости на 19: Для того, чтобы число делилось на 19 необходимо и достаточно, чтобы число
- 21. Признак делимости на 23: Для того, чтобы число делилось на 23, необходимо, чтобы число его сотен,
- 22. Спасибо за участие
- 24. Скачать презентацию





















 Личность и ее социализация
Личность и ее социализация Власть и народ в стихотворении Н.А. Некрасова «Железная дорога»
Власть и народ в стихотворении Н.А. Некрасова «Железная дорога» Гордость и эгоизм
Гордость и эгоизм Паустовский Константин Сергеевич (3 класс)
Паустовский Константин Сергеевич (3 класс)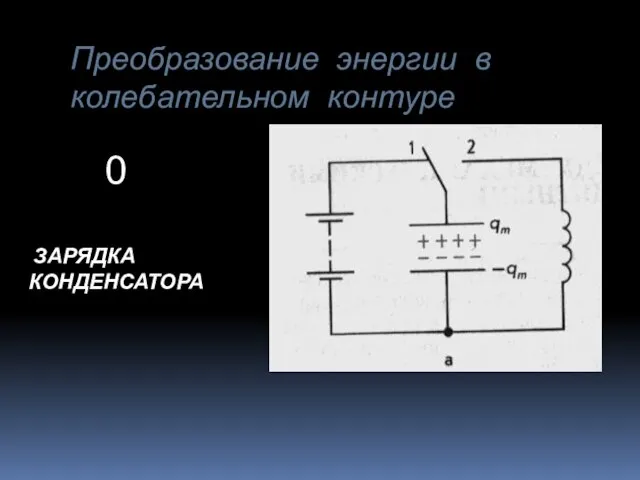 Презентация на тему Преобразование энергии в колебательном контуре
Презентация на тему Преобразование энергии в колебательном контуре  Слова благодарности выпускников учителям и родителям
Слова благодарности выпускников учителям и родителям МЕТОДЫ ОБУЧЕНИЯ
МЕТОДЫ ОБУЧЕНИЯ Основные ошибки при подаче документов на лицензирование
Основные ошибки при подаче документов на лицензирование Молодежная музыкальная Культура
Молодежная музыкальная Культура Дизайн вещно-пространственной среды жилища
Дизайн вещно-пространственной среды жилища Тутанхамон
Тутанхамон Ответственные родители
Ответственные родители Паттерн «Specification»
Паттерн «Specification» Композитинг
Композитинг ОСНОВНЫЕ ЦЕННОСТИ БРЕНДА «ТОРЭКС»
ОСНОВНЫЕ ЦЕННОСТИ БРЕНДА «ТОРЭКС» План Путина – победа России
План Путина – победа России Генрих Гейне (13 декабря 1797 -17 февраля 1856)
Генрих Гейне (13 декабря 1797 -17 февраля 1856) НАШИ РЕСУРСЫ РАЗВИТИЯ
НАШИ РЕСУРСЫ РАЗВИТИЯ Герои войны - дети
Герои войны - дети Коммерческая деятельность
Коммерческая деятельность My Trip to the UK
My Trip to the UK Мотивация кураторов и старших операторов
Мотивация кураторов и старших операторов Психологическая готовность детей к школе
Психологическая готовность детей к школе Компетенции сотрудников в краткосрочном проекте
Компетенции сотрудников в краткосрочном проекте Доступный спорт на открытом воздухе для жителей Старой Ржевки
Доступный спорт на открытом воздухе для жителей Старой Ржевки API WebMoney Transfer Для интернет-проектов. WebMoney как провайдер идентификации -11 млн зарегистрированных клиентов; - 4 уровня аттестации; - авт
API WebMoney Transfer Для интернет-проектов. WebMoney как провайдер идентификации -11 млн зарегистрированных клиентов; - 4 уровня аттестации; - авт НОРМЫ ПОВЕДЕНИЯ
НОРМЫ ПОВЕДЕНИЯ Зимний пейзаж
Зимний пейзаж