Содержание
- 2. Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому
- 3. Представление левой части неравенства в виде суммы неотрицательных слагаемых (правая часть равна 0) с использованием тождеств.
- 4. для любых действительных х и у Пример 2. Доказать, что для любых x и y Доказательство.
- 5. 2. Метод от противного Вот хороший пример применения данного метода. Доказать, что для a, b ϵ
- 6. Пример 5. Доказать, что для любых чисел А,В,С справедливо неравенство Доказательство. Очевидно, что данное неравенство достаточно
- 7. Пусть теперь нашлись такие неотрицательные числа А, В и С, для которых выполняется неравенство , что
- 8. для хϵR для хϵR Использование свойств квадратного трехчлена Метод основан на свойстве неотрицательности квадратного трехчлена ,
- 9. для хϵR Пример 7. Доказать, что для любых действительных х и у имеет место быть неравенство
- 10. Пример 8. Доказать, что для любых действительных значениях х и у. Доказательство. Пусть , Это означает,
- 11. Метод введения новых переменных или метод подстановки Пример 9. Доказать, что для любых неотрицательных чисел х,
- 12. для аϵR Использование свойств функций. Пример 10. Докажем неравенство для любых а и b. Доказательство. Рассмотрим
- 13. Пример 11. Докажем, что для любых Доказательство. на R. Если , то знаки чисел и совпадают,
- 14. Применение метода математической индукции Данный метод применяется для доказательства неравенств относительно натуральных чисел. Пример 12. Доказать,
- 15. *3 3) Докажем истинность утверждения при n=k+1. Сравним и : , Имеем: Вывод: утверждение верно для
- 16. Использование замечательных неравенств Теорема о средних (неравенство Коши) Неравенство Коши – Буняковского Неравенство Бернулли Рассмотрим каждое
- 17. Применение теоремы о средних (неравенства Коши) Среднее арифметическое нескольких неотрицательных чисел больше или равно их среднего
- 18. Пусть n=2, , , тогда Пусть n=2, a>0, тогда Пусть n=3, , , , тогда Пример
- 19. Неравенство Коши - Буняковского Неравенство Коши - Буняковского утверждает, что для любых ; справедливо соотношение Доказанное
- 20. Пример 14. Доказать, что для любых a,b,c ϵ R справедливо неравенство Доказательство. Запишем исследуемое неравенство в
- 21. Неравенство Бернулли Неравенство Бернулли утверждает, что если х>-1, то для всех натуральных значений n выполняется неравенство
- 22. Пример 16. Доказать, что для любых n ϵ N Доказательство. Положив х=0,5 и применив теорему Бернулли
- 24. Скачать презентацию





















 Патент
Патент Концертный зал Кубанского казачьего хора
Концертный зал Кубанского казачьего хора Презентация на тему Внешняя политика Ивана Грозного
Презентация на тему Внешняя политика Ивана Грозного  А Где тут Дед Мороз
А Где тут Дед Мороз Разность квадратов
Разность квадратов Итоги работы Центров здоровья в городе Новосибирске за 5 месяцев 2010 года
Итоги работы Центров здоровья в городе Новосибирске за 5 месяцев 2010 года Электричество в жизни
Электричество в жизни КОМПЬЮТЕРНАЯ ГРАФИКА
КОМПЬЮТЕРНАЯ ГРАФИКА Преемственность в развитии социальной компетентности дошкольников и младших школьников
Преемственность в развитии социальной компетентности дошкольников и младших школьников Башнефтегеофизика
Башнефтегеофизика МДОУ «Староахпердинский детский сад «Родник» Батыревского района Чувашской республики
МДОУ «Староахпердинский детский сад «Родник» Батыревского района Чувашской республики Все работы хороши, выбирай на вкус
Все работы хороши, выбирай на вкус ОТ БУКВЫ – К СМЫСЛУ СЛОВА
ОТ БУКВЫ – К СМЫСЛУ СЛОВА Основы финансового моделирования
Основы финансового моделирования Использование современных информационных и коммуникационных технологий в образовании
Использование современных информационных и коммуникационных технологий в образовании Растения в школе-
Растения в школе- Ресторан-бар Route 148 для банкетов
Ресторан-бар Route 148 для банкетов Тема 16
Тема 16 Die Reise nach Deutschland
Die Reise nach Deutschland Введение в экологию. Экологические факторы. Сообщества. Экосистемы
Введение в экологию. Экологические факторы. Сообщества. Экосистемы Моря, озера и реки России (4 класс)
Моря, озера и реки России (4 класс) Теремок
Теремок Семейные конфликты
Семейные конфликты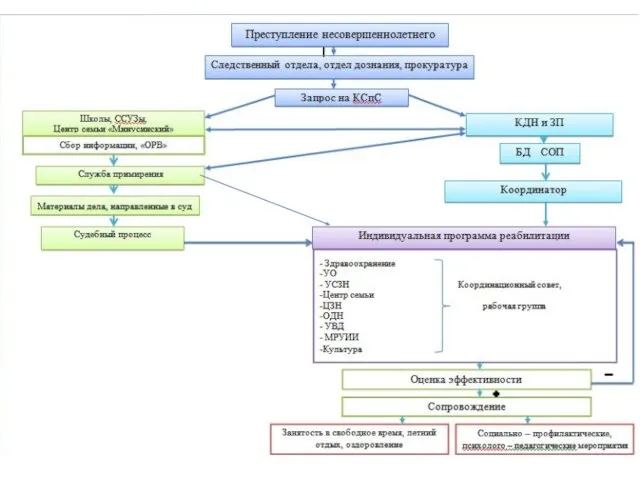 КАРТА социально - психологического сопровождения несовершеннолетних правонарушителей Ф.И.О. правонарушителя Дата рождения Домаш
КАРТА социально - психологического сопровождения несовершеннолетних правонарушителей Ф.И.О. правонарушителя Дата рождения Домаш Механическая картина мира
Механическая картина мира 里边 面
里边 面 Страны мира
Страны мира Овощеводство и плодоводство
Овощеводство и плодоводство