Содержание
- 2. Метод Гаусса решения СЛАУ. Модификации. Варианты распараллеливания Докладчик: Кожухов А.Е.
- 3. ОБЩИЕ ПОНЯТИЯ
- 4. Задание СЛАУ или
- 5. При матричном задании СЛАУ имеют место обозначения: А – матрица коэффициентов системы; b – вектор свободных
- 6. Задачи, сводимые к решению СЛАУ К решению систем линейных алгебраических уравнений сводимы задачи из многих областей
- 7. Особенности постановки задач: являются конечно–разностными или конечно–элементными моделями; задаются дифференциальными уравнениями с начальными или краевыми условиями.
- 8. Классы методов решения СЛАУ Прямые методы: а) метод Холесского для плотных матриц; б) метод Холесского для
- 9. Итерационные методы: а) метод Якоби; б) метод Гаусса–Зейделя; в) метод сопряжённых градиентов; г) метод последовательной верхней
- 10. МЕТОД ИСКЛЮЧЕНИЯ ПЕРЕМЕННЫХ ГАУССА
- 11. Шаг прямого хода Деление коэффициентов текущего уравнения на коэффициент при исключаемой переменной:
- 12. Шаг прямого хода Для всех уравнений со 2–ого по n–ое выполнить действия: умножение обеих частей 1–ого
- 13. Из уравнений со 2–ого по n–ое можно составить эквивалентную исходной систему уравнений, но с количеством неизвестных
- 14. Результат выполнения прямого хода метода Гаусса …
- 15. Обратный ход метода Гаусса – вычисление значений переменных, начиная с xn до x1.
- 16. МОДИФИКАЦИИ МЕТОДА ГАУССА
- 17. Метод Гаусса в матричной форме Пусть задана исходная система уравнений. Тогда на исключение неизвестной xi из
- 18. Метод Гаусса в матричной форме
- 19. Метод Гаусса в матричной форме
- 21. Скачать презентацию


















 Вредные привычки и их влияние на здоровье
Вредные привычки и их влияние на здоровье Публичный доклад муниципальногобюджетного дошкольного образовательного учреждения
Публичный доклад муниципальногобюджетного дошкольного образовательного учреждения Виды шовного материала и требования применяемые к нему
Виды шовного материала и требования применяемые к нему Великие математики и их исследования
Великие математики и их исследования Комрьютер
Комрьютер Особенности архитектуры
Особенности архитектуры Бизнес-план: открытие компьютерного клуба
Бизнес-план: открытие компьютерного клуба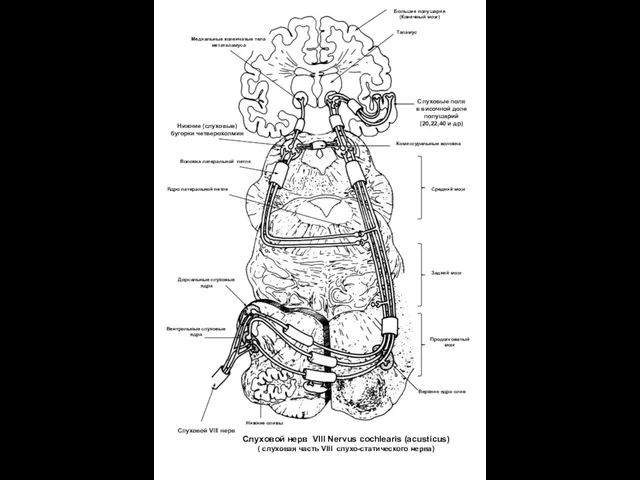 Слуховой нерв
Слуховой нерв  FILOSOFIYa_I_NAUKA (2)
FILOSOFIYa_I_NAUKA (2) Наука и искусство
Наука и искусство Тайны метафоры
Тайны метафоры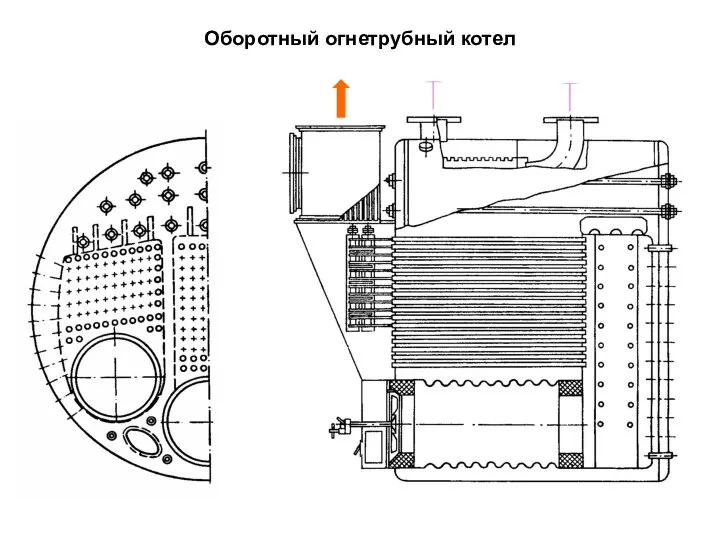 Оборотный огнетрубный котел
Оборотный огнетрубный котел Презентация на тему Известняк (4 класс)
Презентация на тему Известняк (4 класс) Стальные тигры. Специальная команда
Стальные тигры. Специальная команда Ядерное, химическое и биологическое оружие
Ядерное, химическое и биологическое оружие Мини-энциклопедия ПК
Мини-энциклопедия ПК Love&Faith. Письма о любви
Love&Faith. Письма о любви Центральные и вписанные углы
Центральные и вписанные углы По Ипотеке
По Ипотеке Художники Сенгилеевского района
Художники Сенгилеевского района Мавзолей в Агре Тадж Махал
Мавзолей в Агре Тадж Махал Педсовет
Педсовет Презентация на тему Проблемы подросткового возраста и пути их преодоления
Презентация на тему Проблемы подросткового возраста и пути их преодоления Презентация на тему Последствия парникового эффекта для Земли
Презентация на тему Последствия парникового эффекта для Земли  День 1-й. АстроМагия – проработка гороскопа
День 1-й. АстроМагия – проработка гороскопа Московский Государственный Университет им. М.В. Ломоносовафизический факультет
Московский Государственный Университет им. М.В. Ломоносовафизический факультет Веселая переменка
Веселая переменка Межрегиональные стажировки: эффективный обмен опытом, внедрение интерактивных методов обучения
Межрегиональные стажировки: эффективный обмен опытом, внедрение интерактивных методов обучения