Слайд 2Введение.
В мире не происходит ничего, в чем не был бы виден смысл

какого-нибудь максимума или минимума. Л. Эйлер.
Слайд 3Введение.
Решая некоторые задачи, я встретил такие понятия, как «наибольшее значение», «наименьшее значение»,

«выгодное», «наилучшее», и меня заинтересовало решение таких задач. Оказывается, что в математике исследование задач на максимум и минимум началось очень давно – двадцать пять веков назад. Долгое время к задачам на отыскание экстремумов (с лат. «экстремум» – «крайний») не было единых подходов.
Слайд 4Введение.
Но примерно триста лет назад – были созданы первые общие методы решения

и исследования задач на экстремумы. Тогда же выяснилось, что некоторые специальные задачи оптимизации играют очень важную роль в естествознании. Задачи на максимум и минимум на протяжении всей истории математики играли важную роль в развитии этой науки.
Слайд 5Введение.
За всё это время накопилось большое число красивых, важных, ярких и интересных

задач в геометрии алгебре и других науках. В решении конкретных задач принимали участие крупнейшие учёные прошлых эпох: Евклид, Архимед, Аполлоний, Герон, Торричелли, Иоганн и Якоб Бернулли, Исаак Ньютон и многие другие. Решение конкретных задач стимулировало развитие теории, и в итоге были выработаны приёмы, позволяющие единым методом решать задачи самой разнообразной природы.
Слайд 6Введение.
В алгебре экстремальные задачи встречаются в темах: «Линейная функция», «Рациональные дроби», «Неравенства»,

«Системы линейных уравнений и неравенств», «Квадратичная функция», «Последовательности и арифметическая прогрессия». На примере нескольких задач я расскажу о нахождении наибольшего и наименьшего значения в темах «Линейная функция», «Системы линейных неравенств и уравнений», «Рациональные дроби», «Квадратичная функция» и «Геометрия».
Слайд 7Линейная функция.
Наиболее простые, но не менее интересные задачи на экстремумы встречаются в

теме «Линейная функция». Вот одна из них:
Имеются ящики, в которые нужно упаковать 78 самоваров. Одни ящики вмещают 3 самовара, другие – 5 самоваров. Какое наименьшее количество ящиков нужно использовать, чтобы упаковать все самовары (недогрузка не допускается)?
Слайд 8Линейная функция.
Решение: Обозначим количество одних ящиков через х, а других – через у.

Тогда условие задачи даёт неопределённое уравнение вида 3х+5у=78. Пары чисел (26; 0), (21; 3), (16;6), (11; 9), (6; 12), (1; 15) являются решениями данного уравнения. (1;15) – оптимальное решение задачи.
Ответ: нужно использовать 16 ящиков.
Слайд 9Системы линейных уравнений и неравенств.
На соревнованиях каждый стрелок делал 10 выстрелов. За

каждое попадание он получал 5 очков, за каждый промах снималось 2 очка. Победителем считался тот, кто набрал не менее 30 очков. Сколько раз стрелок должен был попасть в мишень, чтобы быть в числе победителей?
Слайд 10Системы линейных уравнений и неравенств.
Решение: Обозначив число попаданий через х, число

промахов – через у, получим неравенство 5х-2у≥30. Составим систему 5х-2у≥30, 5х-20+2х≥30, х>7, х+у=10; у=10-х; у<3.
Решив систему получаем, что х={8,9,10}; y={2,1,0}. (8;2)–оптимальное решение.
Ответ: наименьшее число попаданий – 8.
Слайд 11Рациональные дроби.
На автомобиле новые шины. Шина на заднем колесе выдерживает пробег в

24000 км, а шина на переднем колесе– в16000 км. Какой максимальный путь можно совершить на этих шинах?
Решение: Износ шины на заднем колесе будет равен 1/16000 км, а износ шины на переднем колесе – 1/24000 км. Износ шин на обоих колёсах равен:1/16000+1/24000=1/9600. Максимальный путь равен 1/(1/9600)∙2=19200 (км).
Слайд 12Квадратичная функция.
А вот геометрическая задача на составле-ние квадратичной функции: В прямоугольный треугольник

с гипотенузой 16 см и углом 600 вписан прямоугольник, основание которого лежит на гипотенузе. Каковы должны быть размеры прямоугольника, чтобы его площадь была наибольшей?
Слайд 13Квадратичная функция.
Решение: AB=16 см. NК:КA=tg600=√3. По свойству пропорции получаем: КА=х√3/3. Треугольник АВС подобен

треугольнику МВL по двум углам. Составим отношение между сторонами треугольников: ВL:ВС=МL:АС. По теореме Пифагора ВС=8√3. Находим, что ВL=х√3. КL=16-4х√3:3. Площадь прямоугольника находим по формуле: S=x(16-4√3x/3)=-4√3х2/3+16х=-4√3:3(х-2√3)2 +16√3. Площадь будет наибольшей при х=2√3. Значит, КL=16(4∙2√3∙√3):3=8(см). Ответ: 2√3см и 8см.
Слайд 14Метод оценки.
Некоторые задачи на экстремумы решаются методом оценки. В методе оценки следует

коснуться неравенства Коши для нескольких переменных:
√а1а2…аn≤(а1+а2+…+аn)/n.
На одном из предприятий стоимость х деталей, изготовленных рабочим сверхурочно, определяется по формуле у=0,1х2+0,5х+2. Определите количество деталей, при котором себестоимость одной детали была бы наименьшей.
Слайд 15Метод оценки.
Решение: Найдём среднее арифметическое для 0,1х2, 0,5х и 2: (0,1х2+0,5х+2)/х=0,5+0,1х+2/х. Из трёх

величин одна постоянная (0,5), а две другие – переменные. Среднее геометрическое для переменных 0,1х и 2/х равно √0,2. Используя неравенство Коши для двух переменных получаем: 0,5+(2/х+0,1х)≥0,5+2√0,8; 0,5+(2/х+0,1х)≥0,5+√0,8. Левая часть неравенства принимает наименьшее значение равное 0,5+√0,8 .
Слайд 16Метод оценки.
Решаем уравнение 0,1х2-√0,8х+2=0; D=0,8-0,8=0; х=√0,8/0,2=√20. Но так как х –

это количество деталей, то х=4 или х=5.
Ответ: 4 или 5 деталей.
Слайд 17Геометрия.
Основу задач по геометрии на максимум и минимум составляют задачи на преобразование

плоскости. Основной задачей является старинная задача, написанная в I веке до н. э. Вот как она звучит:
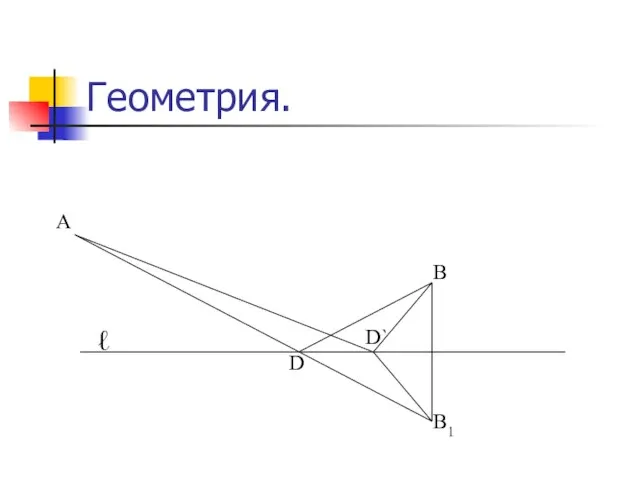
Даны две точки А и В по одну сторону от прямой ℓ. Требуется найти на ℓ такую точку D, чтобы сумма расстояний от А до D и от В до D была наименьшей.
Слайд 19Геометрия.
Решение: Пусть точка В1 – точка, симметричная точке В относительно прямой ℓ. Соединим

А с В1. Тогда точка D пересечения АВ1 с прямой ℓ – искомая. Действительно, для любой точки D`, отличной от D, имеет место неравенство: AD`+ D`B1>AB1 (т.к. в треугольнике сумма двух сторон больше третьей стороны); AD`+D`B>AD+DB.

















 Компьютер и здоровье глаз
Компьютер и здоровье глаз Пейзаж.Времена года
Пейзаж.Времена года Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Сложноподчиненное предложение. Повторение и обобщение изученного.
Сложноподчиненное предложение. Повторение и обобщение изученного. История радио и мобильной связи
История радио и мобильной связи А как ты знаешь физику?
А как ты знаешь физику? Презентация на тему Нефтяная промышленность
Презентация на тему Нефтяная промышленность  Изобразительное искусство барокко
Изобразительное искусство барокко Как начать бизнес в интернете?
Как начать бизнес в интернете? Sony Ericsson: Из VGA в HD
Sony Ericsson: Из VGA в HD Символика Краснодарского края
Символика Краснодарского края Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить.
Для умных женщин Одна супружеская пара поехала в выходные на озеро порыбачить. Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020
Бюджет для граждан по Решению Совета депутатов МО Александровский район от 23.12.2020 Children's behavior and its influence on their future acts
Children's behavior and its influence on their future acts РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Слова-паразиты, или экология речи
Слова-паразиты, или экология речи Иммунная система и канцерогенез
Иммунная система и канцерогенез  Подарки AI Journey. Предложения. Сберклауд
Подарки AI Journey. Предложения. Сберклауд Философские теории неврозов
Философские теории неврозов Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel)
Реализация и изучение игры «Жизнь» в среде электронных таблиц (MS Ecxel) Деструктивность учащегося и образовательной среды: точки соприкосновения
Деструктивность учащегося и образовательной среды: точки соприкосновения БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ
БАЛАНС-2W: ПОДГОТОВКА СПРАВКИ 2-НДФЛ Подготовка граждан к военной службе
Подготовка граждан к военной службе Ультразвуковые накладные расходомеры Flexim
Ультразвуковые накладные расходомеры Flexim Презентация для заказных проектов
Презентация для заказных проектов Поступление на государственную службу
Поступление на государственную службу Оценка достижений учащихся в разновозрастной группе
Оценка достижений учащихся в разновозрастной группе Grand Canyon National Park
Grand Canyon National Park