Применение генетических алгоритмов для генерации автоматов при построении модели максимального правдоподобия и в задачах управл

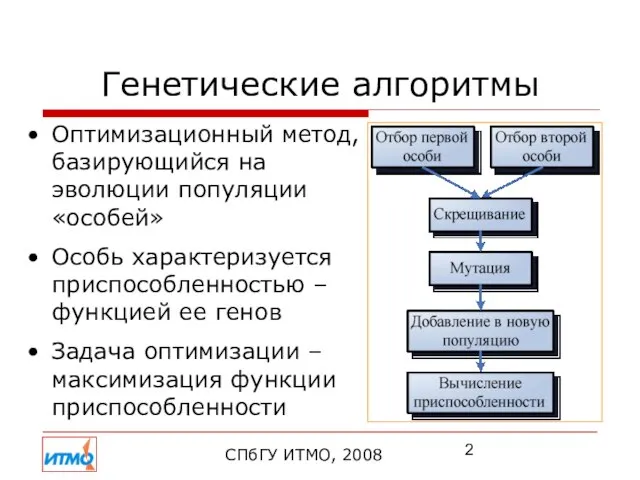
Генетические алгоритмы
Оптимизационный метод, базирующийся на эволюции популяции «особей»
Особь характеризуется приспособленностью – функцией ее генов
Задача оптимизации – максимизация функции приспособленности
СПбГУ ИТМО, 2008

Генетические алгоритмы и автоматы
Теория игр (итерированная дилемма узника)
Молекулярная биология (выбор праймера для ПЦР)
Роботехника (движение человекоподобного робота)
Зоология (искусственная этология)
Теория клеточных автоматов (DCT)
Регрессия (задача «о Флибах»)
Задача управления (задача об «Умном муравье»)
Задачи оптимизации
Проектирование логических схем
Распознавание изображений
Распознавание языков
СПбГУ ИТМО, 2008

В работе генетические алгоритмы и автоматы применяются для:
Построения моделей максимального правдоподобия одного класса. Задача: поиск ошибок в автоматах с помощью скрытых марковских моделей.
Решения нетривиальных задач оптимального управления. Задача: построение системы управления танком в игре Robocode.
СПбГУ ИТМО, 2008

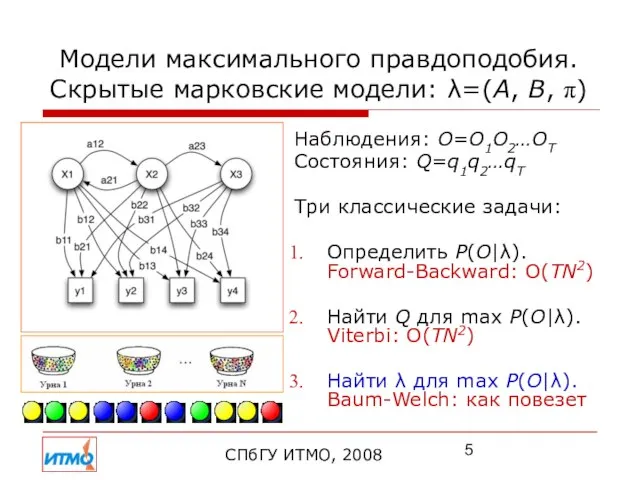
Модели максимального правдоподобия. Скрытые марковские модели: λ=(A, B, π)
Наблюдения: O=O1O2…OT
Состояния: Q=q1q2…qT
Три классические задачи:
Определить P(O|λ). Forward-Backward: O(TN2)
Найти Q для max P(O|λ). Viterbi: O(TN2)
Найти λ для max P(O|λ). Baum-Welch: как повезет
СПбГУ ИТМО, 2008

Недостатки алгоритма
Баума-Велша
СПбГУ ИТМО, 2008
Успешно применяется для решения актуальных задач – распознавание речи, предсказание структуры белка,…
Но имеются существенные недостатки:
Поскольку алгоритм градиентного спуска – застревание в локальных экстремумах
Как следствие – необходимость тщательного выбора начальных параметров

Поиск структуры графа – переходов с ненулевой вероятностью – с помощью генетических алгоритмов.
Won K., Hamelryck T., Prugel-Bennett A., Krogh A. Evolving Hidden Markov Models for Protein Secondary Structure Prediction / Proceedings of the IEEE. 2005.
СПбГУ ИТМО, 2008
Генетические алгоритмы для выбора начальных параметров

Предлагается выяснить когда BW алгоритм не работает без ГА и на сколько эффективно применение ГА в этом случае.
«Сильно детерминированные» модели
СПбГУ ИТМО, 2008
«Детерминированная» монетка:
Человек разумный:
Алгоритм Баума-Велша:
Для данного примера можно все поправить, но в общем случае не понятно, как это сделать.

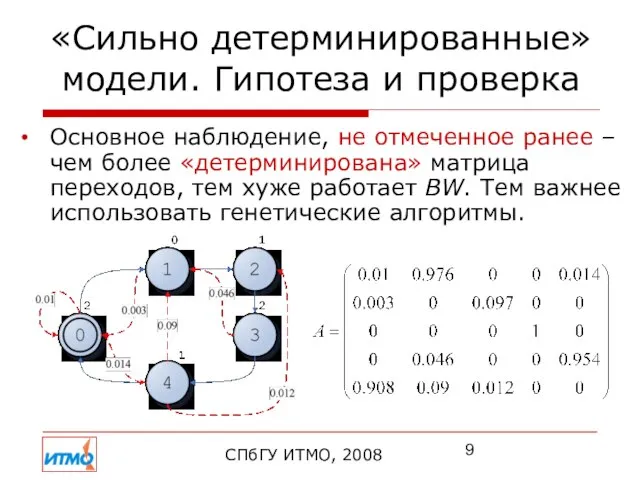
«Сильно детерминированные» модели. Гипотеза и проверка
СПбГУ ИТМО, 2008
Основное наблюдение, не отмеченное ранее – чем более «детерминирована» матрица переходов, тем хуже работает BW. Тем важнее использовать генетические алгоритмы.

Проверка гипотезы. Построение модели максимального правдоподобия
СПбГУ ИТМО, 2008
Один переход с большой вероятностью и не более двух – с малой. Граф связен.
N = 12, M = 3, чтобы задача была сложной:
пространство поиска (N2/2)N ≈ 2·1022
Набор из 10 входных последовательностей
Длина каждой – 200 элементов
Несколько десятков экспериментов

Типичный пример. Сравнение с алгоритмом случайного поиска
СПбГУ ИТМО, 2008
Исходная модель: -690
Оптимизированная модель: -678
Рассматриваемый метод: -675
Может быть задача не сложна?
Два алгоритма случайного поиска: -824

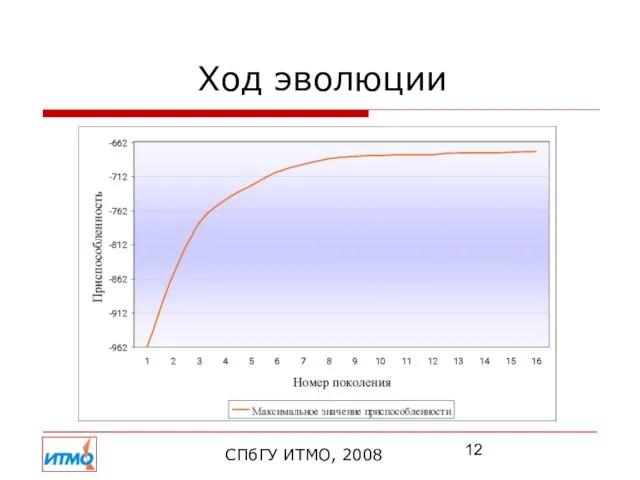
Ход эволюции
СПбГУ ИТМО, 2008

Есть ли практическая польза?
Поиск ошибок в автоматах с помощью скрытых марковских моделей
Методы:
Верификация
Тестирование
Преимущества предлагаемого метода:
не требует изменения структуры автомата
не требует добавления отладочной информации
СПбГУ ИТМО, 2008

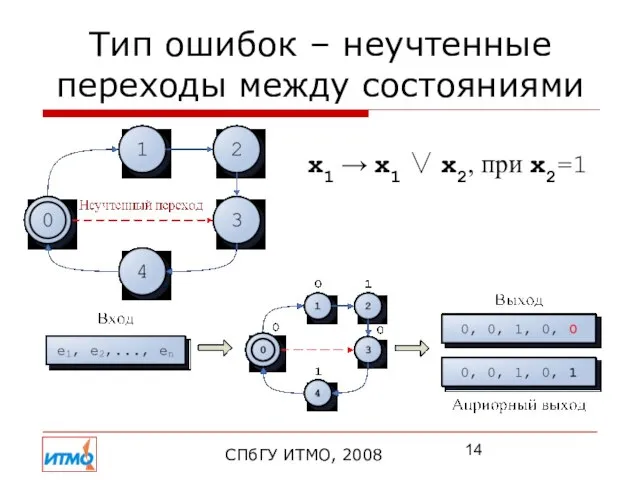
Тип ошибок – неучтенные переходы между состояниями
x1 → x1 ∨ x2, при x2=1
СПбГУ ИТМО, 2008

Результаты по первой части
Эмпирически установлена неприменимость BW алгоритма при построении моделей максимального правдоподобия некоторого класса HMM
Для указанного класса показана эффективность метода построения модели максимального правдоподобия, основанного на использовании генетических алгоритмов
Предложена и решена задача поиска ошибок одного типа в автоматах
СПбГУ ИТМО, 2008

Решение нетривиальных задач управления. Примеры и актуальность.
Беспилотным летательным аппаратом
Наземным средством передвижения
Различными системами этих средств (двигателем, системой стабилизации)
Бытовыми устройствами (лифтом, телевизором)
Транспортными потоками
Виртуальными объектами в играх и моделях (танком в игре Robocode, футболистами в виртуальном футболе)
СПбГУ ИТМО, 2008

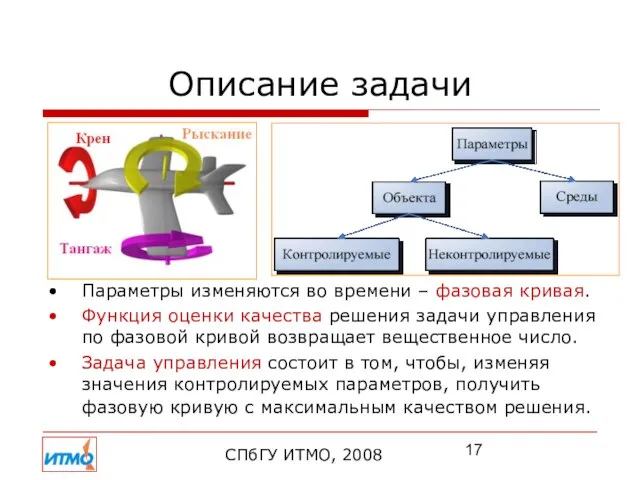
Описание задачи
СПбГУ ИТМО, 2008
Параметры изменяются во времени – фазовая кривая.
Функция оценки качества решения задачи управления по фазовой кривой возвращает вещественное число.
Задача управления состоит в том, чтобы, изменяя значения контролируемых параметров, получить фазовую кривую с максимальным качеством решения.

Формальная постановка задачи
СПбГУ ИТМО, 2008
Выделим n существенных для задачи управления вещественных параметров
Множество значений, принимаемых данными параметрами – Q = Rn
Временной интервал разбит на T мин. интервалов
Фазовая кривая φ – элемент QT, на момент t: φt
Качество управления – функция g: QT → R
Функция управления –
Вспомогательная функция
Начальные условия φ0 – элемент Rn
Задача управления –

Проблемы, возникающие при решении задачи
СПбГУ ИТМО, 2008
Зависимости между параметрами сложны. Задаются функцией h в неявном виде системой дифференциальный уравнений. Сложно решить аналитически.
Cложно найти вектор , так как он содержит большое число координат. Двухчасовой полет с интервалом 1 секунда – 7200 координат.
Каждая из координат вектора f – функция большого числа аргументов. Всего 10 параметров, на 85-ой минуте область определения – R85·60·10

Автоматный подход
СПбГУ ИТМО, 2008
При решении задачи управления часто можно выделить состояния, в которых может находиться объект управления
Количество различных координат функции управления полагается равным количеству состояний автомата
Координата функции управления управляет объектом исходя только из значений параметров в настоящий момент времени

Недостатки автоматного подхода
СПбГУ ИТМО, 2008
Задача эвристического определения конечного множества воздействий трудна
Сложность эвристического выбора компромисса между числом воздействий и размером пространства, на котором решается задача управления
Сложность эвристического построения графа переходов автомата, в частности, задания условий на переходах

Предлагаемый метод. Основная идея – применение ГА для автоматического построения автомата
СПбГУ ИТМО, 2008
Метод – программирование с экспрессией генов
Решение задачи управления – автомат – особь генетического алгоритма. Необходимо выбрать способ кодирования
Функция приспособленности ГА выражается через функцию g оценки качества решения. Определяется задачей
Генетические операции (мутация, скрещивание, отбор) – стандартные для программирования с экспрессией генов

Представление решения задачи управления в виде хромосомы
СПбГУ ИТМО, 2008
В состояниях:
Хромосома – набор N·(N-1) + m·N функций, отображающих из Q в R
На переходах:

Построение функции, отображающей из Rn в R
СПбГУ ИТМО, 2008
Функция – композиция базовых функции
Набор базовых функций: достаточно полный, но не слишком избыточный
Арифметические
Показательные
Логарифмические
Тригонометрические
Условные
Вероятностные

Апробация. Создание системы управления танком в игре Robocode
СПбГУ ИТМО, 2008

Параметры
СПбГУ ИТМО, 2008
x, y - координаты соперника относительно танка
dr - расстояние, которое осталось «доехать» танку
tr - угол, на который осталось повернуться танку
w - расстояние от танка до края поля
dh - угол между направлением на соперника и пушкой танка
GH - угол поворота пушки танка
h - направление движения соперника
d - расстояние между танком и соперником
e - энергия соперника
E - энергия танка

Контролируемые параметры и базовые функции
СПбГУ ИТМО, 2008
g – угол поворота пушки
p – энергия снаряда
d – длина перемещения
h – угол поворота танка
+(x, y)= x + y, ++(x, y, z) = x + y + z
n(x) = -x, *(x, y) = xy
**(x, y, z) = xyz, min(x, y)
if>(x, y, z, w) = x > y ? z : w
s(x) = (1 + e-x)-1

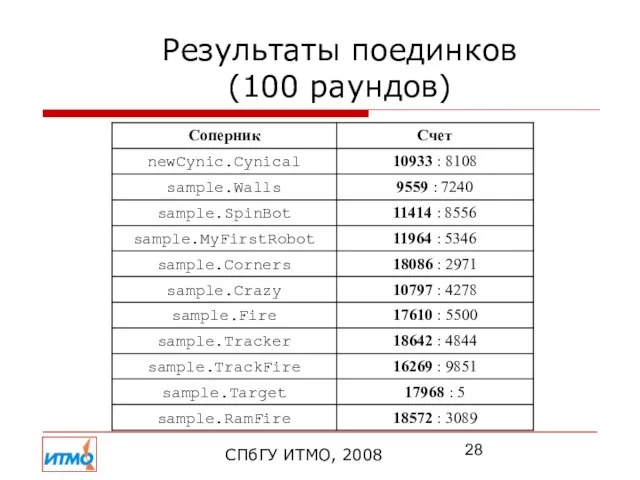
Результаты поединков
(100 раундов)
СПбГУ ИТМО, 2008

Заключение (результаты)
Эмпирически установлена неприменимость BW алгоритма при построении моделей максимального правдоподобия некоторого класса HMM
Для указанного класса показана эффективность метода построения модели максимального правдоподобия, основанного на использовании генетических алгоритмов
Предложена и решена задача поиска ошибок одного типа в автоматах
Предложен метод решения задач оптимального управления
Метод успешно опробован для построения системы управления танком в игре Robocode
СПбГУ ИТМО, 2008

Публикации
Государственный контракт: «Технология генетического программирования для генерации автоматов управления системами со сложным поведением»
Труды V Межвузовской конференции молодых ученых, 2008
Труды XII Всероссийской конференции «Фундаментальные исследования и инновации в технических Университетах», 2008
IV международная конференции по проблемам управления, 2009
XI Международной конференции по мягким вычислениям и измерениям, 2008
Конкурс грантов 2008 года для студентов и аспирантов ВУЗов и академических институтов
XV Всероссийская научно-методическая конференция «Телематика'2008»
На рецензию в журнал «Известия РАН. Теория и системы управления»
СПбГУ ИТМО, 2008